תַקצִיר
האגדה מספרת שהאדם הראשון ביוון העתיקה שגילה כי ישנם מספרים שלא ניתן לכתוב כשברים פשוטים, הושלך מעבר לסיפון של ספינה. מאות שנים מאוחר יותר, בזמן שאנו משתמשים באופן קבוע במספרים שלא ניתן לכתוב כשברים, המספרים האלה שכן ניתן לכתוב כשברים פשוטים נשארים כלים חזקים. מה גורם לשברים פשוטים להיות כל כך מיוחדים? נחקור כיצד אנו יכולים לזהות ייצוג עשרוני של שברים פשוטים, וכיצד אפשר להשתמש בשברים פשוטים כדי להעריך כל מספר ממשי באופן מדויק כרצונכם.
ביום שני בבוקר, חבר שלכם ג’ורדן בא אליכם ואומר: “אני חושב על מספר בין 1 ל-100.” בהיותכם סקרנים, אתם מנחשים שהוא חושב על המספר 43. “לא, זה נמוך מדי!” ג’ורדן מצהיר. “טוב, מה עם 82”? אתם שואלים. “גבוה מדי!”, ג’ורדן עונה. אתם ממשיכים לנחש. 60 הוא נמוך מדי. 76 הוא גבוה מדי. 70 הוא נמוך מדי. אתם מרגישים מרוצים כי אתם יודעים שאתם מתקרבים לתשובה, ואתם שואלים “מה עם 75?”. “הצלחתם!” ג’ורדן משיב, ואתם צועדים בניצחון ומתחילים את השיעור הראשון בבית הספר.
אולם אחרי השיעור אתם שוב נתקלים בג’ורדן, שמסתבר שחושב על דרכים לאתגר אתכם: למה לחשוב רק על מספרים חיוביים? מה אם גם תאפשרו מספרים שליליים? “כעת אני חושב על מספר בין 100- לבין ”100+ ג’ורדן אומר בשביעות רצון. אתם מחליטים לקחת את הפתיון, ובמהרה אתם מגלים שזה לא משנה הרבה את המשחק. אתם מנחשים, ועל ידי שינוי הניחוש למספר גבוה או נמוך יותר אתם מתקרבים עוד ועוד למטרה. אם המספר של ג’ורדן הוא 32-, וכבר הבנתם ש-33- הוא נמוך מדי וש-31- הוא גבוה מדי, אז אתם יודעים שהתשובה היא 32-. אולם, אז אתם מבינים: אין שום דבר מיוחד ב-100- וב-100! אם תתחילו עם מספר בין 1,000- לבין 1,000, אתם יודעים שבסופו של דבר תנחשו את המספר הנכון אפילו אם זה ידרוש יותר ניחושים. אתם צועדים לשיעור השני בבית הספר בצעד מנצח, בטוחים שתהיו מוכנים לאתגר הבא של ג’ורדן.
אולם במהלך השיעור, אתם מבינים שהנחתם שג’ורדן תמיד יבחר מספר שלם. מה עם שברים גם מותרים? נניח שג’ורדן יבחר מספר בין 0 לבין 1, למשל 3/22. אתם צריכים לנחש מספר שנמצא בין 0 ל-1. אתם מתחילים בדיוק באמצע ואתם מנחשים 1/2. ג’ורדן אומר לכם שהניחוש שלכם גבוה מדי, אז אתם יודעים שהתשובה היא איפשהו על הקו שבין 0 לבין 1/2. אתם מנחשים שוב באמצע: 1/4. ג’ורדן אומר ש-1/4 עדיין גבוה מדי, אז אתם יודעים שהתשובה חייבת להיות על הקו שבין 0 לבין 1/4. אתם ממשיכים עם האסטרטגיה שלכם, ואתם מנחשים 1/8, 3/16, 5/32, 9/64, וכדומה. ייצוג אחד של המשחק הזה מוצג באיור 1. נראה שזה לוקח זמן רב! האם אי פעם תנחשו את המספר הנכון? אולי יעזור לכם שינוי אסטרטגיה. האם אתם תיתקעו בניחושים לעד?
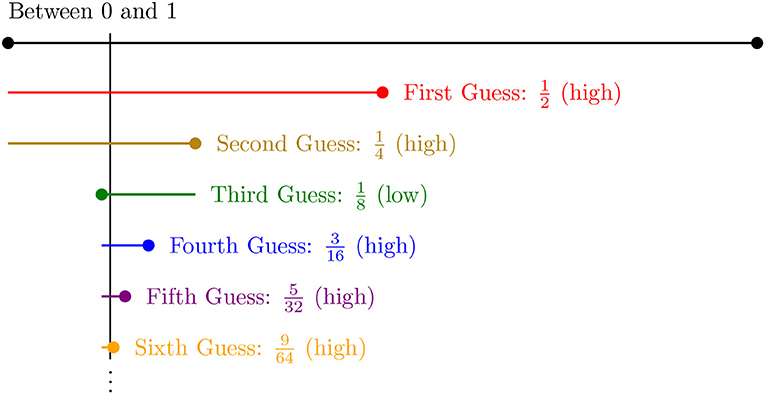
- איור 1 - משחק ניחוש המספרים.
- חבר שלכם ג’ורדן מבקש מכם לנחש מספר בין 0 ל-1. בכל ניחוש, אתם חוצים את הטווח שבו המספר של ג’ורדן עשוי להיות. הנקודה בסוף כל קו היא הניחוש שלכם. מיקום המספר שאתם מנסים לנחש, 3/22, מסומן על ידי הקו השחור האנכי.
אסטרטגיה חדשה: ייצוגים עשרוניים
בואו נסתכל על המספרים האלה באופן שונה, ונחשוב עליהם כמספרים עשרוניים. אנו יכולים להפוך שבר למספר עשרוני על ידי חלוקת המונה במכנה. ככה זה עובד עבור השבר 7/16:
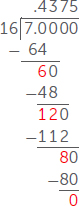
בצעד הראשון של החלוקה, אנו שואלים כמה פעמים 16 נכנס ב-70 (למעשה, אנו שואלים כמה פעמים 1.6 נכנס ב-7.0, אולם התשובה זהה לכמות הפעמים ש-16 נכנס ב-70). מאחר ש- 16 x 4 = 64, אנחנו רושמים 4 מעל ל-0 ב-7.0. לאחר מכן, אנו מחסירים 64 מ-70 ומקבלים את המספר הנותר 6. במקרה הזה, 6 נקרא שארית.
בצעד הבא, אנו מביאים 0 נוסף מ-7.00. אנחנו שואלים כמה פעמים 16 נכנס ב-60. מאחר ש-16 x 3 = 48, אנחנו כותבים 3 מעל ל-0 השני. לאחר מכן, אנו מחסירים 48 מ-60 ומקבלים 12.
אנו ממשיכים עם התהליך הזה, ומורידים אפסים אחרי כל שארית ושואלים כמה פעמים 16 נכנס במספר שנותר. לאחר שעשינו את זה ארבע פעמים, אנו מגיעים לשארית 0, שבתוכה המספר 16 נכנס אפס פעמים. בנקודה הזו, סיימנו עם החלוקה הארוכה שלנו ואנו יכולים לומר ש-7/16 = 0.4375. אם אתם משחקים במשחק ניחוש מספרים, אתם יכולים להגיע לגרסה העשרונית הזו של 7/16 בכמה צעדים קצרים. הטבלה למטה מראה דרך אפשרית שבה זה יכול לקרות. בטבלה, H מסמן שהניחוש שלכם היה גבוה מדי, ו-L מסמן שניחוש שלכם היה נמוך מדי.
| .4375 | .438 | .437 | .435 | .43 | .44 | .45 | .4 | .2 | .5 | guess |
| CORRECT! | H | L | L | L | H | H | L | L | H | response |
מאחר שהייצוג העשרוני של 7/16 הוא מספר סופי, אתם יכולים לנחש את המספר המדויק על ידי ניחוש של ספרה אחת בכל פעם במספר העשרוני. האם זה קורה עבור כל השברים? בואו נסתכל על המספר העשרוני 3/22.
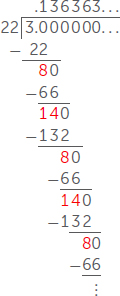
אם נעקוב אחרי אותו תהליך החלוקה, נקבל 1 למעלה עם שארית של 8, 3 למעלה עם שארית של 14, 6 למעלה עם שארית של 8, 3 למעלה עם שארית של 14... אבל רגע! כבר ראינו את השאריות האלה, ואנו יודעים שהמספר הבא למעלה הוא 6 עם שארית 14 שוב. כשנמשיך לחלק, שתי השאריות של 8 ו-14 יתנו לנו ספרות חוזרות של 3 ו-6 בייצוג העשרוני של 3/22. משמעות הדבר היא שאם תנסו לנחש את המספר 3/22 על ידי ספרה עשרונית אחת בכל פעם, אתם תצטרכו להמשיך לנחש לעד!
מספרים רציונליים
כל המספרים שהסתכלנו עליהם עד כה נקראים מספרים רציונליים. מספר רציונלי הוא כל מספר שאנו יכולים לכתוב כשבר a/b של שני מספרים שלמים (חיוביים או שליליים), a ו-b. משמעות הדבר היא שהמספר 2/5 הוא מספר רציונלי מאחר ש-2 ו-5 הם מספרים שלמים. כמו כן, 3 הוא מספר רציונלי מאחר שניתן לכתוב אותו כ- 3/1, ו-4.5 הוא מספר רציונלי מאחר שניתן לכתוב אותו כ- 4.5 = 9/2. אפילו אם לא נכתוב את 3 ואת 4.5 כשברים, הם מספרים רציונליים מאחר שאנו יכולים לכתוב שבר ששווה לכל אחד מהם.
ראינו שלחלק מהמספרים הרציונליים, כמו למשל 7/16, יש ייצוגים עשרוניים סופיים. אנו קוראים למספרים האלה שברים מסתיימים. למספרים רציונליים אחרים, כמו למשל 3/22, יש ייצוגים עשרוניים שממשיכים לעד. אולם אנו יודעים שאפילו הייצוגים העשרוניים שלא מסתיימים בכל זאת חוזרים על עצמם, אז אנו קוראים להם שברים מחזוריים.
עבור כל מספר רציונלי a/b, השאריות היחידות שאנו יכולים לקבל הן המספר 0, 1, 2, ...3, b-2, b-1. לדוגמה, כשכתבנו את הייצוג העשרוני של 3/22, האפשרויות היחידות שהיו לנו לשאריות היו 0, 1, 2, ...3, 20, 21. מאחר שישנו רק מספר סופי של מספרי שאריות, השאריות חייבות לחזור על עצמן בסופו של דבר. זה נכון לכל השברים העשרוניים שאינם מסתיימים. אף על פי שישנה תבנית חוזרת לייצוג העשרוני של השברים האלה, לעולם לא ננחש את המספר המדויק במשחק ניחוש המספרים אם ננחש ספרה עשרונית אחת בכל פעם, מאחר שהספרות העשרוניות ממשיכות לעד. איננו יכולים להגיד כמות אינסופית של ספרות!
אנו יכולים ללכת בכיוון השני ולשנות את השברים העשרוניים לשברים פשוטים! כשיש לנו ייצוג עשרוני של שבר מסתיים, כמו למשל 4.132, אנו יכולים לשנות אותו לשבר פשוט באמצעות ערך המיקום. ה-2 של המספר 4.132 נמצא במיקום האלפים, אז 4.132 = 4132/1000. אם אנחנו מתחילים עם שבר עשרוני מחזורי, נצטרך לעבוד יותר כדי למצוא את השבר הפשוט התואם שלו. לדוגמה, חשבו על 0.353535….. קראו למספר הזה A. החלק החוזר 35 מכיל שתי ספרות, אז אנחנו מכפילים את A ב-100 כדי להזיז את הנקודה העשרונית בשני מקומות. זה נותן 100A = 35.353535…. שימו לב שכל המיקומים העשרוניים ב-A וב-100A תואמים זה לזה. אנו נחסר את A מ-100A כדי לקבל 99A. לאחר מכן, נחסיר את הספרות העשרוניות. ה-0.353535… זהה בשני המספרים, ולכן הוא מתבטל בהפרש. אם כן, אנו נשארים עם מספרים שלמים בלבד!
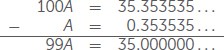
יש לנו 99A = 35, ולכן אנו מחלקים ב-99 ומקבלים A=35/99. עבור כל ייצוג עשרוני של שבר מחזורי, אנו יכולים להשתמש באותו התהליך כדי למצוא את השבר התואם. אנחנו מכפילים ב-10, 100, 1000, או בכמה שנדרש כדי להזיז את הנקודה העשרונית רחוק מספיק כך שהספרות העשרוניות יסתדרו במספר המקורי ובמספר המוכפל. לאחר מכן אנו מחסירים ומשתמשים בתוצאה כדי למצוא את השבר התואם. משמעות הדבר היא שכל ייצוג עשרוני של שבר מחזורי הוא מספר רציונלי!
מספרים אי-רציונליים
מה עם יש לנו ייצוג עשרוני שלא מסתיים, אולם הספרות שלו לא חוזרות על עצמן? לדוגמה, תסתכלו על המספר 0.101001000100001….. במספר הזה, אנו מגדילים את כמות האפסים בין כל זוג של אחדות, ראשית יש לנו אפס אחד, אחריו שני אפסים, אחריו שלושה אפסים, וכדומה. המספר הזה לא יכול להיות רציונלי מאחר שאנו יודעים שייצוג עשרוני למספר רציונלי הוא מסתיים או מחזורי. זו דוגמה למספר אי-רציונלי. מספר אי-רציונלי הוא כל מספר שאיננו יכולים לכתוב כשבר של מספרים שלמים. ככל הנראה שמעתם על המספר האי-רציונלי המפורסם פיי, כאשר π = 3.14159…, אשר נותן את היחס בין היקף המעגל לבין קוטרו. בעוד שזהו יחס, לפחות היחס שבין ההיקף לקוטר המעגל, זה אינו מספר שלם, ולכן π אינו מספר רציונלי. מספר אי-רציונלי אחר הוא המספר 414211.... = , שהוא אורכו של האלכסון של ריבוע שאורך צלעו הוא 1.
אם נחזור למשחק שלנו, כל המספרים הרציונליים והאי-רציונליים יחד ממלאים את קו המספרים שלנו בין 0 ל-1. נניח שחבר שלכם ג’ורדן יכול לבחור כל מספר בין 0 ל-1, ובוחר מספר אי-רציונלי שאתם צריכים לנחש. ככל הנראה יהיה לכם קשה לנחש את המספר המדויק! ממש כמו במקרה של הייצוג העשרוני המחזורי של 3/22, אתם לא יכולים לומר כמות אינסופית של ספרות, ולכן המשחק הזה נראה לא הוגן.
בואו נשנה את המשחק כך שתוכלו לנצח! ג’ורדן בוחר שלושה דברים: מספר שאתם צריכים לנחש; טווח של מספרים שבו המספר נמצא, וכמה קרוב הניחוש שלכם צריך להיות. עם החוקים האלה, ג’ורדן בוחר את המספר π ואומר לכם “אני חושב על מספר בין 2 ל-10. תנסו לנחש מספר בטווח של 0.01 מהמספר שלי”. במקרה הזה, המשחק יכול ללכת ככה:
| 3.14 | 3.12 | 3.15 | 3.1 | 3.2 | 3.5 | 3 | 4 | 6 | guess |
| !! π within 0.01 of | L | H | L | H | H | L | H | H | response |
בגרסה החדשה הזו של המשחק, אפילו אם ג’ורדן משנה את מידת הקרבה שאתם צריכים לנחש, תמיד תוכלו בסופו של דבר להגיע למרחק הזה מהמספר π. אתם רק צריכים להצליח לקבל את החלק השלם של המספר, וחלק מסוים מהספרות העשרוניות. לדוגמה, בטווח של 0.1 מ- π, אתם רק צריכים לנחש נכון את הספרה העשרונית הראשונה. כדי להיות בטווח של 0.01 מ- π, אתם צריכים לנחש נכון את שתי הספרות העשרוניות הראשונות. כדי להיות בטווח של 0.001 מ- π, אתם צריכים לנחש נכון את שלוש הספרות העשרוניות הראשונות. לא משנה כמה קרוב הניחוש שלכם צריך להיות, אתם יכולים לנצח במשחק החדש הזה על ידי ניחוש ספרה במיקום עשרוני אחד בכל פעם, עד שניחשתם נכון מספיק ספרות עשרוניות.
כפי שראינו קודם לכן, כל שבר מחזורי הוא מספר רציונלי. אם נשתמש בתהליך הזה כדי להתקרב עוד ועוד למספר אי-רציונלי, באמצעות ניחוש עוד ועוד ספרות עשרוניות של המספר, אנו יכולים לקבל מספר רציונלי שהוא קרוב כרצוננו למספר היעד האי-רציונלי שלנו. במשחק שלנו, משמעות הדבר היא שלא משנה מהו המספר האי-רציונלי שג’ורדן בוחר, אתם תמיד יכולים למצוא מספר רציונלי שיתאים לדרישות. במשחק הזה, אתם תמיד יכולים לנצח!
מסקנות
הסיבה לכך שזה קורה היא שקבוצת המספרים הרציונליים היא קבוצה צפופה ביחס למספרים ממשיים. זה אומר שבין כל שני מספרים רציונליים שונים, אנו יכולים למצוא מספר רציונלי נוסף. מאחר שלמספרים רציונליים יש את התכונה הזו, אנו יכולים להעריך כל מספר אי-רציונלי באמצעות מספר רציונלי. קירוב של מספר אי-רציונלי באמצעות מספר רציונלי הוא מה שאתם עושים במשחק החדש כשג’ורדן בוחר מספר אי-רציונלי.
אולם מדוע שאי פעם נצטרך להעריך מספר אי-רציונלי באמצעות מספר רציונלי? נניח שאתם בונים מסגרת עץ עבור מיטת גינה משולשת בגודל של חצי מהריבוע באיור 2 (אורכו של צלע הריבוע היא 1 מטר). אתם צריכים לחתוך חתיכת עץ שתהיה באורך של מטרים. כיצד תמדדו את האורך הזה? מאחר ש- הוא מספר אי-רציונלי, אינכם יכולים להשתמש בסרט המדידה שלכם כדי למדוד אותו במדויק! במקום זאת, אתם צריכים לבחור מספר רציונלי מקורב ל-. אתם יכולים לבחור את מספר הספרות העשרוניות שתכללו בייצוג שלכם, כדי לקבל את חתיכת העץ באורך קרוב כרצונכם ל-, באותו האופן שאתם בוחרים את המספר הרציונלי קרוב כרצונו של ג’ורדן למספר האי-רציונלי שהוא בוחר.
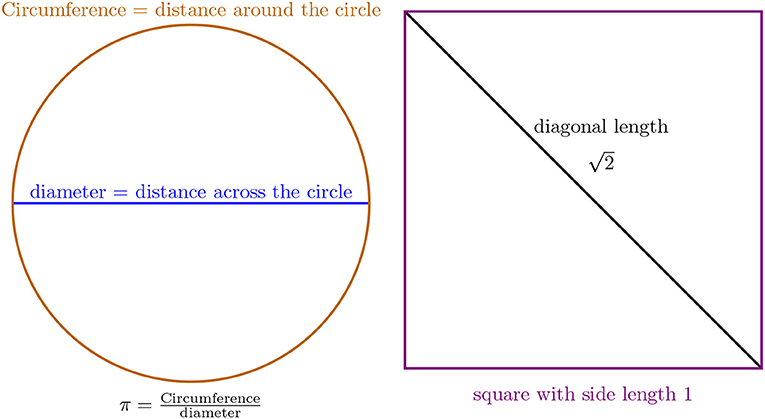
- איור 2 - שני מספרים אי-רציונליים שאנו פוגשים בגיאומטריה.
משמאל: π הוא ערכו של היחס שבין היקף המעגל לבין קוטרו. מימין: הוא אורכו של אלכסון של ריבוע שאורך צלעו היא 1.
הערכת מספרים אי-רציונליים באמצעות מספרים רציונליים היא כלי חזק מאוד לביצוע חישובים; למדידת חומרים בבנייה, ולהרבה יישומים אחרים. העובדה שקבוצת המספרים הרציונליים צפופה ביחס למספרים הממשיים היא שמאפשרת לנו להשתמש בכלי הזה!
מילון מונחים
מספר רציונלי (Rational Number): ↑ מספר ממשי שניתן לכתוב כשבר של שני מספרים שלמים. ייצוגים עשרוניים למספרים רציונליים יכולים להיות או שברים מחזוריים או שברים מסתיימים.
שבר מסתיים (Terminating Decimal): ↑ ייצוג עשרוני שיש לו מספר סופי של ספרות שאינן אפס. לדוגמה, 3.125 הוא שבר מסתיים.
שבר מחזורי (Repeating Decimal): ↑ ייצוג עשרוני שבו הספרות חוזרות על עצמן. כלומר, בסופו של דבר הספרות נכנסות לתבנית שחוזרת על עצמה לעד. לדוגמה, 0.3333… ו-3.125353535… הם שברים מחזוריים.
מספר אי-רציונלי (Irrational Number): ↑ מספר ממשי שלא ניתן לכתוב כשבר של שני מספרים שלמים. ייצוגים עשרוניים למספרים אי-רציונליים הם אינסופיים ואינם חוזרים על עצמם.
קבוצה צפופה (Dense): ↑ קבוצת מספרים היא צפופה ביחס למספרים הממשיים אם לכל שני מספרים ממשיים שונים, ישנו מספר בקבוצה שנמצא ביניהם. לדוגמה, קבוצת המספרים השלמים אינה צפופה ביחס למספרים הממשיים מאחר שאין מספר שלם בין 2.1 ל-2.2.
הצהרת ניגוד אינטרסים
המחברים מצהירים כי המחקר נערך בהעדר כל קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.
