Abstract
Have you ever been in the playground playing a game of naming the biggest number you can think of? How quickly does someone say “infinity?” Then the next person says, “infinity plus one,” and the game never seems to stop. But is infinity plus one really bigger than infinity? Can we do maths with infinity? Georg Cantor (1845–1918) was one of the first mathematicians who studied infinity. He came up with different examples where infinity appears in mathematics. He also discovered that there were different types of infinity. This made other mathematicians dismiss his work as wrong and confusing. It was David Hilbert who made infinity understandable with his Infinity Hotel in 1924. His explanation was a story of a hotel that even when it was full, had space for more guests. This article tries to explain infinity in a similar way.
Introduction: Cardinality, Which Means Counting
Infinity is strange and confused mathematicians to start with. It comes up naturally when we first learn that counting goes on forever. To help us understand the strange behavior of infinity, mathematicians went back to the basic and tried to define what it means to count.
Imagine you have a bag full of sweets. You cannot see in the bag, but you want to know how many sweets you have. The best way to do that would be to reach in the bag, pull out the first sweet and say “one.” Next, you would pull out the second sweet and say “two.” You would keep doing this until the bag is empty. The last number you say is how many sweets you have in your bag. This is how we learn to count, no matter what objects you have in your bag.
Definition: Cardinality
The cardinality of a bag of objects1 is the number of objects in the bag. This can be determined by counting how many objects are there in the bag.
For example, a bag with three sweets in it has cardinality three. A bag with one sweet, one robot, and a pencil also has cardinality three. It does not matter what the objects are, just the number matters. The bag could contain more abstract objects, for example a bag with the numbers 1, 2, and 3 in it.
Two bags with the same cardinality have the same number of objects in them. We can pair up the objects in both bags without either bag having something left over. This gives us another way of counting objects. If we know the cardinality of one bag, but not of another, we can check if we can pair up the objects in both bags.
For example, you have a bag of sweets, but you do not know how many sweets are in the bag. This time, you also have eight friends. If you can give exactly one sweet to each of your eight friends, with no sweets leftover, then the cardinality of the bag of sweets is eight. If at least one friend does not get a sweet, then the cardinality of the bag is less than eight. If at least one sweet is leftover, then the cardinality of the bag is more than 8.
Countably Infinite
Imagine now a bag containing all the positive numbers: 1, 2, 3, 4, and so on. We use the symbol ℕ to mean this bag2. What is the cardinality of this bag, ℕ? It clearly does not have cardinality 4, as ℕ contains at least five objects, namely the numbers 1, 2, 3, 4, and 5. The same logic works for any number. Pick any number, say n, then the bag ℕ contains at least n + 1 objects, namely the numbers 1, 2, 3, …, n and n + 1. This shows the cardinality of ℕ is not a number, and we say ℕ is countably infinite3.
Definition: Countably infinite
A bag of objects is countably infinite if it has the same cardinality as ℕ. In other words:
- The bag contains infinitely many objects, so we can forever pick something out of it.
- We can pair each object in the bag with a unique positive whole number (another way of saying, we can count the objects).
Example 1: Even numbers
Imagine two bags. One with all the positive numbers, called ℕ, and one with all the positive even numbers, called 2ℕ. It would seem natural to think that there are more positive numbers than there are positive even numbers. But we will show that you can pair every even number to exactly one number, in such a way that there are no leftovers. This will show that ℕ and 2ℕ have the same cardinality.
Before we do this, we need a way to tell apart the numbers that we grab from the bag ℕ, and the even numbers that we grab from the bag 2ℕ. We add “th” to the end of any number coming from bag ℕ. Examples:
- 6th is a number from ℕ and 6 is an even number from 2ℕ.
- 7th is a number from ℕ, and since 7 is not even, it is not in our bag 2ℕ.
The way to pair the numbers from ℕ and 2ℕ is to say: the nth number is paired with the even number 2n. Examples:
- The 4th number is paired with the even number 8.
- The 5th number is paired with the even number 10.
- The 57th number is paired with the even number 114.
We see that every number from ℕ is paired up with an even number. We also see that every even number is paired up with a number, as the even number n is paired up with the (n ÷ 2)th number. This means we have paired up every number in ℕ with a number in 2ℕ, and there are no leftovers (Figure 1). Hence, ℕ and 2ℕ have the same cardinality. The bag of even numbers is countably infinite. This means that there are the same amount of positive numbers as there are positive even numbers.
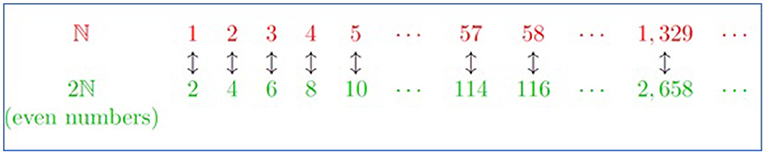
- Figure 1 - Each number from ℕ can be paired with a single even number from 2ℕ.
- So there is as many numbers as there is even numbers.
Adding One To Infinity
Example 2: Imagine two bags, both containing all the positive numbers. Both bags currently have the same number of objects (they are both countably infinite). Now add one object, the letter A, to the second bag. Does the second bag have more objects than the first bag? No, in fact they have the same number of objects.
As before, we call the first bag ℕ, and we will add “th” to the end of any number in that bag. The second bag, which contains A, 1, 2, 3, and so on, will be called as ℕ0. We pair every object in ℕ with a single object in ℕ0 using the two rules:
- The 1th number is paired with the letter A from ℕ0.
- When n is not one, the nth number is paired with the number n – 1 from ℕ0.
Examples
- The 1th number is paired with the letter A.
- The 5th number is paired with the number 4.
- The 30th number is paired with the number 29.
This way, every object in ℕ is paired with a single object in ℕ0. Therefore, both bags have the same cardinality, so the same number of objects.
This logic works for any number of things we add to the bag ℕ. So, no matter how many finite things we add to ℕ, the bag is still countably infinite and contains the same number of objects.
Adding Infinity to Infinity
Example 3: We have seen that a bag containing all the positive numbers is countably infinite. By the same logic, a bag containing all the negative numbers is also countably infinite. What if we put, in one bag, all the positive numbers, all the negative numbers, and 0? Is this bag bigger than the bag ℕ?
We will use the symbol ℤ to mean the bag containing all the numbers (positive, negative, and zero)4. To pair up the numbers in ℕ with the numbers in ℤ, we need to use more complicated rules.
- If n is odd, then the nth number is paired with the number (n – 1) ÷ 2 in ℤ.
- If n is even, then the nth number is paired with the number–(n ÷ 2) in ℤ.
Examples:
- 4 is even and 4 ÷ 2 = 2. So, the 4th number is paired up with the number –2.
- 5 is odd, so we do 5 – 1 = 4 and 4 ÷ 2 = 2. So, the 5th number is paired up with the number 2.
- The 24th number is paired up with the number –12.
- The 57th number is paired up with the number 28.
Again, we have paired every object in ℕ with an object in ℤ (Figure 2). This means that they have the same cardinality. Hence, ℤ is countably infinite. There are as many numbers (positive and negative) as there are positive numbers.

- Figure 2 - Each number from ℕ can be paired with a single number from ℤ.
- So there is as many numbers as there is positive and negative numbers.
Subtracting from Infinity
We have seen that adding one or infinitely many objects to a bag that is countably infinite does not make the bag any bigger (see Example 3). But, what happens if we start removing objects from a countably infinite bag?
Example 4: Imagine the bag containing all the positive numbers and remove the number 1 from it. We will call this bag ℕ1. We show that the bag ℕ1 is countably infinite by pairing every element of ℕ1 with an element of ℕ. As before, we will add “th” to the end of any number coming from ℕ. We will pair the nth number (from ℕ) with the number n + 1 from ℕ1.
Examples
- The 1th number is paired with the number 2.
- The 5th number is paired with the number 6.
- The 30th number is paired with the number 31.
Every object in ℕ is paired with a single object in ℕ1. Therefore, both bags have the same cardinality, so the same number of objects.
This logic works for any number of things we remove from the bag ℕ. No matter how many finite things we take away from ℕ, the bag is still countably infinite and still contains the same number of objects.
Now, what if we removed countably infinitely many objects? Then the answer depends on what we remove.
Example 5: We know that the positive even numbers are countably infinite (see Example 1). Imagine a bag that contains all the positive numbers, and remove from that bag all the even positive numbers. All that is left in the bag are the positive odd numbers. In the same way that the even numbers are countably infinite, the odd numbers are also countably infinite (to see this, we pair the nth number with the 2n — 1 odd number, see Figure 3).

- Figure 3 - Each number from ℕ can be paired with a single odd number.
- So there is as many numbers as there is odd numbers.
In this case, starting with a countably infinite bag and removing countably infinite objects from it, we are still left with countably infinitely many objects, or in other words, a countably infinite bag.
Example 6: Imagine a bag with all the positive numbers in it, like the bag ℕ. Imagine we remove all the numbers bigger than 1. What we have removed from ℕ is the bag ℕ1 (see Example 4). What we are left with is a bag containing the number 1. A bag containing just the number 1 has cardinality 1.
In this case, starting with a countably infinite bag and removing countably infinite objects from it, we are left with a single object.
Conclusion
This article shows some of the strange behaviors of infinity. The examples above show that we cannot work with infinity as if it is a number. When we perform addition and subtraction, infinity behaves differently than numbers do.
While this strangeness confused mathematicians at first, by going back to basic, they managed to understand infinity. This has been repeated throughout the history that the concepts that were once mysterious were finally understood by being careful with definition.
Glossary
Cardinality: ↑ The number of objects in a bag.
ℕ: ↑ The “natural numbers”, the bag that contains all the positive numbers, 1, 2, 3, 4 and so on.
Countably Infinite: ↑ A bag that contains infinitely many objects, but we can still count the objects. In other words, a bag with the same cardinality as ℕ.
ℤ: ↑ The “integers”, the bag that contains all the negative numbers, zero and all the positive numbers.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnotes
1 ↑ In maths, we use the word set to mean a bag of objects.
2 ↑ ℕ is a bold N. It stands for “natural numbers.”
3 ↑ We use the adjective countably, as there are other types of infinity that are infinitely bigger than countable infinite.
4 ↑ This is a bold Z, and stands for “zahlen,” which is German for “numbers.”
