תַקצִיר
האם כשהייתם קטנים, שיחקתם משחק שבו כל אחד צריך להגיד את המספר הגבוה ביותר שהוא יכול לחשוב עליו? כמה מהר מישהו אומר “אֵינְסוֹף”? ואז, מישהו אַחֵר אומר: “אינסוף ועוד אחת”, ונראה שהמשחק לעולם לא יסתיים. האם “אינסוף ועוד אחת” באמת גדול יותר מ“אינסוף”? האם אפשר לפתור תרגילי חשבון עם “אינסוף”? גיאורג קנטור (1918-1845) היה אחד המתמטיקאים הראשונים שחקר את המושג “אינסוף”. הוא חשב על דוגמאות שונות שבהן ה“אינסוף” מופיע במתמטיקה. הוא גם גילה שיש סוגי “אינסוף” שונים. הדבר גרם למתמטיקאים אחרים להתייחס אל עבודתו בזלזול, כעבודה שגויה ומבלבלת. בשנת 1924, היה זה דויד הילברט שגרם ל“אינסוף” להיות מובן, בעזרת “פָּרָדוֹקְס הַמָּלוֹן האינסופי”. ההסבר שלו היה סיפור על מלון שגם כאשר הוא בתפוסה מלאה יש בו מקום לאורחים נוספים. במאמר זה אנסה להסביר את המושג “אינסוף” בצורה דומה.
הקדמה: קרדינליוּת, שפירושה סְפִירָה
המושג “אינסוף” הוא מוזר, ובלבל מתמטיקאים שעסקו בו. הבנתו מושׂגת באופן טבעי כאשר אנו מבינים לראשונה שאפשר להמשיך ולספור לָנֶצַח. כדי לעזור לנו להבין את ההתנהגות המוזרה של ה“אינסוף”, חזרו מתמטיקאים ליסודות, וניסו להגדיר מהי משמעות פעולת הספירה.
תארו לעצמכם שיש לכם תיק מלא בממתקים. אינכם יכולים לראות את תוכן התיק, אבל ברצונכם לדעת כמה ממתקים יש לכם. הדרך הטובה ביותר לעשות זאת היא להושיט יד לתוך התיק, להוציא את הממתק הראשון ולומר: “אחת”. אחר כך, להוציא ממתק שני ולומר: “שתיים”. תמשיכו לעשות זאת, עד שהתיק יתרוקן. המספר האחרון שתאמרו הוא מִנְיָן הממתקים שהיו בתיק. כך אנו לומדים לספור, ולא משנה מהם הפריטים שנמצאים בתיק שלכם.
הגדרה: קרדינליוּת
הקַּרְדִּינָלִיּוּת של תיק מלא פריטים1 היא מִנְיָן הפריטים שיש בתיק. זאת אפשר לקבוע על-ידי ספירת מִנְיָן הפריטים הנמצאים בתיק.
למשל, הקרדינליות של תיק המכיל שלושה ממתקים היא 3. גם הקרדינליות של תיק שבתוכו יש ממתק אחד, רובוט אחד ועיפרון אחד היא 3. לא חשוב מהם הפריטים שבתיק, רק המספר חשוב. התיק יכול להכיל פריטים מופשטים יותר, למשל: תיק המכיל את המספרים 1, 2 ו־3.
שני תיקים שיש להם את אותה קרדינליות יכילו את אותו מִנְיָן פריטים. אנו יכולים לסדר את הפריטים מִשְּׁנֵי התיקים בזוגות, בלי שיישאר פריט כלשהו באחד התיקים. זוהי דרך נוספת לספור פריטים. אם אנו יודעים מהי הקרדינליות של תיק אחד, אבל לא את הקרדינליות של התיק האחר, אנו יכולים לבדוק אם אפשר לסדר את הפריטים בזוגות, כך שבכל זוג יש פריט אחד מכל תיק.
למשל, יש לכם תיק המכיל ממתקים, אבל אינכם יודעים כמה ממתקים יש בתוכו. הפעם, גם יש לכם 8 חברים. אם תוכלו לתת לכל אחד משמונת החברים שלכם בדיוק ממתק אחד, בלי שיישארו ממתקים בתיק, אז הקרדינליות של תיק הממתקים היא 8. אם לפחות חבר אחד לא קיבל ממתק, אז הקרדינליות של התיק קטנה מ־8. אם לפחות ממתק אחד נותר בתוך התיק, אז הקרדינליות של התיק גדולה מ־8.
קבוצה בַּת מְנִיָּה אינסופית
תארו לעצמכם עכשיו תיק המכיל את כל המספרים החיוביים: 1, 2, 3, 4 וכן הלאה. אנו משתמשים בסימן ℕ, כשהכוונה היא לתיק זה.2 מהי הקרדינליות של התיק ℕ? ודאי שהקרדינליות אינה ארבע, שֶׁכֵּן ℕ מכיל לפחות חמישה פריטים, כלומר: המספרים 1, 2, 3, 4 ו־5. אותו היגיון חל על כל מספר שהוא. אם תבחרו מספר כלשהו, למשל n, אז התיק ℕ יכיל לפחות n+1 פריטים, כלומר: המספרים 1, 2, 3, ..., n ו־n+1. מכאן, הקרדינליות של ℕ אינה מספר, ואנו אומרים כי ℕ הוא קבוצה בַּת מְנִיָּה אינסוֹפית.3
הגדרה: קבוצה בַּת מְנִיָּה אינסופית
תיק המכיל פריטים יהיה קבוצה בַּת מְנִיָּה אינסופית אם תהיה לו אותה קרדינליות כמו ℕ. במילים אחרות:
- התיק מכיל אינסוף פריטים, כך שנוכל להוציא ממנו משהו לָנֶצָח.
- נוכל לסדר בזוגות כל פריט שבתיק עם מספר שלם חיובי מסוים (זוהי דרך אחרת לומר שאפשר לספור את הפריטים).
דוגמה 1: מספרים זוגיים
תארו לעצמכם שני תיקים. אחד המכיל את כל המספרים החיוביים, שנקרא ℕ, ואחד המכיל את כל המספרים הזוגיים, שנקרא 2ℕ. טבעי יהיה לחשוב כי יש יותר מספרים חיוביים מאשר מספרים חיוביים זוגיים, אבל אנו נראה שאפשר לסדר בזוגות כל מספר זוגי עם מספר חיובי אחד מסוים, כך שבשני התיקים לא יישארו מספרים ללא בן זוג. הדבר יוכיח כי ל־ℕ ול־ℕ יש את אותה קרדינליות.
בטרם נעשה זאת, אנו זקוקים לדרך שתאפשר לנו להבחין בין המספרים שניקח מתיק ℕ ובין המספרים שניקח מתיק 2ℕ. הוספנו את הסימון “-י” לכל מספר שהוצאנו מתיק ℕ. דוגמאות:
- 6-י הוא מספר מ־ℕ ו־6 הוא מספר זוגי מ־2 ℕ.
- 7-י הוא מספר מ־ℕ, אבל היות שהמספר 7 אינו זוגי, הוא אינו מצוי בתיק 2ℕ.
הדרך ליצור זוגות בין מספרים מ־ℕ ומ־2ℕ היא לומר: המספר n-י נמצא בזוג עם המספר הזוגי 2n. למשל:
- המספר 4-י נמצא בזוג עם המספר הזוגי 8.
- המספר 5-י נמצא בזוג עם המספר הזוגי 10.
- המספר 57-י נמצא בזוג עם המספר הזוגי 114.
אנו רואים שֶׁכֹּל מספר מ־ℕ נמצא בזוג עם מספר זוגי. אנו גם רואים שֶׁכֹּל מספר זוגי נמצא בזוג עם מספר כלשהו, כי המספר הזוגי n נמצא בזוג עם המספר (n:2)-י. משמעות הדבר היא שהצלחנו לסדר בזוגות כל מספר מ־ℕ עם מספר מ־ 2 ℕ, ולא נותרו מספרים ללא בן זוג (איור 1). לפיכך, ל־ℕ ול־ 2 ℕ יש את אותה קרדינליות. תיק המספרים הזוגיים הוא קבוצה בַּת מְנִיָּה אינסופית. כלומר: מִנְיָן המספרים החיוביים זהה למִנְיָן המספרים החיוביים הזוגיים.
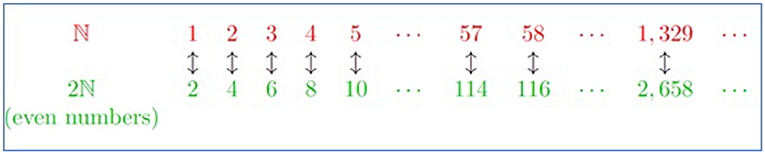
- איור 1 - כל מספר מ־ℕ נמצא בזוג עם מספר אחד מסוים מ־ℕ2.
- כך, מִנְיָן המספרים החיוביים זהה למִנְיָן המספרים החיוביים הזוגיים. Even numbers = מספרים זוגיים
חיבור אחת ועוד אינסוף
דוגמה 2: תארו לעצמכם שני תיקים, שבשניהם נמצאים כל המספרים החיוביים. כרגע, בשני התיקים יש את אותו מִנְיָן של פריטים (שניהם קבוצה בַּת מְנִיָּה אינסופית). עכשיו, הוסיפו פריט אחד, את האות A, לתיק השני. האם בתיק השני יש יותר פריטים מאשר בתיק הראשון? לא, למעשה יש בשניהם את אותו מִנְיָן פריטים. כמו קודם, נקרא לתיק הראשון ℕ, ונוסיף “-י” לסוף של כל מספר שנמצא בתיק. לתיק השני, המכיל A, 1, 2, 3 וכן הלאה, נקרא ℕ0. נסדר בזוגות כל פריט מתיק ℕ עם פריט יחיד מתיק ℕ0, תוך שימוש בשני חוקים:
- המספר 1-י יימצא בזוג עם האות A מ־ℕ0.
- כאשר n אינו 1, המספר n-י יימצא בזוג עם המספר n-1 מ־ℕ0.
דוגמאות:
- המספר 1-י יימצא בזוג עם האות A.
- המספר 5-י יימצא בזוג עם המספר 4.
- המספר 30-י יימצא בזוג עם המספר 29.
באופֶן זה, כל פריט מ־ℕ יימצא בזוג עם פריט יחיד מ־ℕ0. היות שכך, לשני תיקים יש את אותה קרדינליות, ואת אותו מִנְיָן פריטים.
היגיון זה פועל עבור כל מִנְיָן של דברים שנוסיף לתיק ℕ. לכן, לא משנה כמה פריטים סופיים נוסיף לתיק ℕ, התיק עדיין יהיה קבוצה בַּת מְנִיָּה אינסופית, ויכיל את אותו מִנְיָן פריטים.
חיבור אינסוף ועוד אינסוף
דוגמה 3: ראינו שתיק המכיל את כל המספרים החיוביים הוא קבוצה בַּת מְנִיָּה אינסופית. באותו היגיון, תיק המכיל את כל המספרים השליליים הוא קבוצה בַּת מְנִיָּה אינסופית. מה יקרה אם נשׂים בתיק אחד את כל המספרים החיוביים, את כל המספרים השליליים ואת הספרה ?0 האם תיק זה יהיה גדול יותר מתיק ℕ?
נשתמש בסימן ℤ עבור התיק המכיל את כל המספרים (חיוביים, שליליים ואפס).4 כדי ליצור זוגות בין המספרים מ־ℕ ומ־ℤ, עלינו להשתמש בחוקים מורכבים יותר.
- אם n הוא אי-זוגי, אז המספר n-י יימצא בזוג עם המספר (n-1):2 מ־ℤ.
- אם n הוא זוגי, אז המספר n-י יימצא בזוג עם המספר(n:2)-מ־ℤ.
דוגמאות:
- 4 הוא מספר זוגי, ו־4:2=2. לכן, המספר 4-י יימצא בזוג עם המספר 2-.
- 5 הוא מספר אי-זוגי, אז נחשב 5-1=4, ו־4:2=2. לכן, המספר 5-י יימצא בזוג עם המספר 2.
- המספר 24-י יימצא בזוג עם המספר 12-.
- המספר 57-י יימצא בזוג עם המספר 28.
שוב, סידרנו בזוגות כל פריט מ־ℕ עם פריט מ־ℤ (איור 2). כלומר, ℤ הוא קבוצה בַּת מְנִיָּה אינסופית. מִנְיָן המספרים (חיוביים ושליליים) זהה למִנְיָן המספרים החיוביים.

- איור 2 - כל מספר מ־ℕ יכול להימצא בזוג עם מספר יחיד מ־ℤ כך, מִנְיָן המספרים החיוביים זהה למִנְיָן המספרים החיוביים והשליליים.
- All numbers = כל המספרים
חיסור מאינסוף
ראינו שחיבור פריט אחד או אינסוף פריטים לתיק שהוא קבוצה בַּת מְנִיָּה אינסופית אינו גורם לתיק להיות גדול יותר (ראו דוגמה 3). אבל, מה יקרה אם נתחיל להוציא פריטים מתיק שהוא קבוצה בַּת מְנִיָּה אינסופית?
דוגמה 4: תארו לעצמכם את התיק המכיל את כל המספרים החיוביים, והוציאו ממנו את המספר 1. נקרא לתיק זה ℕ1. נראה שהתיק ℕ1 הוא קבוצה בַּת מְנִיָּה אינסופית, על-ידי יצירת זוגות בין כל פריט מ־ℕ1 עם פריט מ־ℕ. כמו קודם, נוסיף “-י” לסוף של כל מספר המגיע מ־ℕ. ניצור זוג של המספר n-י (מ־N) עם המספר n+1 (מ־ℕ1).
דוגמאות:
- המספר 1-י יימצא בזוג עם המספר 2.
- המספר 5-י יימצא בזוג עם המספר 6.
- המספר 30-י יימצא בזוג עם המספר 31.
כל פריט מ־ℕ יימצא בזוג עם פריט יחיד מ־ℕ1. מכאן, לשני התיקים יש את אותה קרדינליות, ואת אותו מִנְיָן פריטים. היגיון זה פועל עבור כל מִנְיָן של פריטים שנוציא מתיק ℕ. לא משנה כמה פריטים סופיים נוציא מ־ℕ, התיק עדיין יהיה קבוצה בַּת מְנִיָּה אינסופית, ועדיין יכיל את אותו מִנְיָן פריטים. עכשיו, מה יקרה אם מִנְיָן הפריטים שנוציא יהיה קבוצה בַּת מְנִיָּה אינסופית? במקרה זה, התשובה תלויה במה שנוציא.
דוגמה 5: אנו יודעים כי המספרים החיוביים הזוגיים הם קבוצה בַּת מְנִיָּה אינסופית (ראו דוגמה 1). תארו לעצמכם תיק המכיל את כל המספרים החיוביים, והוציאו מתיק זה את כל המספרים החיוביים הזוגיים. כל מה שיישאר בתיק הוא המספרים החיוביים האי-זוגיים. באותה דרך שבה המספרים הזוגיים הם קבוצה בַּת מְנִיָּה אינסופית, כך גם המספרים האי-זוגיים (כדי לראות זאת, ניצור זוגות של המספר n-י עם המספר האי-זוגי 2n-1, ראו איור 3).

- איור 3 - כל מספר מ־ℕ יכול להימצא בזוג עם מספר אי-זוגי יחיד.
- כך, מִנְיָן המספרים זהה למִנְיָן המספרים האי-זוגיים. Odd numbers = מספרים אי-זוגיים
במקרה זה, אם נתחיל בתיק שהוא קבוצה בַּת מְנִיָּה אינסופית ונוציא ממנו פריטים במִנְיָן קבוצה בַּת מְנִיָּה אינסופית, עדיין יישאר לנו מִנְיָן פריטים שהוא קבוצה בַּת מְנִיָּה אינסופית. במילים אחרות: נישאר עם תיק שהוא קבוצה בַּת מְנִיָּה אינסופית.
דוגמה 6: תארו לעצמכם תיק המכיל את כל המספרים החיוביים, כמו תיק ℕ. מתיק זה נוציא את כל המספרים הגדולים מ־1. מה שהוצאנו מהתיק ℕ הוא התיק ℕ1 (ראו דוגמה 4). אנו נישאר עם תיק המכיל את המספר 1. הקרדינליות של תיק המכיל רק את המספר 1 היא 1.
במקרה זה, התחלנו עם תיק שהוא קבוצה בַּת מְנִיָּה אינסופית, חיסרנו ממנו פריטים שמִנְיינם קבוצה בַּת מְנִיָּה אינסופית, ונותרנו עם פריט יחיד.
מסקנות
מאמר זה מראֶה כמה מההתנהגויות המוזרות של ה“אינסוף”. הדוגמאות האלה מראות כי אי אפשר לעסוק ב“אינסוף” כאילו היה מספר. כאשר אנו מְבַצְעִים פעולות חיבור או חיסור, ה“אינסוף” מתנהג אחרת ממספרים אחרים.
אומנם מוּזָרוּת זו בלבלה מתמטיקאים בהתחלה, אך כאשר חזרו ליסודות, הם הצליחו להבין את ה“אינסוף”. דבר זה חזר על עצמו לאורך ההיסטוריה – מושגים שפעם היו מסתוריים נהיו מובנים, כאשר נזהרו בהגדרתם.
מילון מונחים
קרדינליוּת (Cardinality): ↑ מִנְיָן הפריטים הנמצאים בתיק.
ℕ: ↑ “המספרים הטבעיים”, תיק המכיל את כל המספרים החיוביים: 1, 2, 3, 4, וכן הלאה.
קבוצה בַּת מְנִיָּה אינסוֹפית (Countably infinite): ↑ תיק המכיל אינסוף פריטים, אבל עדיין אנו יכולים לספור את הפריטים. במילים אחרות: תיק שהקרדינליות שלו זהָה לזו של תיק ℕ.
ℤ: ↑ המספרים "השלמים", תיק המכיל את כל המספרים השליליים, את כל המספרים החיוביים ואת הספרה אפס.
הצהרת ניגוד אינטרסים
המחברים מצהירים כי המחקר נערך בהעדר כל קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.
הערות שוליים
[1] ↑ במתמטיקה, אנו משתמשים במילה “קבוצה” כשאנו מתכוונים לתיק מלא פריטים.
[2] ↑ מדובר באות ℕ מודגשת. היא מסמלת “מספרים טבעיים” (natural numbers).
[3] ↑ אנו משתמשים במילים “בַּת מְניִהָּ” (countably) כי יש סוגים נוספים של אינסוף שהם גדולים יותר מבַתּ מְניִהָּ אינסופית לאין שיעור (אינפיניטסימלית).
[4] ↑ מדובר באות ℤ מודגשת. היא מסמלת את המילה הגרמנית ”“zahlen, שפירושה “מִסְפָּרִים”.
