ملخص
هل سبق لك أن كنت في فناء المدرسة تلعب لعبة تسمية أكبر عدد يمكن أن تفكر فيه؟ ما مدى سرعة قول أحدهم ”اللانهاية“؟ ثم يقول الشخص التالي: ”لانهاية زائد واحد“، وهكذا يبدو أن اللعبة لن تتوقف أبدًا. ولكن هل اللانهاية زائد واحد أكبر حقًا من اللانهاية؟ هل يمكننا إجراء العمليات الرياضية باستخدام اللانهاية؟ كان Georg Cantor (1845–1918) من أوائل علماء الرياضيات الذين درسوا اللانهاية، وتوصل إلى أمثلة مختلفة توضح اللانهاية في الرياضيات، كما اكتشف وجود أشكال مختلفة من اللانهاية، وأدى ذلك بدوره إلى رفض علماء الرياضيات الآخرين عمله باعتباره عملًا خاطئًا ومربكًا. كان David Hilbert هو من جعل اللانهاية قابلة للفهم من خلال مفارقة الفندق اللانهائي في عام 1924؛ يدور تفسيره حول قصة فندق كانت فيه غرفًا شاغرة جاهزة لاستقبال المزيد من النزلاء حتى عندما كان ممتلئًا، ونحاول في هذا المقال شرح اللانهاية بطريقة مماثلة.
مقدمة: الكاردينالية، التي تعني العد
اللانهاية هي شق غريب ومثير للجدل من عالم الرياضيات. حيث ندرك تلقائيًا وجود اللانهاية عندما نعرف لأول مرة أنه يمكننا الاستمرار في عد الأرقام إلى الأبد؛ ولمساعدتنا في فهم هذا السلوك الغريب، لجأ علماء الرياضيات إلى أساسيات علم الرياضيات وحاولوا تحديد معنى العد. تخيل أن لديك حقيبة مليئة بقطع الحلوى. ولا يمكنك رؤية ما بداخل الحقيبة، ولكنك تريد معرفة عدد قطع الحلوى التي لديك. أفضل طريقة لإجراء ذلك هي الوصول إلى ما بداخل الحقيبة، وإخراج قطعة الحلوى الأولى قائلًا: "واحد"، بعد ذلك، ستخرج قطعة الحلوى الثانية وتقول "اثنان"، وستستمر في فعل ذلك حتى تفرغ الحقيبة، وآخر رقم تقوله سيكون هو عدد قطع الحلوى التي لديك في حقيبتك. بهذه الطريقة نتعلم كيفية العد، مهما كانت العناصر الموجودة في حقيبتك.
تعريف: الكاردينالية
إن الكاردينالية (أو عدد الأصول) الخاصة بحقيبة مملؤة بعناصر1 هي عدد العناصر الموجودة داخل الحقيبة، ويمكن تحديد ذلك عن طريق إحصاء عدد العناصر الموجودة في الحقيبة.
على سبيل المثال، قيمة الكاردينالية لحقيبة بداخلها ثلاث قطع حلوى تساوي ثلاثة، كما تساوي قيمة الكاردينالية لحقيبة بداخلها قطعة حلوى واحدة وروبوت واحد وقلم رصاص واحد ثلاثة أيضًا. فليس من المهم طبيعة العناصر الموجودة بالحقيبة، ولكن ما يهمنا هو عددها، حيث يمكن أن تحتوي الحقيبة على عناصر أكثر تجريدًا؛ مثل حقيبة تحتوي على الأعداد 1 و2 و3.
فإذا كانت قيمة الكاردينالية أو عدد الأصول لحقيبتين مختلفتين متساوية، فستحتوي كلتا الحقيبتين على العدد نفسه من العناصر. ويمكننا أن نكون أزواجًا من العناصر في الحقيبتين دون أن يتبقى أي عنصر فردي في أي حقيبة منهما، ويقدم لنا ذلك طريقة أخرى لعد العناصر. إذا كنا نعرف قيمة الكاردينالية لإحدى الحقيبتين، ولا نعرف الأخرى، فيمكننا التحقق مما إذا كان بإمكاننا تكوين أزواج من العناصر في كلتا الحقيبتين أم لا.
فعلى سبيل المثال، لديك حقيبة من قطع الحلوى، ولكنك لا تعرف عدد القطع الموجودة بها، وهذه المرة، لديك أيضًا ثمانية أصدقاء. إذا كان بإمكانك أن تعطي قطعة حلوى واحدة لكل صديق من أصدقائك الثمانية، دون أن يتبقى أي قطع حلوى، فإن قيمة الكاردينالية لحقيبة الحلويات هي ثمانية، أما إذا لم يحصل صديق واحد على الأقل على قطعة حلوى، فإن قيمة الكاردينالية للحقيبة ستكون أقل من ثمانية، وإذا تبقت قطعة حلوى واحدة على الأقل، فستكون قيمة الأصلية أكثر من ثمانية.
قابلية العد إلى ما لانهاية
تخيل الآن حقيبة تحتوي على جميع الأعداد الموجبة: 1، و2، و3، و4، وما إلى ذلك، ونستخدم الرمز N للإشارة إلى هذه الحقيبة2 . ما قيمة الكاردينالية لهذه الحقيبة N؟ من الواضح أن قيمة الكاردينالية لها ليست 4، لأن N يحتوي على خمسة عناصر على الأقل، أي الأعداد 1، و2، و3، و4، و5، ويُطبق المنطق نفسه على أي رقم. اختر أي رقم، ليكن مثلًا n، وبالتالي سيحتوي الرمز N للحقيبة على الأقل على n + 1 من العناصر، أي الأعداد 1، و2، و3، ...، و"n"، وn + 1. يوضح هذا أن قيمة الكاردينالية ل−N ليست رقمًا، ونقول إن N هي مجموعة قابلة للعد إلى ما لانهاية3.
تعريف: مجموعة قابلة للعد إلى ما لانهاية.
تعتبر حقيبة مملؤة بالعناصر قابلة للعد إلى ما لانهاية إذا كانت قيمة الكاردينالية لها تساوي قيمة الحقيبة N. وبعبارة أخرى:
(1) تحتوي الحقيبة على عدد لا نهائي من العناصر، بحيث نستطيع أخذ عناصر منها إلى الأبد دون توقف.
(2) يمكننا إقران كل عنصر في الحقيبة بعدد صحيح موجب مميز (وهي طريقة أخرى لقول إنه يمكننا حساب عدد العناصر).
مثال 1: الأعداد الزوجية
تخيل أن هناك حقيبتين؛ إحداهما تحتوي على جميع الأعداد الموجبة، وتُسمى N، والأخرى تحتوي على الأعداد الموجبة الزوجية جميعها، وتُسمى 2N، وقد يبدو من الطبيعي أن نعتقد أن هناك أعدادًا موجبة أكثر من الأعداد الموجبة الزوجية، ولكننا سنوضح أنه يمكنك إقران كل عدد زوجي برقم واحد بالضبط، بحيث لا يكون هناك أي أعداد متبقية مما سيوضح أن N و2N لهما قيمة الكاردينالية نفسها.
قبل إجراء ذلك، نحن بحاجة إلى طريقة للتمييز بين الأعداد التي نختارها من الحقيبة N، والأعداد التي نختارها من الحقيبة 2N، وعليه سنضيف "th" في نهاية العدد الذي نختاره من الحقيبة N، على سبيل المثال:
- 6th هو عدد من الحقيبة N و6 هو عدد زوجي من الحقيبة 2N،
- 7th هو رقم من الحقيبة N، ولكن 7 ليس عددًا زوجيًا، فهو غير موجود في الحقيبة 2N،
وتكون طريقة إقران الأعداد من الحقيبة N والحقيبة 2N هي قول: إن العدد nth مقترن بالعدد الزوجي 2n.
أمثلة على ذلك:
- العدد 4th مقترن بالعدد الزوجي 8.
- العدد 5th مقترن بالعدد الزوجي 10.
- العدد 57th مقترن بالعدد الزوجي 114.
نلاحظ أن كل عدد من الحقيبة N مقترن بعدد زوجي، كما نرى أيضًا أن كل عدد زوجي مقترن بعدد، حيث يقترن العدد الزوجي n بالعدد (n ÷ 2)th، وهذا يعني أننا أجرينا عملية إقران لكل عدد في الحقيبة N مع عدد في الحقيبة 2N، ولا توجد أي أعداد متبقية (الشكل 1). وبالتالي، N و2N لهما قيمة الكاردينالية نفسها، وتكون حقيبة الأعداد الزوجية هي المجموعة القابلة للعد إلى ما لانهاية، هذا يعني أن هناك المقدار نفسه من الأعداد الموجبة كما هو الحال مع الأعداد الموجبة الزوجية.
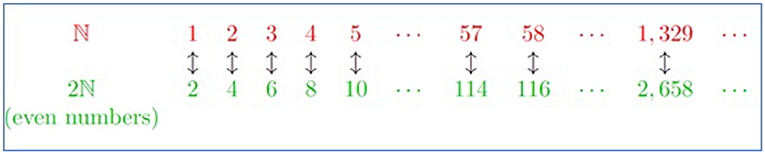
- شكل 1 - يمكن إقران كل عدد من الحقيبة N مع عدد زوجي واحد من الحقيبة 2N، لذا يوجد الكثير من الأعداد مثلما توجد أعداد زوجية كثيرة.
إضافة عنصر واحد إلى اللانهاية
مثال 2: تخيل أن هناك حقيبتين، تحتوي كلتاهما على جميع الأعداد الموجبة؛ تحتوي كلتا الحقيبتين حاليًا على العدد نفسه من العناصر (كلتاهما مجموعتان قابلتان للعد إلى ما لانهاية). أضف الآن عنصرًا واحدًا، هو الحرف أ، إلى الحقيبة الثانية. هل تحتوي الحقيبة الثانية على عناصر أكثر من الحقيبة الأولى؟ لا، ففي الواقع سيكون بهما العدد نفسه من العناصر، كما كان الحال من قبل، نطلق على الحقيبة الأولي اسم N، وسنضيف "th" في نهاية كل عدد من هذه الحقيبة. أما الحقيبة الثانية، التي تحتوي على أ، و1، و2، و3، وما إلى ذلك فسنطلق عليها اسم N0، وسنقرن كل عنصر في الحقيبة N مع عنصر واحد من الحقيبة N0 باستخدام قاعدتين:
(1) العدد 1th مقترن بالحرف أ من الحقيبة N0.
(2) عندما لا يكون n واحدًا، يقترن العدد nth مع العدد n – 1 من الحقيبة N0.
على سبيل المثال
- العدد 1th مقترن بالحرف أ.
- العدد 5th مقترن بالعدد 4.
- العدد 30th مقترن بالعدد 29.
بهذه الطريقة، يقترن كل عنصر في الحقيبة N مع عنصر واحد في الحقيبة N0، ولذلك، فإن كلتا الحقيبتين لهما قيمة الكاردينالية نفسها، وبالتالي العدد نفسه من العناصر، ويسري هذا المنطق على أي أعداد من العناصر التي نضيفها إلى الحقيبة N. لذلك، بغض النظر عن عدد العناصر المتناهية التي نضيفها إلى الحقيبة N، ما تزال الحقيبة تمثل مجموعة قابلة للعد إلى ما لانهاية وتحتوي على العدد نفسه من العناصر.
إضافة عدد لانهائي إلى اللانهاية
مثال 3: لقد لاحظنا كيف أن الحقيبة التي تحتوي على جميع الأعداد الموجبة هي مجموعة قابلة للعد إلى ما لانهاية، وبالمنطق ذاته، فإن الحقيبة التي تحتوي على جميع الأعداد السالبة هي مجموعة قابلة للعد إلى ما لانهاية أيضًا. ماذا سيحدث لو وضعنا، في حقيبة واحدة، جميع الأعداد الموجبة وجميع الأعداد السالبة والعدد 0؟ هل ستكون هذه الحقيبة أكبر من الحقيبة N؟
سنستخدم الرمز Z للإشارة إلى الحقيبة التي تحتوي على جميع الأعداد (الموجبة والسالبة والصفر)4. ولإقران الأعداد في الحقيبة N مع الأعداد في الحقيبة Z، علينا استخدام قواعد أكثر تعقيدًا.
(1) عندما يكون n عددًا فرديًا، يقترن العدد nth مع العدد (n − 1)
÷ 2 في الحقيبة Z.
(2) عندما يكون n عددًا زوجيًا، يقترن العدد nth مع العدد−(n ÷ 2) في الحقيبة Z.
على سبيل المثال:
- 4 عدد زوجي و 4 ÷ 2 = 2. لذلك، يقترن العدد 4th بالعدد −2.
- 5 عدد فردي، لذا نقول إن 5 − 1 = 4 و4 ÷ 2 = 2. لذلك، يقترن العدد 5th بالعدد 2.
- يقترن العدد 24th بالعدد −12.
- يقترن العدد 57th بالعدد 28.
لقد أجرينا مرة أخرى عملية اقتران بين كل عنصر في الحقيبة N مع عنصر في الحقيبة Z (الشكل 2)، وهذا يعني أن للحقيبتين قيمة الكاردينالية نفسها، وبالتالي، الحقيبة Z هي مجموعة قابلة للعد إلى ما لانهاية، ويوجد الكثير من الأعداد (الموجبة والسالبة) مثلما يوجد الكثير من الأعداد الموجبة.

- شكل 2 - يمكن إقران كل عدد من الحقيبة N مع عدد واحد من الحقيبة Z، لذا سيوجد الكثير من الأعداد مثلما يوجد الكثير من الأعداد الموجبة والسالبة.
الطرح من اللانهاية
لقد لاحظنا كيف أن إضافة عنصر أو عدد لا نهائي من العناصر إلى حقيبة المجموعة القابلة للعد إلى ما لانهاية لا يجعل الحقيبة أكبر (انظر المثال 3)، ولكن، ماذا يحدث إذا بدأنا في إزالة العناصر من حقيبة المجموعة القابلة للعد إلى ما لانهاية؟

- شكل 3 - يمكن إقران كل عدد من الحقيبة N مع عدد فردي واحد، لذا يوجد الكثير من الأعداد مثلما توجد أعداد فردية كثيرة.
مثال 4: تخيّل أن هناك حقيبة تحتوي على جميع الأعداد الموجبة ونقوم بإزالة الرقم 1 منها، وسنطلق على هذه الحقيبة اسم N1؛ يتبين لنا أن الحقيبة N1 هي مجموعة قابلة للعد إلى ما لانهاية من خلال إقران كل عنصر من الحقيبة N1 مع عنصر من الحقيبة N. كما فعلنا من قبل، سنضيف "th" إلى نهاية كل عدد من الحقيبة N. سنقرن الرقم n (من N) مع الرقم n + 1 من الحقيبة N1.
أمثلة
- العدد 1th مقترن بالعدد 2.
- العدد 5th مقترن بالعدد 6.
- العدد 30th مقترن بالعدد 31.
يقترن كل عنصر في الحقيبة N مع عنصر واحد في الحقيبة N1، ولذلك، فإن كلتا الحقيبتين لهما قيمة الكاردينالية نفسها، وبالتالي العدد نفسه من العناصر.
ويسري هذا المنطق على أي أعداد من العناصر التي نطرحها من الحقيبة N. لذلك، بغض النظر عن عدد العناصر المتناهية التي نُزيلها من الحقيبة N، ما تزال الحقيبة تعتبر مجموعة قابلة للعد إلى ما لانهاية، وما تزال تحتوي على العدد نفسه من العناصر.
الآن، ماذا لو أزلنا العديد من العناصر القابلة للعد إلى ما لانهاية؟ حينها ستعتمد الإجابة على العناصر التي سنزيلها.
مثال 5: نعلم أن الأعداد الزوجية الموجبة هي مجموعة قابلة للعد إلى ما لانهاية (انظر المثال 1). تخيل أن هناك حقيبة تحتوي على جميع الأعداد الموجبة، وسنقوم بإزالة جميع الأعداد الزوجية الموجبة من تلك الحقيبة، بحيث يكون كل ما تبقى في الحقيبة هو الأعداد الفردية الموجبة؛ وبنفس الطريقة التي تكون فيها الأعداد الزوجية مجموعة قابلة للعد إلى ما لانهاية، فإن الأعداد الفردية تكون مجموعة معدودة لانهائية أيضًا (لمعرفة ذلك، نقرن الرقم nth مع الرقم الفردي 2n, − 1، انظر الشكل 3).
في هذه الحالة، نكون قد بدأنا بحقيبة بها مجموعة معدودة لانهائية ثم قمنا بإزالة عناصر مجموعة معدودة لانهائية منها، وما زال يتبقى أمامنا الكثير من العناصر المعدودة اللانهائية، أو بعبارة أخرى، يتبقى لدينا حقيبة بها مجموعة معدودة لانهائية.
مثال 6: تخيل أن هناك حقيبة تحتوي على جميع الأعداد الموجبة، مثل الحقيبة N ولتتخيل أننا أزلنا جميع الأعداد الأكبر من 1. ستجد أن ما أزلناه من الحقيبة N هو الحقيبة N1 (انظر المثال 4)، وما تبقى لدينا هو حقيبة تحتوي على الرقم 1، ويكون للحقيبة التي تحتوي على الرقم 1 قيمة كاردينالية تساوي 1.
في هذه الحالة، نكون قد بدأنا بحقيبة بها مجموعة معدودة لانهائية، ومع إزالة عناصر مجموعة معدودة لانهائية منها، يتبقى لدينا عنصر واحد.
الخلاصة
يوضح هذا المقال بعض السلوكيات الغريبة للانهاية، حيث توضح الأمثلة أعلاه أنه لا يمكن التعامل مع اللانهاية باعتبارها عددًا، فعندما نُجري عمليتي الجمع والطرح، تسلك اللانهاية سلوكًا مختلفًا عن الأعداد.
وفي حين أن هذا السلوك الغريب أربك علماء الرياضيات في البداية، إلا أنهم تمكنوا من فهم اللانهاية من خلال العودة إلى الأساسيات، وقد ثبت مرارًا وتكرارًا على مر التاريخ أن المفاهيم التي كانت غامضة ذات يوم أصبحت مفهومة أخيرًا من خلال الحرص على وضع تعريف لها، وتوصيفها.
مسرد للمصطلحات
الكاردينالية (عدد الأصول) (Cardinality): ↑ هي عدد العناصر الموجودة في حقيبة.
المجموعة N: ↑ تمثل "الأعداد الطبيعية"، أي الحقيبة التي تحتوي على كل الأعداد الموجبة 1، و2، و3، و4، وما إلى ذلك.
مجموعة قابلة للعد إلى ما لانهاية: ↑ حقيبة تحتوي على عدد لا نهائي من العناصر، ولكن ما يزال بإمكاننا عد العناصر. أو بعبارة أخرى، حقيبة لها نفس قيمة الكاردينالية للمجموعة N.
المجموعة Z: ↑ هي مجموعة ”الأعداد الصحيحة”، أي الحقيبة التي تحتوي على جميع الأعداد السالبة، والعدد صفر وجميع الأعداد الموجبة.
إقرار تضارب المصالح
يعلن المؤلفون أن البحث قد أُجري في غياب أي علاقات تجارية أو مالية يمكن تفسيرها على أنها تضارب محتمل في المصالح.
الحواشي
1 ↑ في الرياضيات، نستخدم كلمة "مجموعة" للإشارة إلى حقيبة من العناصر.
2 ↑ والرمز N بهذا الخط العريض، يرمز إلى "الأعداد الطبيعية".
3 ↑ ونستخدم الصفة "قابلية العد"، حيث توجد أشكال أخرى من ال ا لنهاية أكبر من ال ا لنهاية القابلة للعد.
4 ↑ الرمز Z بهذا الخط العريض، يرمز إلى ،"zahlen" وتعني "الأعداد" باللغة الألمانية.
