תַקצִיר
חשיבה מרחבית מאפשרת לכם להבין את המיקום של אובייקטים, את הממדים שלהם ואת האופן שבו אובייקטים שונים קשורים זה לזה. היא גם מאפשרת לכם לדמוֹת ולשחק עם אובייקטים וצורות בדמיון שלכם. חשיבה מרחבית חשובה מאוד לא רק עבור מטלות יומיומיות, אלא שמחקר חדש מראה שהיא הכרחית ללמידת מתמטיקה. ילדים ובני נוער שטובים במטלות מרחביות גם טובים בשאלות מתמטיות. החדשות הטובות הן שהרבה מחקרים הראו שאתם יכולים לשפר את החשיבה המרחבית שלכם על ידי ''אימון''. משמעות הדבר היא שתרגול משחקים מרחביים וביצוע פעילויות מרחביות יכול לשפר את הביצועים המרחביים שלכם. במאמר זה נדון בדרכים שבהן אתם יכולים לשפר את החשיבה המרחבית שלכם, ונסתכל על רְאָיוֹת שמציעות כי אימון מרחבי עשוי גם לשפר ביצועים במתמטיקה.
הקדמה
כיצד אתם יודעים איך לארגן אובייקטים כמו למשל לארוז מזוודה או להכניס את הספר שלכם לילקוט? כיצד אתם יודעים איך לנעול נעליים על הרגל הנכונה, וכיצד לכפתר את החולצה שלכם בצורה הנכונה? כיצד אתם מוצאים את דרככם במרכז קניות, וכיצד אתם יודעים מה לעשות אם אתם יורדים בתחנת האוטובוס הלא נכונה? המטלות האלה נסמכות על יכולות מרחביות. אנשים תלויים ביכולות החשיבה המרחבית שלהם מאות פעמים ביום בלי להבחין בכך. אפילו מעבר לפעילויות יומיומיות, מרבית האנשים, כולל מורים, לא מבינים שחשיבה מרחבית יכולה להשפיע על ההצלחה בבית הספר במיוחד בשיעורי מתמטיקה. אם כן, מהי חשיבה מרחבית, והאם ניתן להפוך למומחה בחשיבה מרחבית?
חשיבה מרחבית – כיצד מודדים אותה?
אנו משתמשים בחשיבה מרחבית כדי להבין את המיקום של אובייקטים ואת הממדים שלהם (כמו למשל אורך וגודל), וכיצד אובייקטים שונים קשורים זה לזה. חשוב להבין שחשיבה מרחבית היא לא רק כישור אחד, אלא סֶט של כישורים שונים. חלק מהכישורים המרחביים החשובים ביותר והמבחנים שמדענים עושים במטרה למדוד אותם, מתוארים למטה.
סיבוב מנטלי
סיבוב מנטלי מאפשר לנו להפוך (לעשות מניפולציה על) תמונות בדמיון שלנו. אתם יכולים לנסות לעצום את עיניכם ולדמיין אובייקט כמו מכונית. כעת, האם אתם יכולים לדמיין כיצד המכונית הייתה נראית אם היא הייתה מתהפכת מלמעלה למטה? כדי לעשות זאת, אתם צריכים להשתמש בסיבוב מנטלי. באיור 1, אתם יכולים לראות מבחן לסיבוב מנטלי. האם אתם יכולים לבחור איזו תמונה בחלק התחתון זהה לתמונה שלמעלה? כדי לפענח את זה, אתם צריכים להפוך את הפרות בדמיונכם. אז, אתם יכולים לומר שהפרה משמאל היא אותו הדבר כמו הפרה שלמעלה.

- איור 1 - דוגמה למטלת סיבוב מנטלי.
לא משנה כמה אתם מסובבים את הפרה שמימין, היא תמיד תפנה לכיוון הלא נכון. השלמת המבחן הזה דורשת סיבוב מנטלי. אפשר לא רק להפוך אובייקטים בדמיון, אלא גם לדמיין כיצד אובייקט היה נראה אם הוא היה שבור לחצי, מקופל, או מכופף.
הפרדת אובייקט מרקע מורכב (Disembedding)
כישורים שנקראים disembedding מתייחסים לכישורים המרחביים שנדרשים כדי להפריד אובייקט אחד או תמונה מרקע מורכב. זה מאפשר לנו להבין כיצד מבנים מורכבים בנויים מחלקים נפרדים. דוגמה פשוטה מאוד לכך מוצגת באיור 2. האם אתם יכולים למצוא את הצורה הכתומה בתמונה המורכבת יותר?
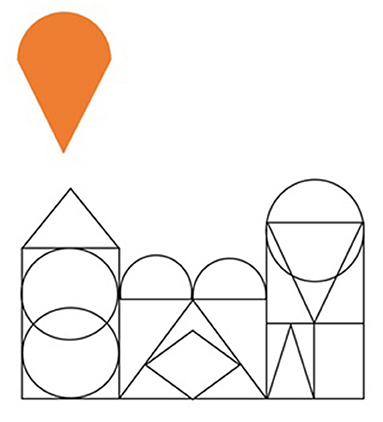
- איור 2 - דוגמה למטלת .disembedding
המרת קנה מידה מרחבי (Spatial Scailing)
המרת קנה מידה מרחבי היא היכולת להמיר מידע בין ייצוגים בגדלים שונים. לדוגמה, המרת קנה מידה מרחבי נדרשת כדי להבין שהתמונה של פארק שאתם רואים על המפה בטלפון הנייד שלכם מייצגת את אותו הפארק שאתם עומדים בו. דוגמה אחרת היא כאשר אנו מרכיבים רהיטים כמו שידת מגירות באמצעות הוראות נייר עם דיאגרמות קטנות. כדי לבנות שידת מגירות אתם צריכים להיות מסוגלים להבין שהתמונה הקטנה של דלת השידה בדיאגרמה מייצגת את הדלת בגודל האמיתי שאתם צריכים להרכיב. בכל תמונה באיור 3 ישנו כדור שממוקם בין שני עצים. איזו תמונה מבין השתיים התחתונות זהה לתמונה שלמעלה? תבחינו בכך ששתי התמונות התחתונות אינן זהות בגודלן לתמונה שלמעלה. משמעות הדבר היא שאתם צריכים להשתמש בהַתְמָרַת קנה מידה מרחבי כשאתם משווים אותן (התשובה הנכונה היא התמונה שמשמאל).
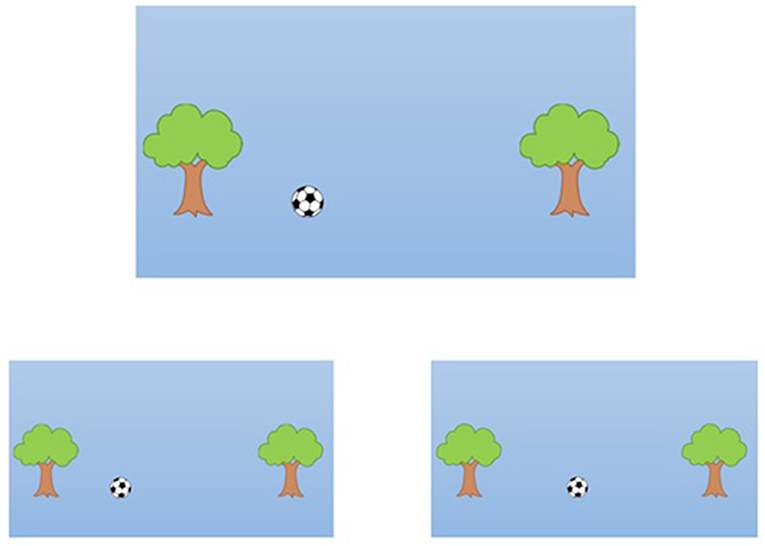
- איור 3 - דוגמה למטלה של התמרת קנה מידה מרחבי.
ניווט
כישורי ניווט הכרחיים לתנועה בסביבה שלנו ולהגעה למקומות שאנו צריכים להגיע אליהם. כדי לנווט כראוי אתם צריכים להיות מסוגלים להבין את הקשרים שבין בניינים, להשתמש בסימני דרך, לדמיין איך רחובות או בניינים יֵרָאוּ מפרספקטיבות שונות, ללמוד את הדרכים ולבסס הבנה של פרישׂת הסביבה שלכם.
חשיבה מרחבית חשובה בבית הספר ובעבודה
מעבר לחשיבות הברורה בחיי היומיום, מתברר שחשיבה מרחבית חשובה גם להצלחה שלנו בבית הספר, ובפרט בשיעורי המתמטיקה. אנשים שטובים במטלות חשיבה מרחבית גם מקבלים ציונים טובים במבחנים במתמטיקה. הקשר שבין חשיבה מרחבית טובה לבין ביצועים מתמטיים טובים קיים אצל אנשים בגילים שונים. לדוגמה, מחקר הראה כי פעוטות שטובים יותר בבניית אבני בניין מצליחים יותר במבחני ספירה ומספרים [1]. עבור ילדים בבית ספר יסודי, הרבה חוקרים הראו כי סוגים שונים של חשיבה מרחבית חשובים עבור מטלות מתמטיות שונות [2]. ילדים שטובים בהמרת קנה מידה מרחבי גם טובים במיקום מספרים על ציר המספרים, וילדים שטובים בסיבוב מנטלי גם טובים בביצוע מטלות חישוב עם מספרים חסרים, כמו: 3 + □ = 5. עבור מבוגרים, כישורים מרחביים טובים חשובים מאוד לעבודות מסוימות. לדוגמה, מהנדסים זקוקים לכישורים מרחביים כדי לדמיין את המבנה של גשר או בניין; גיאולוגים זקוקים לכישורים מרחביים כך שיוכלו לנווט בטבע; רופאים צריכים כישורים מרחביים כדי לוודא שהם נותנים זריקות במקום הנכון וכדי לקרוא צילומי רנטגן כראוי, וביולוגים זקוקים לכישורים מרחביים כדי להבין כיצד מזון נע דרך חלקים שונים במערכת העיכול שלנו. מחקרים מראים כי אנשים שיש להם כישורים מרחביים טובים הם בני נוער שבדרך כלל ממשיכים למקצועות של מדע, טכנולוגיה, הנדסה ומתמטיקה בחייהם הבוגרים.
מה אם איני טוב/ה במטלות מרחביות?
החדשות הטובות הן שאם אינכם טובים במיוחד בפעילויות מרחביות, אינכם צריכים לדאוג. חשיבה מרחבית היא כישור קוגניטיבי שנראה כמגיב די טוב לאימון. הרבה מחקרים ניסו לשפר את היכולת המרחבית דרך סוגים שונים של אימון קוגניטיבי. אף על פי שהמילה ''אימון'' לעיתים קרובות מקושרת עם אימון גופני, כאשר מדענים קוגניטיביים (ומדעני מוח) משתמשים במילה זו, הם בדרך כלל מתכוונים לתרגול. משמעות הדבר היא ש''אימון מרחבי'' בדרך כלל מְעָרֵב תרגול מטלות מרחביות עם נייר ועפרון, השלמת משחקים מרחביים במחשב, או ביצוע פעילויות מרחביות כמו בניית מבנים עם לבנים. מחקרים רבים הראו שאם אתם מתאמנים, החשיבה המרחבית שלכם יכולה להשתפר [3].
חדשות טובות אפילו יותר מגיעות ממחקר חדש שמראה כי אם אתם משפרים את החשיבה המרחבית שלכם, אתם גם משתפרים במבחנים במתמטיקה. כאשר אימון בכישור אחד מוביל לשיפור בכישור אחר, זה נקרא העברה .(transfer) מחקרים על סוגים אחרים של חשיבה מראים שקשה לגרום לאימון מוחי לעבור לכישורים שאינם מאומנים. אתם יכולים לקרוא כאןe על סוגים אחרים של אימון מוחי, ואם הם פועלים [7]. לכן, אימון מרחבי הוא די ייחודי וחשוב מאחר שישנן ראיות לכך שאימון חשיבה מרחבית אכן מועבר לכישורים אחרים, לדוגמה למתמטיקה.
מחקר עכשווי שהשלמתי הראה כי ילדים קיבלו ציונים גבוהים יותר במבחן במתמטיקה אחרי שהם צפו בווידיאו קצר על חשיבה מרחבית [4]. חוקרים אחרים הראו גם ששימוש בטַנְגְרָמִים, שהם סוג של פאזל, ובמשחקים מרחביים אחרים יכול לשפר את כישורי המתמטיקה [5]. לרוע המזל, חשיבה מרחבית אינה נלמדת לרוב בבית ספר. אולם ישנן דרכים שבהן אתם יכולים להכניס אותה לחייכם בקלות, בבית ובבית הספר. זה כולל שימוש בדיאגרמות ובגרפים נוספים שיסייעו לכם כשאתם לומדים נושאים חדשים בבית הספר; שימוש בשפה מרחבית יותר כולל מילים כמו למעלה, מעבר, מסביב, דרך, במקביל, סימטרי וביצוע מחוות כשאתם מסבירים נושאים מורכבים לחברים או לאחים הצעירים שלכם; אימון בבניית דברים עם לבנים, לגו, או פאזלים, הרכבת רהיטים או אפילו עטיפת מתנות. ייתכן גם שחלק ממשחקי המחשב כמו ''שוֹלה המוקשים'' (שבו שחקנים צריכים להשתמש בלבנים תלת-ממדיות כדי לבנות מבנים כמו בתים וערים), או משחקים שדורשים משחקנים לנווט במבוכים או במקומות בלתי מוכרים, עשויים לשפר חשיבה מרחבית.
מדוע חשיבה מרחבית חשובה למתמטיקה?
כחוקרים, אחת השאלות שאנו עדיין מנסים לענות עליה היא מדוע כישורים מרחביים ומתמטיים מקושרים זה לזה. במילים אחרות, מדוע אנשים שטובים בחשיבה מרחבית טובים גם במתמטיקה? אפשרות אחת היא שאותם אזורים במוח שאנו משתמשים בהם עבור מטלות מרחביות משמשים גם עבור מתמטיקה. דרך אחת לראות אלו חלקים במוח מופעלים כאשר אנו עושים סוגים מסוימים של פעילויות היא דרך דימוּת תהודה מגנטית תפקודי (fMRI). השיטה הזו משתמשת בסורק שמראה אלו אזורים במוח פעילים בזמנים שונים. לדוגמה, היא יכולה לשמש לומר איזה אזור במוחכם נעשה פעיל כשאתם עושים פעילות מתמטית. מחקרים מראים שכישורים מרחביים ומתמטיים מסוימים נסמכים על אותו אזור במוח, שנקרא האונה הקודקודית [6]. משמעות הדבר היא שתוכניות אימון אשר מעודדות אותנו להשתמש בחשיבה מרחבית עשויות לחזק את הקשרים בין תאי עָצָב (נוירונים) באזור הזה במוח. הדבר שימושי הן עבור חשיבה מרחבית הן עבור מתמטיקה.
מסקנות
בפעם הבאה שאתם מנסים לדחוס כמה שיותר בגדים לתוך המזוודה שלכם, או שאתם עוקבים בזהירות אחרי המפה בטלפון הנייד שלכם, זכרו כמה הכישורים המרחביים שלכם יקרי ערך. ייתכן אפילו שיותר מכישורי אוריינות ומחשיבה כמותית, לכישורי חשיבה מרחבית יש השפעה ענקית על האופן שבו אנו מתנהלים ומתפקדים בחיי היומיום שלנו. נוסף על כך כפי שתואר במאמר הזה, שימוש בהזדמנויות נוספות כדי לתרגל את כישורי החשיבה המרחבית שלנו עשוי גם לשפר את כישורי המתמטיקה שלנו. בואו ניצור מקום לפיתוח החשיבה המרחבית שלנו!
מילון מונחים
חשיבה מרחבית (Spatial Thinking): ↑ האופן שבו המוח מעבד את המיקום של צורה או של אובייקטים שונים.
מתמטיקה (Mathematics): ↑ מקצוע שקשור למספרים ולכמויות.
אימון קוגניטיבי (Cognitive Training): ↑ אימון או תרגול של כישורי חשיבה מסוימים, בכוונה לשפּרם.
הצהרת ניגוד אינטרסים
המחבר מצהיר על הכל המחקר נערך בהעדר כי קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.
תודות
אנו רוצים להודות מקרב לב לאלה שסייעו בתרגום המאמרים באוסף הזה במטרה לעשותם נגישׁים יותר עבור ילדים מחוץ למדינות דוברות אנגלית, ולקרן Jacobs עבור סיפוק הכספים הנדרשים לתרגום המאמרים. בהקשר מאמר זה, אנו רוצים להודות במיוחד לניינק ואן-אטבלדא ולסאבין פיטרס עבור התרגום להולנדית.
מאמר המקור
↑ Gilligan, K. A., Hodgkiss, A., Thomas, M. S., and Farran, E. K. 2019. The developmental relations between spatial cognition and mathematics in primary school children. Dev. Sci. 22:e12786. doi: 10.1111/desc.12786
מקורות
[1] ↑ Verdine, B. N., Golinkoff, R. M., Hirsh-Pasek, K., Newcombe, N. S., Filipowicz, A. T., and Chang, A. 2014. Deconstructing building blocks: preschoolers’ spatial assembly performance relates to early mathematical skills. Child Dev. 85:1062–76. doi: 10.1111/cdev.12165
[2] ↑ Mix, K. S., Levine, S. C., Cheng, Y.-L., Young, C., Hambrick, D. Z., Ping, R., et al. 2016. Separate but correlated: the latent structure of space and mathematics across development. J. Exp. Psychol. Gen. 145:1206–27. doi: 10.1037/xge0000182
[3] ↑ Uttal, D. H., Meadow, N. G., Tipton, E., Hand, L. L., Alden, A. R., Warren, C., et al. 2013. The malleability of spatial skills: a meta-analysis of training studies. Psychol. Bull. 139:352–402. doi: 10.1037/a0028446
[4] ↑ Gilligan, K. A., Thomas, M. S. C., and Farran, E. K. 2019. First demonstration of effective spatial training for near-transfer to spatial performance and far-transfer to a range of mathematics skills at 8 years. Dev. Sci. e12909. doi: 10.1111/desc.12909
[5] ↑ Cheng, Y. L., and Mix, K. S. 2014. Spatial training improves children’s mathematics ability. J. Cogn. Dev. 15:2–11. doi: 10.1080/15248372.2012.725186
[6] ↑ Hawes, Z., Moriah Sokolowski, H., Ononye, C. B., and Ansari, D. 2019. Neural underpinnings of numerical and spatial cognition: An fMRI meta-analysis of brain regions associated with symbolic number, arithmetic, and mental rotation. Neurosci. Biobehav. Rev. 103:316–33. doi: 10.1016/j.neubiorev.2019.05.007
[7] ↑ Goffin, C., and Ansari, D. 2018. Can brain training train your brain? Using the scientific method to get the answer. Front. Young Minds 6:26. doi: 10.3389/frym.2018.00026
