Abstract
When designing schools and highways, engineers need to know how people might move through these structures. If they can accurately describe how crowds will react to their designs before they build the various structures, they can prepare for emergencies, avoid traffic jams, and make the flow of crowds more efficient. In this article, we provide an introduction to the mathematical modeling of traffic flow by describing how individual people might act while moving in large crowds. We provide links to an experiment with real people, a model of the experiment, and interactive simulations for readers to see how well the mathematical model mimics a real crowd and for the readers to explore the features of similar models.
Why Do We Study Crowds?
Have you ever tried walking through a super busy school hallway? It can be pretty tricky with everyone going different ways. How do you navigate through the crowd without bumping into everyone? You have probably noticed it is a lot easier to move when people are going in the same direction as you.
Scientists and engineers are interested in figuring out how people move in places with lots of people, like roads, airports, schools, and theme parks. Why? Because it is super important to make sure everyone stays safe. Think about it: when you are in a big building, like a school or a mall, and there is an emergency, you need to know the best way to get out fast. Scientists help decide how many emergency exits are needed and where to put them by understanding how people move and react in big crowds.
Of course, it is really helpful for engineers to know how people would move in a building before they build it. That way, they can design the building to be as safe as possible. The study of how people move is usually called the study of crowd dynamics, and by using mathematical models, engineers can discover surprising behavior about evacuation scenarios before they happen [1, 2]. But how can scientists and engineers model how people move in crowded places? In this article, we will talk about a particular way that mathematicians model crowds to answer this question.
An Experiment: A Crowded Hallway
Let us start by watching an experiment of people walking through a crowded hallway in this Physics World video. In the video, those in red shirts are walking to the left, and those in blue shirts are going to the right. When a bunch of people are moving in opposite directions like this, it is called counter flow. Counter flow is a good starting point when studying crowd dynamics, because it is not too complicated and not too boring [3–5].
In the video, did you see what happened when the hallway got really crowded? The people in red stuck together, and the folks in blue formed their own group. They created lanes, just like those going in different directions on a road. This seems like a good strategy! Imagine you are in a big crowd, and you want to go in a certain direction. If you join up with others who are heading the same way, it is like forming a team. This makes it much easier to move around and get to where you want to go. Teamwork helps us navigate through busy places. But is this something that people choose to do, or do these lanes form naturally?
Interacting Particle Systems
So, how can we model and simulate this behavior? Mathematicians use a tool called interacting particle systems (IPSs). The main idea behind IPSs is that they can describe what a single particle does and how it interacts with others and, by simulating many particles, build up the crowd from there. For instance, in Figure 1 we have a blue particle, named Blake, that wants to move to the right.

- Figure 1 - A particle (which we will call Blake) with a circular interaction region and movement in a certain direction, represented by an arrow.
Blake has a circle around it. We call this area the interaction region, and it is kind of like Blake’s personal bubble! When someone else enters the bubble, Blake will react; just like you would react if someone stood too close. This region also does not have to be a circle. There are many different shapes which could make sense in different situations. In Figure 2, you can see some other common types of interaction regions. But for now, we will stick with a circular interaction region.
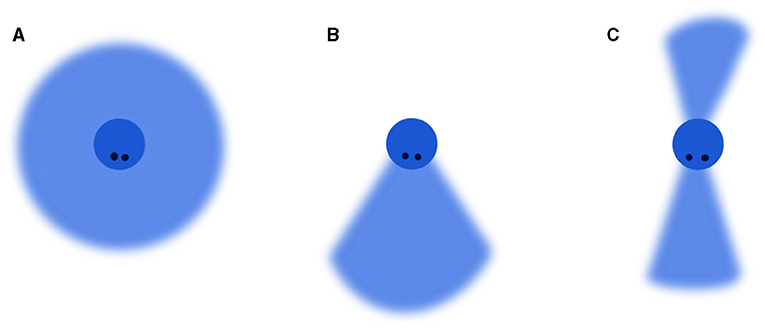
- Figure 2 - Common types of interaction regions used in different contexts.
- (A) A simple interaction region where Blake sees others all around. (B) An interaction region where Blake can only see in a cone in front of it. A region of this shape could be used to model drones with a fixed camera or sensor. (C) An interaction region where Blake can see ahead and behind it. A region of this shape could be used to model cars with rear-view mirrors driving on a highway.
So how does Blake use the interaction region? In the easiest case, when Blake does not see another particle, it simply moves in the direction it wants to go, like if it was moving in an empty hallway. On the other hand, if Blake sees another particle, it might want to make a change. What change? Good question! There are many choices Blake could make. It could speed up or slow down, run away from or run toward the other particle, switch places with a particle, or even teleport to a different location (though this one may not be so practical). There are so many possibilities! For now, we will say our particles do two things:
• Change their speed so they do not run into each other (Figure 3A) and
• Change the direction they are traveling to move away from others (Figure 3B).
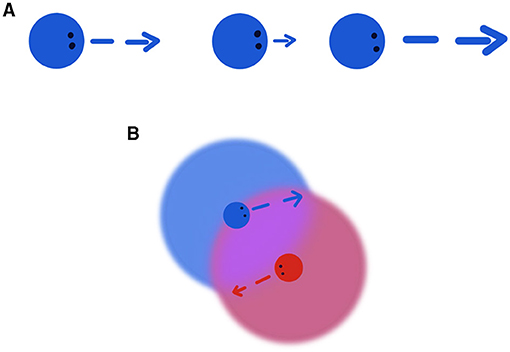
- Figure 3 - (A) When the particles cannot move to the side, they can adjust their speeds to avoid hitting each other.
- Here, the middle particle moves slower to avoid colliding with the particle in front of it. Meanwhile, the lead particle moves faster to avoid the particle behind it. (B) When two particles see each other, they can also adjust the direction of their movement to avoid colliding, while also still moving in their preferred direction.
Let us try to re-enact the experiment by saying that blue particles want to travel to the right and red particles to the left. So, they will choose a velocity that gets them closer to their goal without hitting other particles. When particles want to move away from other particles, it is called repulsion, and when they want to move toward other particles, it is called attraction. So, our particles are “repulsed” by others. Keep in mind that our particles do not know the other particles’ colors, they just want to get to the other end of the hallway.
Simulating Interacting Particle Systems
Now, let us see what happens when we put all of this together, in this video. What do you see? Did you notice that the people formed groups with members of the same color? The people do not know what colors the other people are, so this grouping is completely natural! It turns out it is always easier for people to move if they are in a group of people going in the same direction. Knowing this now, how might you try to walk in a crowded hallway?
Wrapping Up
So, what have we shown? From simple descriptions of individual dynamics, we can see that the interacting particle system can mimic real world experiments and even captures the emergence of complicated phenomena like lane formation. While this is a strong benefit to the method, there were many choices made. This leads to a world of “what if?” questions and so this field is actively explored in the engineering and mathematics community. The mathematics presented here also has many applications to biology and physics in fields such as cell-migration, animal flocking, and particle physics.
You may want to try to simulate your own system of particles. You could do so using the web platform Netlogo’s traffic simulation. You will not find a counter flow situation, but to start with, you could run the basic car traffic scenarios for a single lane and two lanes. You can also simulate one- and two-lane traffic flow online using the Complexity Explorables traffic simulation. Try changing the parameters and see what you find!
Glossary
Crowd Dynamics: ↑ A description of how a crowd and individuals within the crowd change over time.
Mathematical Model: ↑ A set of mathematical rules and equations which try to describe real world events.
Counter Flow: ↑ When people or cars move in opposite directions.
Particle: ↑ A small, single part of a bigger system, such as a person in a crowd or a car on the street.
Interaction Region: ↑ The space around a particle where interactions such as attraction and repulsion happen.
Velocity: ↑ The combination of a particle’s speed and direction of motion.
Repulsion: ↑ When a particle moves away from other particles in its interaction region.
Attraction: ↑ When a particle moves toward other particles in its interaction region.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The research activity of ME is funded by the European Union’s Horizon 2022 research and innovation program under the Marie Skłodowska-Curie fellowship project MATT (project no. 101061956).
References
[1] ↑ Cirillo, E. M. N., and Muntean, A. 2012. Can cooperation slow down emergency evacuations? Compt. Rendus Mecan. 340:625–628. doi: 10.1016/j.crme.2012.09.003
[2] ↑ Perkowitz, S. 2023. The Physics of Crowds. Available at: https://nautil.us/the-physics-of-crowds-388020/
[3] ↑ Corbetta, A., and Toschi, F. 2023. Physics of human crowds. Ann. Rev. Cond. Matter Phys. 14:311–333. doi: 10.1146/annurev-conmatphys-031620-100450
[4] ↑ Evers, J., and Muntean, A. 2011. Modeling micro-macro pedestrian counterflow in heterogeneous domains. Nonl. Phen. Complex Syst. 14:27–37.
[5] ↑ Xie, W., Lee, E. W. M., and Lee, Y. Y. 2022. Self-organisation phenomena in pedestrian counter flows and its modelling. Safety Sci. 155:105875. doi: 10.1016/j.ssci.2022.105875
