Abstract
Convex polygons, shapes bounded by straight lines in which all of the corners point outward, are the simplest of shapes, but despite their simplicity, there are many unsolved problems concerning polygons. Some polygons have the nice property that they fit together espcially well, so that you can use lots of copies of them to cover a large surface to form what is called a tiling. For some polygons, such as triangles, it is easy to see how to form tilings. For others, such as seven-sided convex polygons, it is impossible to form a tiling. This article discusses the history of a long-standing open question in geometry: which convex pentagons give rise to tilings of the plane? The authors also discuss their contribution to the solution of this problem, which involved developing a computerized algorithm to help them search for a new kind of convex pentagon that can form tilings, and the basic idea of this algorithm is discussed.
How Mathematical Discoveries Are Made!
Does it surprise you to hear that big, new discoveries in mathematics are being made all the time? Sometimes people think that mathematics mostly involves learning to use formulas discovered in ancient times, such as the Pythagorean theorem. While that is not true, mathematical discoveries can often be difficult to explain in nontechnical terms, and many times these discoveries do not have immediate real-world applications. Indeed, we (the authors) were unaware of new mathematical discoveries until we were college students, so we want to give you an insider’s view on how these discoveries can be made.
Like most new science, new mathematical discoveries are born out of curiosity about how the world works. We believe that developing habits of mind that lead to questioning why things are true and whether those truths can apply to new situations can lead to the discovery of new mathematics. People who want to discover new mathematics must be curious about why and how mathematics works, instead of just accepting facts without question! In that spirit, this article tells the story of our own mathematical discovery.
The Tiling Problem: What Shapes Can Cover The Plane Without Gaps or Overlaps?
Tilings are patterns formed from shapes that cover various kinds of surfaces. You have probably seen tiled kitchen floors and patios, or maybe more elaborate examples such as M.C. Escher’s artwork. Look around in your daily life, and you will likely see many tilings, as in Figures 1A–C. Tilings appear in the natural world, such as in a bee’s honeycomb, the cracked mud of a dried lake bottom, and a giraffe’s fur. They are even used to understand how the atoms of crystals fit together. Mathematicians have worked for many years to understand and classify various kinds of tilings.

- Figure 1 - Real-world tilings (A–C) and tilings of the plane (D, E).
- (A) Giraffe with tiling fur pattern. (B) Dried mud forms a tiling. (C) A mosaic pattern at the Alhambra. (D) A tiling by squares of 4 sizes. (E) A monohedral tiling. (F) A tiling by nonconvex polygons.
In geometry, the definition of a tiling is an arrangement of shapes that covers an entire flat surface that goes on forever in all directions, called a plane, without gaps or overlaps (Figures 1D–F). To understand the science of tilings, mathematicians are interested in the central question: “what shapes can be used to form tilings?” This is called The Tiling Problem. Because the shapes in tilings can be so varied (jagged, curvy, pointy, big, or small), it is impossible to answer this question without simplifying it.
To simplify The Tiling Problem so that we may hope to solve it, we must restrict the conditions of the problem in three ways. First, we require that all the individual tiles in the tilings have the same shape and size, meaning they are congruent. These are called monohedral tilings (Figures 1E, F). Second, we require that the single tile used to create the tiling be a polygon, which is a shape bounded by straight lines, like a triangle (three sides) or a pentagon (five sides). Last, we required that the polygon be convex, meaning its corners all point outward, as in Figure 1E. 3-sided polygons are called triangles; 4-sided polygons are quadrilaterals; 5-sided polygons are pentagons; 6-sided polygons are called hexagons; in general, polygons with n sides are called n-gons.
When we use these limitations, our simplified version of The Tiling Problem, called The Tiling Problem for Convex Polygons, asks: “Which convex polygons can be used to form monohedral tilings of the plane?” (You can try this for yourself by following the direction in Appendix A). The solution to The Tiling Problem for Convex Polygons has a rich history, spanning over 100 years and involving many people (Table 1). Some of the people who contributed to this problem’s solution were not professional mathematicians; they were just curious people who asked “Why?” We hope this encourages you to do so as well!

- Table 1 - History of the tiling problem for convex polygons until 1985.
Isohedral Tilings - Recipes For Tilings
Imagine that you have two copies of the same tiling, one lying on top of the other so that they are perfectly aligned. Now picture sliding the top copy in some direction so that the top copy again perfectly aligns with the bottom copy. Such a motion is called a symmetry of the tiling. Another way to understand the idea of a symmetry of a tiling is to think of a “before picture” and an “after picture”—if you slide a tiling and the before picture and the after picture are exactly the same, then the direction and distance that you slid the tiling is a symmetry of the tiling. To describe the complexity of the symmetries of a monohedral tiling, we can ask whether or not, for any two tiles in that tiling, there is a symmetry of the tiling that moves the first tile to the second tile. If the answer is yes, we say the tiling is isohedral.
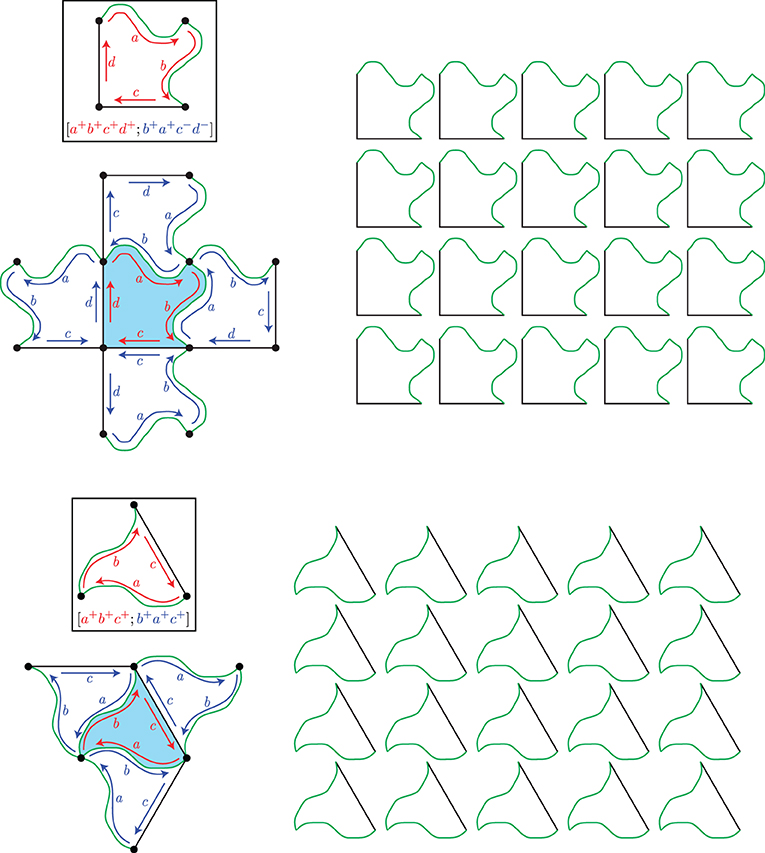
Isohedral tilings look the same around each tile, so we can understand how the shapes fit together in the whole tiling just by understanding what is happening around the boundary of any one tile. The way tiles fit around each other in an isohedral tiling is described by an incidence symbol, which can be viewed as a sort of recipe for how a shape can tile the plane (see Appendix B to explore the idea of incidence symbols.)
How We Found A New Type Of Pentagon
Led by our curiosity, we began to look for common features of the types of tilings known at the time (types 1–14 in Figure 2). We made two important observations, which generated even more questions!
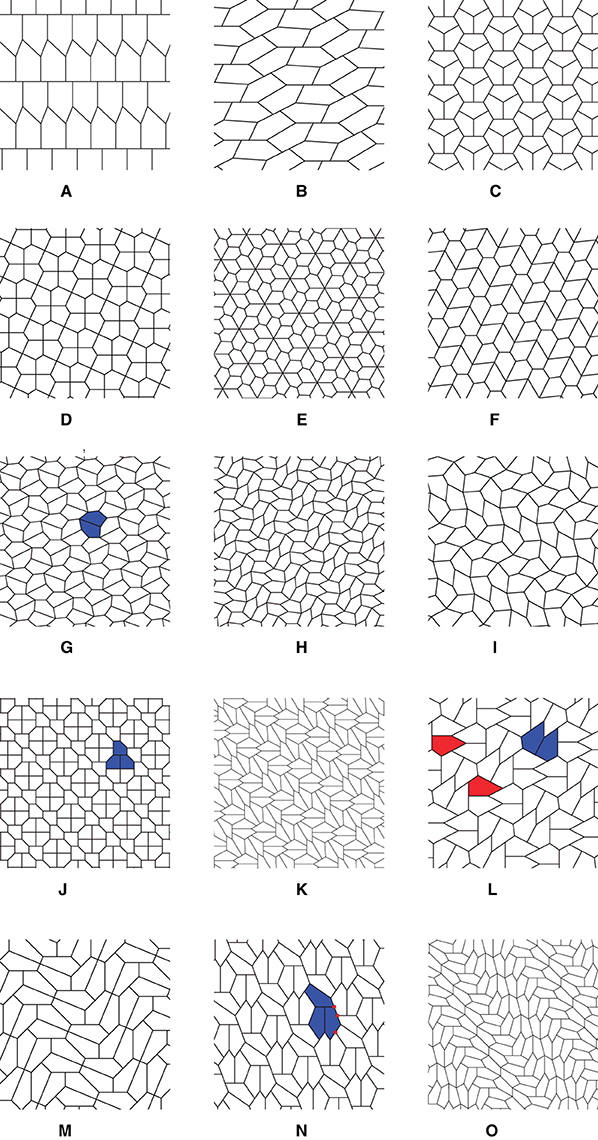
- Figure 2 - The 15 types of convex pentagons that can tessellate the plane.
- (A) Type 1: D + E = 180°. (B) Type 2: C + E = 180°; a = d. (C) Type 3: A = C = D = 120°; a = b,d = c + e. (D) Type 4: A = C = 90°; a = b,c = d. (E) Type 5: C = 2A = 90°; a = b, c = d. (F) Type 6: C + E = 180°, A = 2C; a = b = e,c = d. (G) Type 7: 2B + C = 360°, 2D + A = 360°; a = b = c = d. (H) Type 8: 2A + B = 360°, 2D + C = 360°; a = b = c = d. (I) Type 9: 2E + B = 360°, 2D + C = 360°; a = b = c = d. (J) Type 10: E = 90°, A + D = 180°, 2B - D = 180°, 2C + D = 360°; a = e = b + d. (K) Type 11: A = 90°, C + E = 180°, 2B + C = 360°; d = e = 2a + c. (L) Type 12: A = 90°, C + E = 180°, 2B + C = 360°; 2a = c + e = d. (M) Type 13: A = C = 90°, 2B = 2E = 360°- D; c = d, 2c = e. (N) Type 14: D = 90°, 2E + A = 360°, A + C = 180°; b = c = 2a = 2d. (O) Type 15: A = 60°, B = 135°, C = 105°, D = 90°, E = 150°; a = 2b = 2d = 2e.
First, types 1–5 can produce isohedral tilings. In types 6–14, if you cluster together two or three pentagons to act like a single tile, then that cluster produces an isohedral tiling; some types form tilings by clusters of two pentagons, as in Figures 2G, L, and others form tilings by clusters of three pentagons, as in Figures 2J, N. This observation guided us to consider how we might discover new convex pentagons that similarly tile the plane in isohedral clusters.
Our second observation was, along the boundaries of the clusters in tilings of types 6–14, we saw that the middle part of the edges of some pentagons met the corners of other pentagons, as illustrated by the red points in Figure 2N. We call these points flat nodes. We wondered how many flat nodes there might be in each cluster, and we proved that in tilings involving clusters of two pentagons, there can be at most two flat nodes per cluster. Similarly, in tilings involving clusters of three pentagons, there are at most three flat nodes. This was crucial to understanding all the possibilities.
Using these observations, we developed a computer algorithm to search for all possible pentagons that can produce these clustered tilings in which the sizes of the clusters are up to four. Type 15 (Figure 2O) was discovered through this computerized search. The algorithm works as follows. First, flat nodes are placed on the boundary of a template cluster of three pentagons. Second, an isohedral type was chosen for the cluster (out of 81 possible types) and the cluster was labeled according to the “recipe” for that isohedral type. Third, copies of the clusters were placed around a central copy of the cluster, according to the isohedral recipe. Fourth, the corners and sides of the individual pentagons of the clusters were labeled (there are many ways to do this, and the computer checks them all). Finally, from the resulting figure, equations describing the sides and angles of the pentagons were generated. The steps of this process are illustrated in Figure 3.
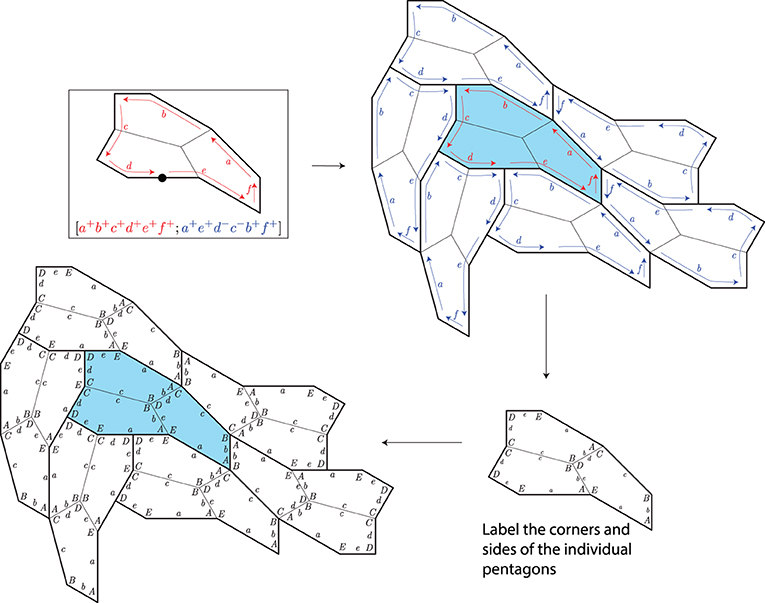
- Figure 3 - A 3-block cluster that generates an isohedral tiling.
- The red and blue labels and arrows indicate the incidence symbol [a+b+c+d+e+f+; a+e+d−c−b+f+]. To understand the incidence symbol, see Appendix B.
For the choice of labeling of pentagons at right in Figure 3, we see in the center of the figure that there are two corners labeled B and one corner labeled D; that arrangement gives us Equation 2B + D = 360°. We also see relationships among the sides; toward the middle of the figure, that b = d and b = e, and on the right side, taking into account the side labeled a extends over a flat node, we see that a = e + d. Writing down all such equations, we get the following equations:
These equations simplify those in Figure 2O. To justify this was a new type, we verified that we could make a pentagon with the specific angles and side lengths, and that such a pentagon did not satisfy any of the equations that define Types 1–14 (check for yourself!).
After our discovery of Type 15, French mathematician Micheal Rao heard the news and decided to investigate the problem. In doing so, he proved that the pentagon we discovered completed the classification, so types 1–15 form the complete classification of pentagons that tile the plane ([5]1), settling the longstanding Tiling Problem for Convex Polygons!
Summary
Often, in discovering new mathematical facts and theories, it truly “takes a village" in which individuals contribute in ways big and small to help solve a big problem, and this has certainly been the case with the tiling problem for convex polygons. Another important part of discovery is curiosity. We encourage you to always ask why whenever you encounter a new mathematical fact, formula, or procedure. Try to answer that question for yourself, because that is how we arrive at the new truths of mathematics and science.
Glossary
Tiling: ↑ A tiling of the plane to be an arrangement of shapes that covers the entire infinite 2-dimensional plane without gaps or overlaps.
Tiles: ↑ The individual shapes in a tiling are called tiles.
Monohedral Tilings: ↑ Tilings in which all of the tiles are congruent to one another are called monohedral tilings.
Triangles: ↑ 3-sided polygons are called triangles.
Quadrilaterals: ↑ 4-sided polygons are quadrilaterals.
Pentagons: ↑ 5-sided polygons are pentagons.
Hexagons: ↑ 6-sided polygons are called hexagons.
n-Gons: ↑ In general, polygons with n sides are called n-gons.
Convex Polygons: ↑ Shapes whose boundaries are straight line segments and whose corners all point outward are called convex polygons.
Symmetry: ↑ A symmetry of a tiling is a way to move a tiling so that the “before picture” and the “after picture” are identical.
Isohedral: ↑ If a monohedral tiling has the property that for any two tiles T1 and T2 in , there is a symmetry of that moves T1 to T2, we say is isohedral.
Flat Node: ↑ A flat node in a k-block transitive tiling by pentagons is a point on the boundary of a k-block where the corner of one pentagon meets a point in the middle of an edge of another pentagon.
k-Block Transitive: ↑ k-block transitive tilings are those in which identical clusters of k pentagons, acting as a single tile, form an isohedral tiling.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnote
1. ↑M. Rao posted an article on the online repository ArXiv, but the article has not yet been verified through a process of peer review.
References
[1] ↑ Reinhardt, K. 1918. Über die Zerlegung der Ebene in Polygone. Frankfurt: Univ. Frankfurt a.M. Noske.
[2] ↑ Kershner, R. B. 1968. On paving the plane. Am. Math Mon. 75:839–44.
[3] ↑ Niven, I. 1978. Convex polygons that cannot tile the plane. Am. Math. Mon. 85:785–92. doi: 10.2307/2320624
[4] ↑ Gardner, M. 1975. Mathematical games. Sci. Am. 233:112–9.
[5] ↑ Rao, M. 2017. Exhaustive search of convex pentagons which tile the plane. arXiv. doi: 10.48550/arXiv.1708.00274
Appendix A: Cut-Outs: Which of These Tiles Can Tessellate the Plane?
Directions: Cut out the individual shapes outlined in black and see if you can form tilings using copies of each kind of shape. You might find it easier if you use card stock instead of plain paper. Is a tiling possible or impossible, and why?
Appendix B. Cut-Outs: Isohedral Types
Directions: Cut out the shapes below and assemble them according to the incidence symbol. Lines or arcs of the same color fit together.