ملخص
المضلع المحدب هو شكل تحيطه خطوط مستقيمة وتتجه كل زواياه للخارج، وهو أبسط الأشكال. ولكن برغم هذه البساطة، فهناك العديد من المسائل المستعصية حول المضلعات. تتميز بعض المضلعات بأنها تتناسق معًا بشكل كبير للغاية لدرجة أنه يمكنك استخدام عدة نسخ منها لتغطية سطح كبير وتكوين ما يسمى بالتبليط. يسهل التبليط باستخدام بعض المضلعات، مثل المثلثات. ولكن هناك أنواع أخرى يستحيل استخدامها في التبليط مثل المضلعات السباعية المحدبة. يناقش هذا المقال تاريخ المسألة الهندسية المستعصية من وقت طويل، وهي: أي المضلعات الخماسية المحدبة يمكنها تبليط المستوى؟ يعرض المؤلفان أيضًا إسهامهما في حل هذه المسالة والذي تضمّن تطوير لوغاريتم عبر الكمبيوتر لمساعدتهما على البحث عن نوع جديد من المضلع الخماسي المحدب يمكنه تبليط المستوى، ويشرح المؤلفان أيضًا الفكرة الأساسية لهذا اللوغاريتم.
كيف يتم التوصل إلى اكتشافات الرياضيات؟
هل تعلم أن علماء الرياضيات يتوصلون إلى اكتشافات كبيرة جديدة طوال الوقت؟ يعتقد الناس أحيانًا أن الرياضيات تدور في الغالب حول تعلّم تطبيق الصيغ الرياضية التي تم اكتشافها في الماضي مثل نظرية فيثاغورس. وهذا غير صحيح، إلا أنه يصعب في أغلب الأحيان شرح الاكتشافات الرياضية باستخدام مصطلحات غير متخصصة، وفي أوقات كثيرة لا تتحقق تطبيقات فورية واقعية لهذه الاكتشافات. في الواقع، لم نكن نحن (المؤلفان) على علم بالاكتشافات الرياضية الجديدة إلى أن بدأنا المرحلة الجامعية ولذلك أردنا إعطاءك لمحة حول كيفية التوصل إلى هذه الاكتشافات.
على غرار أغلب العلوم الجديدة، فإن الدافع الأول لأحدث الاكتشافات الرياضية هو الفضول حول آلية عمل الكون. نعتقد أن تطوير عادات العقل أو التفكير التي تؤدي بك إلى الاستفسار عن سبب صحة الأشياء ومدى إمكانية تطبيق الحقائق على الأوضاع الجديدة يمكن أن يقودك إلى اكتشافات جديدة في عالم الرياضيات. ومن الصفات الأساسية في مكتشفي الرياضيات الفضول حول آلية عمل القواعد الرياضية وسببها بدلاً من التسليم بالحقائق دون أي سؤال. على هذا الأساس، سيناقش هذا المقال قصة اكتشافنا الرياضي.
مسألة التبليط: ما الأشكال التي يمكنها تغطية المستوى دون فجوات أو تداخلات؟
التبليط عبارة عن أنماط مكوّنة من أشكال تغطي أنواعًا متعددة من الأسطح. رأيت بالطبع من قبل أرضيات مطابخ وباحات مبلطة أو أمثلة أكثر تعقيدًا مثل الأعمال الفنية للرسام موريتس كورنيليس إيشر. ألق نظرة على محيطك اليومي وسترى العديد من أنواع التبليط، كما يظهر في الأشكال 1A–C. تضمّ الطبيعة كذلك أشكال تبليط متعددة، مثل خلايا النحل والتصدعات الطينية في قاع البحيرات الجافة وجلد الزرافة، بل وتُستخدم التبليطات أيضًا لفهم مدى تناسق ذرات الأشكال البلورية معًا. وقد اجتهد علماء الرياضيات عدة سنوات لفهم الأنواع المختلفة للتبليط وتسميتها.

- شكل 1 - أشكال تبليط من العالم الواقعي (A–C) وشكلان لتبليط المستوى (D, E).
- (A) زرافة بنمط جلد مبلّط (B) تصدع طيني جاف يكوّن شكل تبليط (C) نمط فسيفساء في قصر الحمراء (D) شكل مبلط يتكون من مربعات لها 4 أحجام (E) تبليط أحادي الشكل (F) تبليط يتكون من مضلعات غير محدبة
في الهندسة، التبليط عبارة عن ترتيب مكوّن من أشكال يمكنها تغطية سطح كامل مستوٍ لانهائي يُسمى بالمستوى بدون فجوات أو تداخلات (الشكلان 1D–F). ولفهم علم التبليط، يهتم علماء الرياضيات بسؤال محوري وهو: ''ما الأشكال التي يمكن استخدامها في التبليط؟'' وهذا ما يُسمى بمسألة التبليط. نظرًا لتنوع أشكال التبليط (مثل المتعرج والمنحني والمدبب والكبير والصغير)، تستحيل الإجابة عن هذا السؤال دون تبسيطه أولاً.
ولتبسيط مسألة التبليط حتى نحلها (نأمل ذلك)، يجب أن نقيد شروط المسألة بثلاث طرق. أولاً، لا بد أن تكون كل بلاطة في التبليط لها الشكل والحجم نفسهما، أي كل البلاط متطابق مع بعضه. وهذا ما يُسمى بالتبليط أحادي الشكل (الشكلان 1E, F). ثانيًا، يجب أن تكون كل بلاطة مُستخدمة في التبليط عبارة عن مضلع، وهو شكل تحيطه خطوط مستقيمة، ومن أمثلة ذلك المثلث (ثلاثة أضلاع) أو المضلع الخماسي (خمسة أضلاع). أخيرًا، يلزم أن يكون المضلع محدبًا، أي أن كل زواياه تتجه للخارج، تمامًا كما في الشكل 1E, F. المضلع المكون من 3 أضلاع يُسمى المثلث والمكون من 4 أضلاع يُسمى المضلع الرباعي والمكوّن من 5 أضلاع يُسمى المضلع الخماسي والمكوّن من 6 أضلاع يُسمى المضلع السداسي، أي أن الاسم يتكون من كلمة ''المضلع'' + الرقم مكتوبًا.
وبعد تحقيق هذه الشروط، نطرح السؤال التالي في نسختنا المبسطة من مسألة التبليط والتي نطلق عليها مسألة التبليط بالمضلعات المحدبة: ''ما المضلعات المحدبة التي يمكن استخدامها لتبليط المستوى بشكل أحادي؟'' (يمكنك تجربة ذلك بنفسك باتباع التوجيهات في الملحق أ). بدأ حل هذه المسألة من 100 سنة وشارك فيه العديد من الأشخاص (الجدول 1). ضمّت قائمة المساهمين في حل هذه المسألة أشخاصًا لم يكونوا علماء رياضيات محترفين، بل مجرد أشخاص دفعهم فضولهم إلى السؤال عن السبب. ونحن نأمل أن يشجعك ذلك أيضًا على حذو حذوهم.

- جدول 1 - تاريخ مسألة التبليط بالمضلعات المحدبة حتى عام 1985.
التبليط المتطابق المتعدي: وصفات للتبليط
تخيّل أن لديك نسختين من التبليط نفسه، واحدة موضوعة فوق الأخرى في توازٍ مثالي. تصوّر الآن تحريك النسخة العلوية في اتجاه معين بحيث تتوازى مرة أخرى تمامًا مع النسخة السفلية. تُسمى هذه الحركة تناظر التبليط. إليك طريقة أخرى لفهم فكرة تناظر التبليط. فكّر في التبليط ''قبل التحريك'' و''بعد التحريك''. إذا حركت تبليطًا ووجدته كما هو بالضبط قبل التحريك وبعده، فإن التبليط متناظر في هذا الاتجاه وعلى بُعد هذه المسافة. لوصف الطبيعة المعقدة لتناظرات التبليط أحادي الشكل، يمكننا أن نسأل إذا كان هناك تناظر بين أي بلاطتين في التبليط يحوّل البلاطة الأولى إلى الثانية. إذا كانت الإجابة نعم، فالتبليط متطابق ومتعدٍّ.
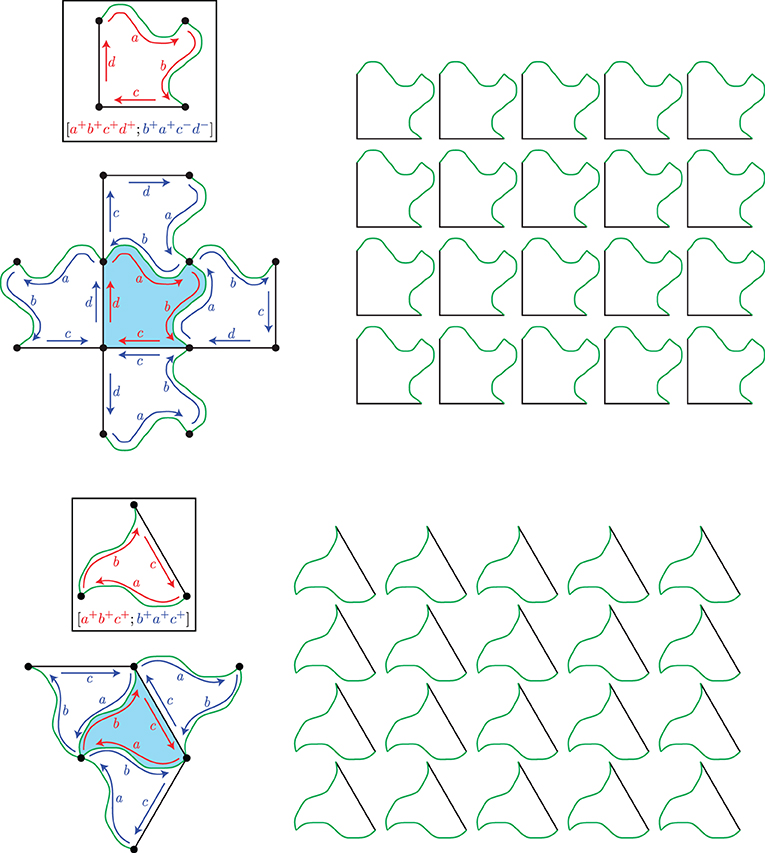
وهذا النوع من التبليط يبدو كما هو حول كل بلاطة، ولهذا يمكننا أن نفهم كيف تتناسق الأشكال معًا في التبليط ككل من مجرد فهم ما يحدث حول حدّ أي بلاطة. توصف الطريقة التي يتناسق بها البلاط حول بعضه في تبليط متطابق ومتعدٍّ برمز سقوط يمكن اعتباره كنوع من الوصفات لكيفية تبليط شكل ما للمستوى (انظر الملحق ب لاستكشاف فكرة رموز السقوط.)
كيف اكتشفنا نوعًا جديدًا من المضلع الخماسي؟
انطلاقًا من شعورنا بالفضول، بدأنا البحث عن الميزات المشتركة لأنواع التبليط المعروفة في الوقت الحالي (الأنواع 1-14 في الشكل 2). توصلنا إلى ملاحظتين مهمتين، ما أدى إلى المزيد من الأسئلة.
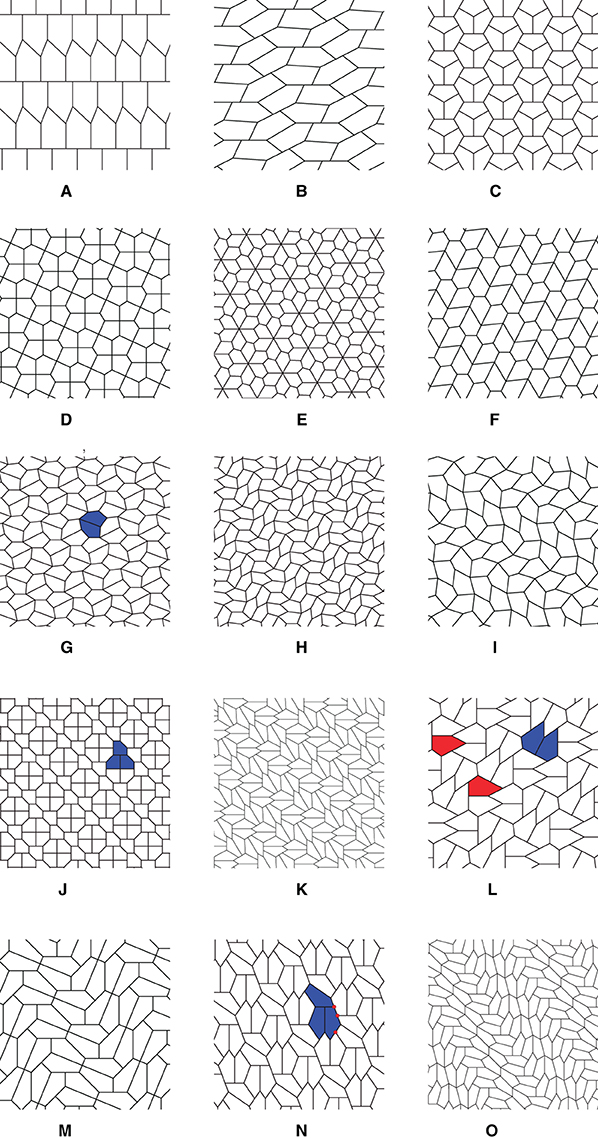
- شكل 2 - الأنواع الـ 15 من المضلعات الخماسية المحدبة التي يمكنها تبليط المستوى.
- (A) النوع 1:
- D + E = 180°. (B) النوع 2: C + E = 180°؛a = d.
- (C) النوع 3:◦
- A = C = D = 120؛ a = b، d = c + e. (D)
- النوع 4: A = C = 90°؛
- a = b، c = d. (E) النوع 5:
- C = 2A = 90°؛a = b،
- c = d. (F) النوع 6:
- C + E = 180°،= 2C A؛
- a = b = e، c = d. (G) النوع 7: 2B + C = 360°، 2D + A = 360°؛
- a = b = c = d. (H) النوع 8: 2A + B = 360°،
- 2D + C = 360°؛
- a = b = c = d. (I) النوع 9: 2E + B = 360°،
- 2D + C = 360°؛
- a = b = c = d. (J) النوع 10: E = 90°،
- A + D = 180°، 2B – D = 180°،
- 2C + D = 360°؛
- a = e = b + d. (K) النوع 11: A = 90°،
- C + E = 180°،2B + C = 360°؛
- d = e = 2a + c. (L) النوع 12: A = 90°،
- C + E = 180° ، 2B + C = 360°؛
- 2a = c + e = d. (M) النوع 13: A = C = 90°، 2B = 2E = 360° - D؛
- c = d ، 2c = e. (N) النوع 14: D = 90°،
- 2E + A = 360°،
- A + C = 180°؛
- b = c = 2a = 2d. (O)
- النوع 15: A = 60°،
- B = 135°،C = 105°،
- D = 90°،E = 150°؛
- a = 2b = 2d = 2e.
أولاً، يمكن للأنواع 1 إلى 5 إنتاج تبليط متطابق ومتعدٍّ. أما بالنسبة للأنواع 6 إلى 14، فإذا جمعت عدد 2 أو 3 من المضلعات الخماسية لتكوين بلاطة واحدة، تشكل هذه الوحدة تبليطًا متطابقًا ومتعديًا، بينما تنتج بعض الأنواع تبليطًا من خلال تشكيل وحدات يتألف كل منها من مضلعين خماسيين، كما في الشكلين 2G, L ول، وتكوّن أنواع أخرى التبليط من خلال وحدات مكوّنة من ثلاثة مضلعات خماسية كما في الشكلين 2J, N ون. قادتنا هذه الملاحظة إلى التفكير في كيفية اكتشاف أنواع جديدة من المضلعات الخماسية المحدبة والتي تبلط المستوى على نفس المنوال في شكل وحدات متطابقة ومتعدية.
أما الملاحظة الثانية، فكانت أننا رأينا على طول حدود الوحدات في أنواع التبليط 6-14 التقاء وسط حواف بعض المضلعات الخماسية بزوايا مضلعات خماسية أخرى كما هو موضح بالنقاط الحمراء في الشكل 2N. وأطلقنا على هذه النقاط اسم العُقد المسطحة. وتساءلنا عن عدد العُقد المسطحة في كل وحدة، فأثبتنا أنه في أشكال التبليط التي تضم وحدات مؤلفة من مضلعين خماسيين، يمكن أن توجد عقدتان مسطحتان على الأكثر في كل وحدة.
بالقياس نفسه، فإن التبليط ذي الوحدات المؤلفة من ثلاثة مضلعات خماسية يشتمل على ثلاث عُقد مسطحة على الأكثر. ساعدنا ذلك كثيرًا في فهم كل الاحتمالات.
باستخدام هاتين الملاحظتين، طوّرنا لوغاريتم بالكمبيوتر للبحث عن كل المضلعات الخماسية المحتملة التي يمكنها إنتاج هذه التبليطات حيث توجد 4 أحجام وحدات بحد أقصى. تم اكتشاف النوع 15 (الشكل 2O) من خلال هذا البحث المدار بالكمبيوتر. يعمل اللوغاريتم على الشكل التالي: أولاً، توضع العُقد المسطحة على حد نموذج وحدة مكوّنة من ثلاثة مضلعات خماسية.
ثانيًا، يتم اختيار نوع التبليط المتطابق والمتعدي للوحدة (من أصل 81 نوعًا محتملاً) وتتم تسمية الوحدة وفقًا لـ ''وصفة'' هذا النوع. ثالثًا، توضع نُسخ من الوحدات حول نسخة وسطى من الوحدة المختارة وفقًا لوصفة التبليط المتطابق والمتعدي. رابعًا، تتم تسمية زوايا وأضلاع المضلعات الخماسية الفردية في الوحدات (تتعدد طرق ذلك، ويتحقق الكمبيوتر منها جميعًا). أخيرًا، يتم استخدام الشكل الناتج لصياغة المعادلات التي تصف أضلاع وزوايا المضلعات الخماسية. يوضح الشكل 3 خطوات هذه العملية.
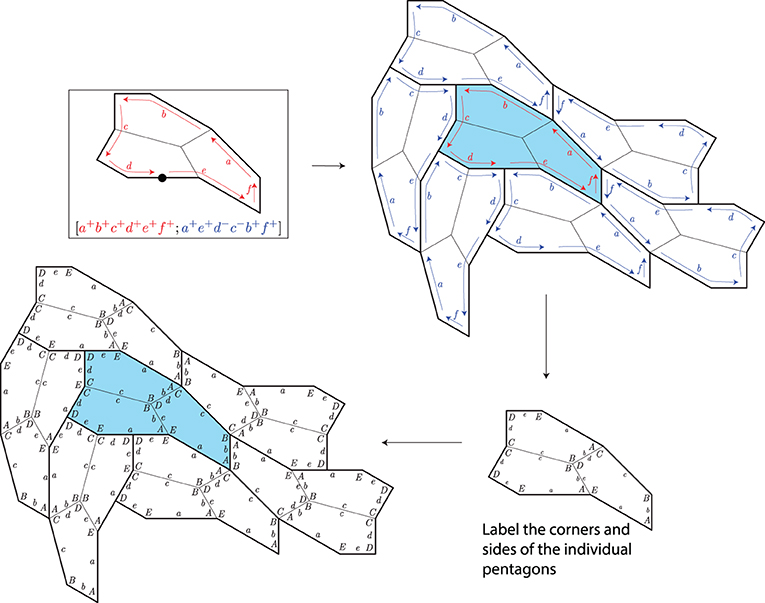
- شكل 3 - وحدة مكونة من 3 أجزاء تشكّل تبليطًا متطابقًا ومتعديًا.
- تشير التسميات والأسهم الحمراء والزرقاء إلى رمز السقوط [a+b+c+d+ e+f+: a+e+d−c−b+f+]. لفهم رمز السقوط، انظر الملحق ب.
بالنسبة لاختيار تسميات المضلعات الخماسية على اليمين في الشكل 3، لاحظنا أنه في منتصف الشكل توجد زاويتان مسميتان B وزاوية مسماة D ما يعطينا المعادلة: 2B + D = 360°. وجدنا أيضًا علاقات بين الأضلاع، فباتجاه منتصف الشكل، لاحظنا ما يلي: b = d وb = e وعلى الجانب الأيمن: a = e + d (لاحظ أن الضلع المسمى a يمتد بطول عقدة مسطحة). وبعد تدوين كل هذه المعادلات، توصلنا إلى ما يلي:
وهذه المعادلات تبسّط تلك الموضحة في الشكل 2O. لإثبات أن هذا نوع جديد، تأكّدنا من أنه يمكننا إنشاء مضلع خماسي بأطوال الأضلاع والزوايا المحددة وأن مثل هذا المضلع الخماسي لا ينطبق على أي من المعادلات المعرّفة للأنواع 1-14 (يمكنك التأكّد بنفسك).
بعد اكتشافنا للنوع 15، سمع عالم الرياضيات الفرنسي ''مايكل راو'' بالأخبار وقرر البحث في المسألة. وعند القيام بذلك، أثبت أن المضلع الخماسي الذي اكتشفناه أكمل التصنيف، وبالتالي تشكل الأنواع 1-15 التصنيف الكامل للمضلعات الخماسية التي تبلط المستوى ([5]1)، وبهذا اكتمل حلّ مسألة التبليط بالمضلعات المحدبة التي ظلت مستعصية لمدة طويلة.
الملخص
في أغلب الأحيان، يتطلب اكتشاف الحقائق والنظريات الرياضية الجديدة ''مجهودًا جماعيًا'' يساهم فيه كل فرد بأي مساهمة كبيرة كانت أو صغيرة للمساعدة في حل مسألة كبيرة، وهذا ما حدث بالتأكيد في مسألة التبليط بالمضلعات المحدبة. الشق الآخر المهم من كل اكتشاف هو الفضول. ولذلك نحثك على عدم التسليم الفوري بأي حقيقة أو صيغة أو عملية رياضية جديدة بل الاستفسار عن السبب دائمًا. حاول الإجابة عن ذلك السؤال بنفسك لأن هذا ما يساعدنا في التوصل إلى الحقائق الجديدة في الرياضيات والعلوم.
مسرد للمصطلحات
التبليط (TILING): ↑ تبليط المستوى هو ترتيب مكوّن من أشكال يغطي كامل المستوى اللانهائي ثنائي الأبعاد دون فجوات أو تداخلات.
البلاطة (TILES): ↑ كل وحدة في التبليط تُسمى بلاطة.
التبليط أحادي الشكل (MONOHEDRAL TILINGS): ↑ نمط تبليط يكون فيه كل البلاط متطابق مع بعضه.
المثلث (TRIANGLES): ↑ شكل مكوّن من ثلاثة أضلاع.
المضلع الرباعي (QUADRILATERALS): ↑ شكل مكوّن من أربعة أضلاع.
المضلع الخماسي (PENTAGONS): ↑ شكل مكوّن من خمسة أضلاع.
المضلع السداسي (HEXAGONS): ↑ شكل مكوّن من ستة أضلاع.
المضلعات (n-GONS): ↑ تتكون المضلعات من عدد من الأضلاع وتتم تسميتها كالتالي: كلمة ''المضلع'' + الرقم مكتوبًا.
المضلع المحدب (CONVEX POLYGONS): ↑ أشكال تكون حدودها قطع خطوط مستقيمة وتتجه كل زواياها للخارج.
التناظر (SYMMETRY): ↑ تناظر التبليط هو طريقة لتحريك تبليط بحيث يتطابق قبل هذا التحريك وبعده.
التطابق والتعدي (ISOHEDRAL): ↑ إذا كان التبليط أحادي الشكل T يتسم بأنه بين أي بلاطتين T1 وT2 في T، هناك تناظر T يحوّل T1 إلى T2، فإذًا التبليط T متطابق ومتعدٍ.
العقدة المسطحة (FLAT NODE): ↑ العقدة المسطحة في أي تبليط متعدٍ يتكون من عدد (k) من الأجزاء المضلعة الخماسية هي نقطة على الحد تلتقي عندها زاوية مضلع خماسي مع نقطة في وسط حافة مضلع خماسي آخر.
تعدي الأجزاء المضلعة الخماسية (K-BLOCK TRANSITIVE): ↑ التبليط المتعدي المكوّن من أجزاء مضلعة خماسية هو ذلك النوع الذي تنتج فيه وحدات متماثلة من المضلعات الخماسية (تمثّل ككل بلاطة واحدة) تبليطًا متطابقًا متعديًا.
إقرار تضارب المصالح
يعلن المؤلفون أن البحث قد أُجري في غياب أي علاقات تجارية أو مالية يمكن تفسيرها على أنها تضارب محتمل في المصالح.
Footnote
1. ↑نشر ''مايكل راو'' مقالاً على مستودع ArXiv الإلكتروني ولكن لم يخضع بعد لعملية مراجعة الأقران.
المراجع
[1] ↑ Reinhardt, K. 1918. Über die Zerlegung der Ebene in Polygone. Frankfurt: Univ. Frankfurt a.M. Noske.
[2] ↑ Kershner, R. B. 1968. On paving the plane. Am. Math Mon. 75:839–44.
[3] ↑ Niven, I. 1978. Convex polygons that cannot tile the plane. Am. Math. Mon. 85:785–92. doi: 10.2307/2320624
[4] ↑ Gardner, M. 1975. Mathematical games. Sci. Am. 233:112–9.
[5] ↑ Rao, M. 2017. Exhaustive search of convex pentagons which tile the plane. arXiv. doi: 10.48550/arXiv.1708.00274
الملحق أ: نشاط قصّ الأشكال: أيّ من البلاط التالي يمكنه تغطية المستوى؟
التوجيهات: قصّ الأشكال الفردية المحددة باللون الأسود وجرّب إذا كان يمكنك تشكيل تبليط باستخدام نسخ من كل نوع من الأشكال. قد يسهل هذا النشاط أكثر إذا استخدمت الورق المقوى بدلاً من الورق العادي. هل تشكيل التبليط ممكن أم مستحيل، ولماذا؟
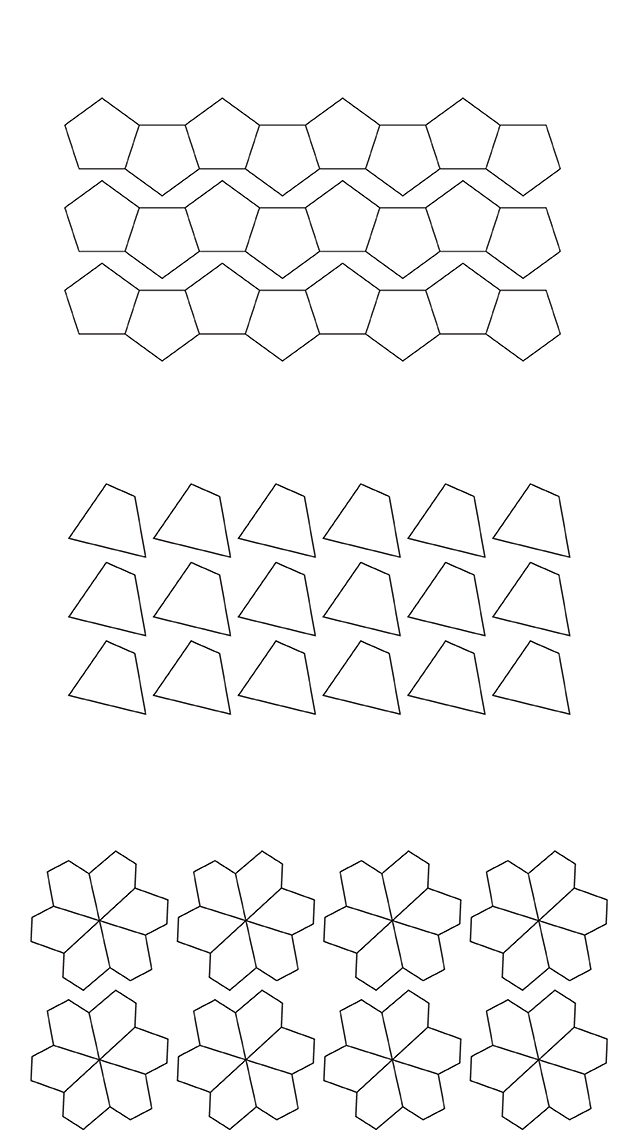
نشاط قصّ الأشكال في الملحق ب: أنواع التبليط المتطابق والمتعدي
التوجيهات: قصّ الأشكال التالية وركّبها معًا باستخدام رمز السقوط. الخطوط أو الأقواس من نفس اللون تتناسق معًا.