Abstract
Mechanical meta-materials are 3D-printed flexible structures produced from smaller units arranged in repeating patterns. The shape and organization of these repeating patterns determine how the materials will behave when we press on them. If the individual units are arranged following all the rules for how they like to change shape, the material can deform easily when we press on it. However, if the units are arranged such that they cannot all simultaneously change shape the way they like, the material is frustrated, and it will be harder for us to deform it. By designing the structure of meta-materials, we can control their degree of frustration and even design materials that will deform to any pattern we would like! Materials designed to deform in a specific way could be used to develop important new technologies that could help many people and may even reduce our use of earth’s precious natural resources.
How Can a Material Be Frustrated?!
When you hear the word frustration, you probably think of that upset or annoyed feeling you get when you are having trouble doing something, like completing your math homework or leveling up in a difficult computer game. But did you know that certain non-living materials can experience frustration, too? That is not all—we can use that frustration to design materials with extremely interesting and special qualities!
Many materials in nature are crystalline, meaning that the particles that make up the material are organized in a structured, repeating way, such as a square lattice (Figure 1A). Often, neighboring particles want to be in opposite states—for example, positive or negative electrical charges, or magnetic polarity pointing to the north or south. In the square lattice shown here, if the red and blue balls represent the two opposite states, you can see that it is easy to make sure no two neighboring balls are the same color if they are placed alternately, like the arrangement of black and white squares on a checkerboard. In contrast, in a triangular lattice (Figure 1B), once we place two balls with different colors in a single triangle, the third ball will be frustrated, because it can not “follow the rules.” It will want to be blue, to be different from its red neighbor, but it will also want to be red, to be different from its blue neighbor! No matter how hard we (or the laws of nature) try to make all the particles “happy,” in a large triangular lattice there will always be many particles that are frustrated [1, 2].
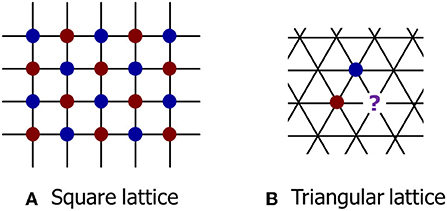
- Figure 1 - (A) In a square lattice, it is possible to please all particles by surrounding each particle with neighbors that are in the opposite state (like electrical charge or magnetic polarity).
- (B) In contrast, in a triangular lattice, once we please two particles, the third particle will be frustrated because it is unable to be in a different state from both of its neighbors.
Studying Frustrated Materials
Frustrated materials behave very differently from non-frustrated materials, and we would like to better understand why. It is generally hard for us to study the behaviors of individual particles in a material because these particles, called atoms, are very small. Usually, the distance between neighboring atoms in a solid is about one Angstrom (Å), which is a tenth of a billionth of a meter! This means that in one meter there are 10,000,000,000 Å.
Luckily, the many atoms that make up a normal material usually behave very similarly to one another, so it is often possible to understand the behavior of materials without seeing the exact state of each of its particles. To more easily study what is happening in materials, we create 3D-printed structures made of large “particles” that are easy to see, in which the distances between neighboring “particles” are centimeters, not Angstroms. We call these structures meta-materials, since they may be thought of as a material which is made up of material. Our work not only helps to understand frustrated materials, but it also allows us to design meta-materials with special, controllable properties, which we will explain soon.
Crystals in nature are composed of a unit cell, which is a certain pattern that repeats itself to create the material. The characteristics of a material are determined by both the structure and composition of its unit cells, and by the way those unit cells are arranged next to each other. Since we design our meta-materials, we can build any unit cell we want, and we can also arrange many unit cells side by side in different ways. For example, consider the rubber brick shown in Figure 2A. If we press on it, it will deform into one of the shapes shown in Figure 2B, based on the direction of pressing. When we combine many of these rubber bricks, we build what we will call a meta-cube, but we can rotate the bricks so that they lie in different directions within the cube [3]. We want to understand how the directions of different bricks inside our meta-material determine the way that the meta-material will deform when we press on it.
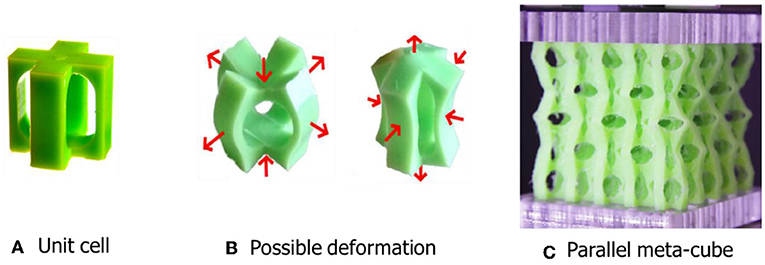
- Figure 2 - (A) Our meta-cubes are composed of pieces called unit cells.
- (B) The unit cells can be easily deformed in one of two directions, by putting pressure on the top and bottom or on the sides. (C) When all the unit cells are organized in the same direction, we get a parallel meta-cube in which the unit cells can alternately deform in these two ways (Adapted from Coulais et al. [3]).
We will start with a parallel meta-cube, in which all the bricks are organized in the direction shown in Figure 2A. When that meta-cube is compressed from the top and bottom, the bricks constituting the meta-cube alternately deform into one of the two shapes in Figure 2B. In each face of the compressed meta-cube, one brick is sticking out and there is an indentation in the neighboring brick (Figure 2C). This means that there is compatibility in the organization of the bricks making up the meta-cube. But what happens if the meta-cube is not organized, meaning that each brick is placed in a different direction?
Let us look at a simplified structure consisting of four bricks attached to one another in a square (Figure 3A). As shown in the figure key, the colors correspond to the direction in which each brick was oriented in the square. If we push or pull on a chosen face of this four-block square, we can observe how the rest of the faces deform. The square shown in Figure 3A, is not frustrated. In contrast, no matter how we put pressure on the square in Figure 3B, there will always be at least one frustrated face. The brick in one side of this face wants that face to move in one direction, but the brick on the other side of that face wants it to move in the opposite direction. Frustration in the meta-cube makes it more rigid compared to a non-frustrated, or compatible meta-cube, since a larger force must be applied to overcome the frustration and deform it.
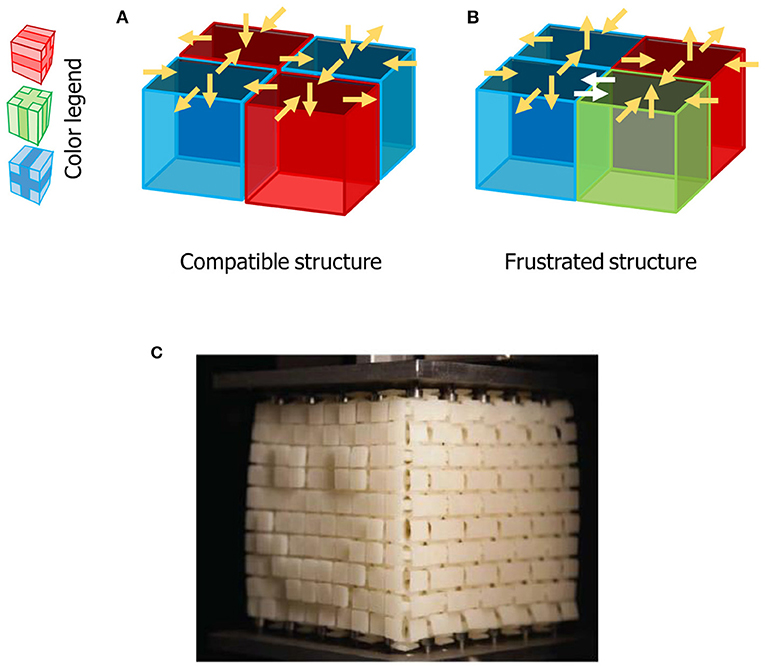
- Figure 3 - (A) When unit cells are arranged into a compatible structure, it is possible to please all of them simultaneously and the structure is easy to compress.
- This is shown by the yellow arrows that indicate the direction of deflection of each face. (B) If unit cells are arranged such that not all of them may be pleased at the same time, at least one face of the structure will be frustrated. This conflict is shown by the double white arrows, where there is competition between opposite directions of deflection. This will make the material more rigid. The colors of the cubes indicate the direction in which each unit cell is placed. (C) We designed a meta-cube to deform to a desired pattern (smiley face) when pressed (Adapted from Coulais et al. [3]).
Compatible Meta-materials: Pressing the Right Places
To analyze all possible meta-cubes, including those that are composed of many more than four bricks, we built a mathematical model, which describes whether any given meta-cube is frustrated or not. Our model allowed us to identify all compatible meta-cubes, meaning the ones that can deform without frustration in any of their unit cells. Using this model, we discovered that the number of compatible meta-cubes is huge! So huge, in fact, that we can design a meta-cube that will give us any pattern of deformation that we want on one face of the material. For example, we designed the meta-cube shown in Figure 3C so that, when we press on it from the top and bottom, it will deform with bumps and indentations that create a smiley face on its front1. If we press on its front in the same specific pattern of a smiley face, the meta-cube will deform relatively easily. In contrast, if we press on it with a different pattern, like a flat pattern, for example, it will be more difficult to deform this meta-material. Our mathematical model allows us to predict how the rigidity of the meta-cube will increase depending on the frustration we cause by the pressing pattern we use. In other words, we showed that the ability to deform a meta-material depends not only on the strength with which we press on it or the type of rubber from which the meta-cube was made, but also on the compatibility between the pattern with which we press the structure and the unique structure of that meta-cube.
What Can Meta-materials Be Used for?
The meta-cubes we developed are an interesting system that we can use to study compatibility and frustration occurring in a material. By combining identical repeating bricks oriented in various directions into big meta-cubes, we can design materials that deform in a specific way when they are under pressure. The ability to control the way a material deforms could be useful in various types of technologies. For example, imagine a robot that could change the rigidity of its arm to grab things more efficiently. Alternatively, these materials could be used to create medical implants or prosthetic legs that are perfectly suited to the bodies to which they are attached. Using meta-materials could also decrease our use of earth’s precious natural resources. So, now you can see that meta-materials are not only interesting materials that can teach us about frustration, but they may also be useful for improving people’s lives and the health of the planet!
Funding
This research was partially funded by the Israel Science Foundation and by the Netherlands Organisation for Scientific Research.
Glossary
Frustration: ↑ The inability to simultaneously fulfill a number of conflicting requirements [https://en.wikipedia.org/wiki/Geometrical_frustration].
Crystal: ↑ A solid material whose constituents are arranged in an ordered manner [https://en.wikipedia.org/wiki/Crystal].
Lattice: ↑ A repeating structure that looks the same after you move in different directions [https://en.wikipedia.org/wiki/Bravais_lattice].
Atom: ↑ The smallest unit of ordinary matter that forms a chemical element [https://en.wikipedia.org/wiki/Atom].
Meta-material: ↑ An artificial material whose characteristics depend mainly on the engineered structure of the cells that constitute it [https://en.wikipedia.org/wiki/Metamaterial].
Unit Cell: ↑ A pattern that repeats itself to make up a crystalline material [https://en.wikipedia.org/wiki/Unit_cell].
Meta-cube: ↑ A meta-material made of repeating cubic units oriented in different directions.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgment
The author thanks Yaara Shokef and Chaviva Sirote for helpful comments and suggestions regarding the writing and presentation of this article.
Footnote
1. ↑https://www.youtube.com/watch?v=NxcCtimWxn0 Combinatorial Design of Textured Mechanical Metamaterials.
Original Source Article
↑Coulais, C., Teomy, E., de Reus, F., Shokef, Y., and van Hecke, M. 2016. Combinatorial design of textured mechanical metamaterials. Nature. 535:529–532. doi: 10.1038/nature18960
References
[1] ↑ Wannier, G. H. 1950. Antiferromagnetism: the triangular Ising net. Phys. Rev. 79:357–364. doi: 10.1103/PhysRev.79.357
[2] ↑ Han, Y., Shokef, Y., Alsayed, A. M., Yunker, P., Lubensky, T. C., and Yodh, A. G. 2008. Geometric frustration in buckled colloidal monolayers. Nature. 456:898–903. doi: 10.1038/nature07595
[3] ↑ Coulais, C., Teomy, E., de Reus, F., Shokef, Y., and van Hecke, M. 2016. Combinatorial design of textured mechanical metamaterials. Nature. 535:529–532. doi: 10.1038/nature18960
