תַקצִיר
מֶטָא-חומרים מכניים הם מבנים גמישים המודפסים במדפסות תלת-ממד, עשויים יחידות קטנות יותר המאורגנות בתבניות החוזרות על עצמן. צורת התבניות והאופן שבו הן מסודרות במרחב קובעים איך החומר יתנהג כאשר נלחץ עליו. אם כל היחידות בחומר מאורגנות לפי הכללים התואמים לאופן שבו הן רוצות לשנות צורה, החומר יוכל להתעוות בקלות כאשר נלחץ עליו. לעומת זאת, אם היחידות מסודרות כך שלא כולן יכולות לשנות צורה בו זמנית באופן שבו שהן היו רוצות, החומר מתוסכל, ויהיה קשה יותר לעוות אותו. על ידי תכנון המבנה של מטא-חומרים ביכולתנו לשלוט במידת התסכול שלהם, ואפילו לְעַצֵּב חומרים שיתעוותו לכדי כל תבנית שנבחר! בחומרים המתוכננים להתעוות בצורה מסוימת ניתן להשתמש לפיתוח טכנולוגיות חשובות חדשות שיוכלו לסייע לאנשים רבים. טכנולוגיות אלה עשויות אף להפחית את השימוש שאנו עושים במשאבי הטבע היקרים של כדור הארץ.
כיצד חומר יכול להיות מתוסכל?!
כאשר אתם שומעים את המילה תסכול, ודאי מתעוררת בכם מחשבה לגבי תחושת הכעס או העצבנות המציפה אתכם כשאתם מתקשים בביצוע משימה כלשהי, כמו לסיים את שיעורי הבית במתמטיקה, או להתקדם שלב במשחק מחשב מאתגר. אבל האם ידעתם כי ישנם חומרים דוממים היכולים אף הם לחוות תסכול? יתרה מזו, באפשרותנו להשתמש בתסכול הזה בשביל לתכנן חומרים בעלי תכונות מעניינות ומיוחדות ביותר!
חומרים רבים בטבע הם גבישים, כלומר החלקיקים המרכיבים אותם מסודרים במבנה שחוזר על עצמו, כמו למשל בסָרִיג הריבועי (איור 1A). לעיתים קרובות, חלקיקים סמוכים רוצים להיות במצבים מנוגדים – לדוגמה, מִטענים חשמליים חיובים ושליליים, או קיטוב מגנטי המצביע צפונה או דרומה. בסריג הריבועי המוצג באיור, הכדורים האדומים והכחולים מייצגים את שני המצבים המנוגדים האלה. ניתן לוודא בקלות שאין שני כדורים סמוכים באותו הצבע כאשר ממקמים אותם לסירוגין, כמו סידור המשבצות הלבנות והשחורות בלוח שחמט. לעומת זאת, בסריג משולש (איור 1B), אחרי שמיקמנו שני כדורים בעלי צבעים שונים במשולש בודד בסריג, הכדור השלישי שנמקם יהיה מתוסכל, בגלל שהוא לא יכול לקיים את הכללים. הוא יִרְצֶה להיות כחול כדי להיות שונה מהשכן האדום שלו, אך גם ירצה להיות אדום, כדי להיות שונה משכנו הכחול! לא משנה עד כמה אנו (או חוקי הטבע) ננסה לְרַצּוֹת את כל החלקיקים הללו, בסריג משולש גדול, תמיד יהיו הרבה חלקיקים מתוסכלים [2, 1].
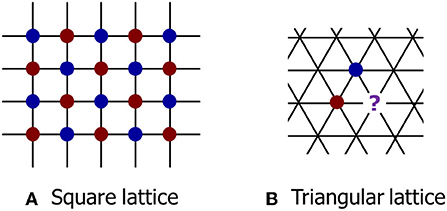
- איור 1 - השוני בין סריג ריבועי לסריג משולש.
- A. בסריג ריבועי, ניתן לְרַצּוֹת את כל החלקיקים על ידי הקפת כל חלקיק בחלקיקים במצב המנוגד (בדומה למִטען חשמלי או לקיטוב מגנטי). B. לעומת זאת בסריג משולש, לאחר שנְרַצֶּה שני חלקיקים, החלקיק השלישי שנמקם יהיה מתוסכל, משום שלא יוכל להיות במצב שונה משני שכניו.
חקירת חומרים מתוסכלים
חומרים מתוסכלים מתנהגים באופן שונה מאוד מחומרים שאינם מתוסכלים, והיינו מעוניינים להבין טוב יותר מדוע. באופן כללי, קשה לנו לחקור את ההתנהגויות של חלקיקים בודדים בחומר נתון, כיוון שחלקיקים אלה, הנקראים אטוֹמים, הם זעירים. בדרך כלל, המרחקים בין אטומים סמוכים בחומר מוצק הם מִסֵּדֶר גודל של אַנְגְסְטְרֶם (Å) אחד, שהוא עשירית המיליארדית של המטר! כלומר, במטר אחד ישנם 10,000,000,000 אנגסטרמים.
למרבה המזל, האטומים הרבים שמרכיבים חומר רגיל מתנהגים בדרך כלל בצורה דומה מאוד זה לזה. לכן, לרוב ניתן להבין את ההתנהגות של חומרים גם בלי לראות את המצב המדויק של כל חלקיק וחלקיק בתוכם. בשביל לחקור בקלות רבה יותר מה מתרחש בתוך חומרים, אנו יוצרים מבנים בהדפסת תלת-ממד העשויים ’חלקיקים‘ גדולים, שניתן לראות בקלות. במבנים אלה המרחקים בין ’חלקיקים‘ שכנים הם סנטימטרים, ולא אנגסטרמים. אנו מכנים את המבנים האלה מֶטָא-חומרים, בגלל שאפשר לחשוב עליהם כחומר העשוי מחומר. העבודה שלנו לא רק מסייעת בהֲבָנַת חומרים מתוסכלים; היא גם מאפשרת לנו לתכנן מטא-חומרים בעלי תכונות מיוחדות ונשלטות, שעל אודותיהם נפרט בהמשך המאמר.
גבישים בטבע מורכבים מתא יחידה. זוהי תבנית מסוימת החוזרת על עצמה במרחב ליצירת החומר. התכונות של כל חומר נקבעות הן על ידי מבנה תאי היחידה שלו והרכּבו, והן על ידי האופן שבו תאי היחידה מסודרים זה לצד זה במרחב. אנו מְעַצְּבִים את המטא-חומרים שלנו, ולכן יכולים לבנות איזה תא יחידה שנִרצה. באפשרותנו גם לְסַדֵּר תאי יחידה רבים זה לצד זה בצורות שונות. נסתכל למשל על לִבְנַת-הגומי שבאיור 2A. אם נלחץ עליה, היא תתעוות לאחת מהצורות המוצגות באיור 2B, בהתאם לכיוון שממנו נלחץ. כאשר אנו משלבים לבני-גומי רבות כאלה, אנו מרכיבים מבנה לו נקרא מֶטָא-קובייה. ביכולתנו לסובב את הלְּבֵנים כך שיִפנו לכיוונים שונים בתוך הקובייה [3]. אנו מעוניינים להבין כיצד הכיוונים של הַלְּבֵנים השונות בתוך המטא-חומר שבָּנִינוּ קובעים את האופן שבו המטא-חומר יתעוות כאשר נלחץ עליו.
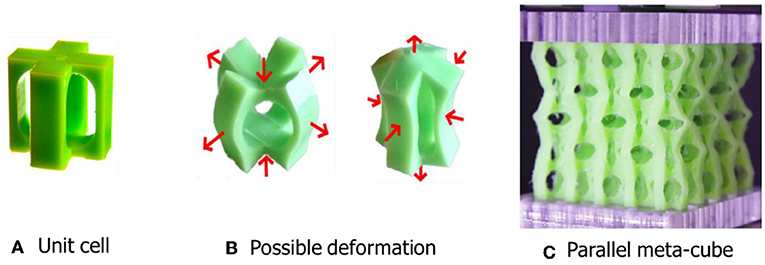
- איור 2 - המבנה המיוחד של מטא-קובייה.
- A. מטא-קוביות מורכבות מחלקים הנקראים תאי יחידה. B. תאי יחידה יכולים להתעוות בקלות באחד משני אופנִים: כאשר מפעילים לחץ מלמעלה ומלמטה, או לחלופין, בהפעלת לחץ מהצדדים. C. כאשר כל תאי היחידה מאורגנים באותו כיוון, מתקבלת מטא-קובייה מקבילה, שבה תאי היחידה יכולים להתעוות לסירוגין בשני האופנים הללו (האיור אומץ מ-Coulais ושותפים [3]).
נתחיל עם מטא-קובייה מקבילה, שבּה כל הלבֵנים מסודרות בכיוון המוצג באיור 2A. כאשר לוחצים על המטא-קובייה מלמעלה ומלמטה, הלבנים המרכיבות אותה מתעוותות לסירוגין לאחת משתי הצורות המוצגות באיור 2B. בכל פאה בתוך המטא-קובייה הדחוסה, לבנה אחת בולטת, ובלבנה השכנה נוצר שֶׁקַע (איור 2C). מכך ניתן להסיק כי ישנהּ תְּאִימוּת בסידור של הלבנים המרכיבות את המטא-קובייה. אבל מה קורה אם המטא-קובייה לא מסודרת, כלומר כל לבנה מוצבת בכיוון אחר?
נסתכל על מבנה פשוט המורכב מארבע לבנים המוצמדות זו לזו בריבוע (איור 3A). כפי שניתן לראות במקרא הצבעים באיור 3, כל צבע מייצג את הכיוון שאליו הלבנה פונה בריבוע. אם אנו דוחפים פאה אחת בריבוע בן ארבע הלבנים הזה, או מושכים אותה, נוכל לבחון כיצד שאר הפאות מתעוותות. הריבוע המוצג באיור 3A לא מתוסכל. לעומת זאת לא משנה מאיזה כיוון נפעיל לחץ על הריבוע המוצג באיור 3B, תמיד תהיה לפחות פאה אחת מתוסכלת. הלבנה שבצד אחד של פאה נתונה רוצה שפאה זו תנוע לכיוון אחד, ואילו הלבנה שבצידהּ השני של אותה הפאה רוצה שהפאה תנוע בכיוון ההפוך. תסכול במטא-קובייה גורם לה להיות קשיחה יותר בהשוואה למטא-קובייה לא מתוסכלת, או תואמת, כיוון שיש להפעיל כוח רב יותר כדי להתגבר על התסכול ולעוות את המטא-חומר.
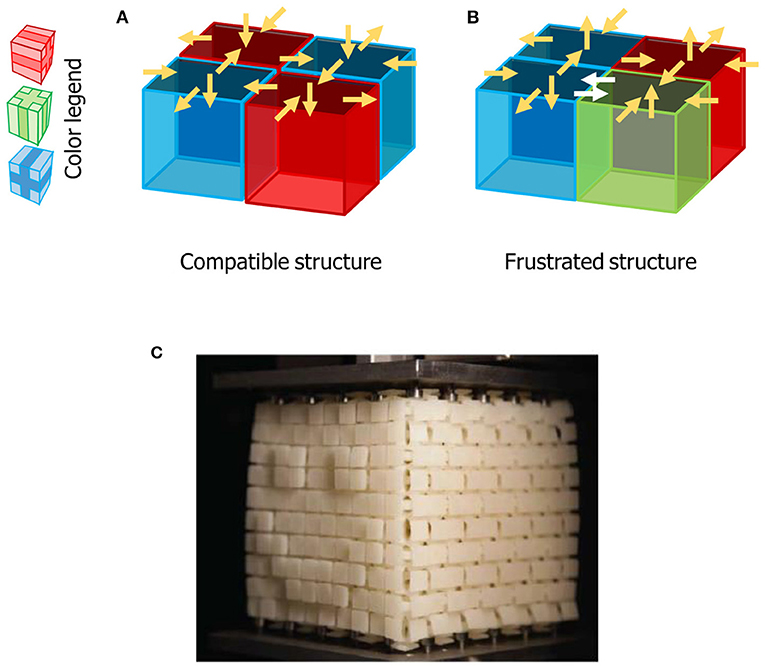
- איור 3 - מצבים אפשריים של מטא-קובייה.
- A. כאשר תאי היחידה מאורגנים במבנה תואם, ניתן לְרַצּוֹת את כולם בו בזמן, ונוצר מבנה אשר קל לדחוס אותו. ניתן לראות זאת באיור על ידי החיצים הצהובים, המצביעים על כיוון העיוות של כל פאה. B. אם תאי היחידה מאורגנים כך שלא ניתן לְרַצּוֹת את כולם בו זמנית לפחות פאה אחת במבנה תהיה מתוסכלת. מצב זה מוצג באיור על ידי החיצים הלבנים הכפולים, המדגימים תחרות בין שני כיוונים מנוגדים של העיוות. עקב כך החומר יהיה קשיח יותר. צבעי הקוביות מצביעים על הכיוון שבו כל תא יחידה ממוקם. C. עיצבנו מטא-קובייה שתתעוות לצורה רצויה (פרצוף מחייך)1, כאשר מפעילים עליה לחץ (האיור אומץ מ-Coulais ושותפים [3]).
מטא-חומרים מתאימים: כשלוחצים במקומות הנכונים
בשביל לנתח את כל המטא-קוביות האפשריות, לרבות אלה המורכבות מהרבה יותר מארבע לבנים, בָּנִינוּ מודל מתמטי, המאפשר לנו לדעת אם מטא-קובייה נתונה היא מתוסכלת או תואמת. המודל שפיתחנו איפשר לנו לזהות את כל המטא-קוביות התואמות, כלומר כאלו שיכולות להתעוות ללא תסכול באף אחד מתאי היחידה שבתוכן. באמצעות המודל הזה גילינו כי מספר המטא-קוביות התואמות הוא עצוּם! גדול כל כך, שביכולתנו לְעַצֵּב מטא-קובייה שבה יתקבל על פאה אחת שלה כל דפוס עיוות שבו נחפוץ. לדוגמה, עיצבנו את המטא-קובייה המופיעה באיור 3C כך שכאשר נלחץ עליה מלמעלה ומלמטה, היא תתעוות עם בליטות ושקעים שייצרו פרצוף מחייך על חזיתה1. אם נלחץ על החזית שלה עם אותו דפוס מסוים של פרצוף מחייך, המטא-קובייה תתעוות יחסית בקלות. לעומת זאת אם נלחץ עליה עם דפוס אחר, כמו דפוס שטוח לדוגמה, יהיה קשה יותר לעוות מטא-חומר זה. המודל המתמטי שפיתחנו מאפשר לנו לנבא כיצד קשיחוּת המטא-קובייה תִּגדל כתלות בתסכול שנייצר על ידי דפוס הלחיצה בו נשתמש. במילים אחרות, הראינו כי היכולת לעוות מטא-חומר תלויה לא רק בכוח שאנו מפעילים עליו או בסוג הגומי שממנו המטא-קובייה יוצרה, אלא במידה רבה גם בתאימוּת שבין התבנית שעימה אנו לוחצים לבין המבנה הייחודי של אותה מטא-קובייה.
שימושים אפשריים במטא-חומרים
המטא-קוביות שפיתחנו הן מערכת מעניינת, שבאמצעותה ניתן לחקור תאימוּת ותסכול המתרחשים בחומר. כאשר אנו משלבים ’לבנים‘ זהוֹת בעלות דפוס חוזר המונָּחות בכיוונים שונים, כדי ליצור מטא-קוביות גדולות, אנו יכולים לתכנן חומרים שכל אחד מהם מתעוות באופן מסוים כאשר מופעל עליו לחץ. היכולת לשלוט על הצורה שבה החומר מתעוות, עשויה להיות שימושית למגוון סוגי טכנולוגיות. למשל, תָּאֲרוּ לכם רובוט שיוכל לכוונן את קשיחוּת הזרוע שלו כדי לתפוס דברים ביעילוּת רבה יותר. לחלופין, מטא-חומרים יוכלו לְשַׁמֵּשׁ ליצירת שתלים רפואיים, או רגליים תותבות המותאמים בדיוק לגוף שאליו הם מוכנסים או מחוברים. השימוש במטא-חומרים עשוי גם להפחית את השימוש שאנו עושים במשאבי הטבע היקרים של כדור הארץ. כעת תוכלו להיווכח כי מטא-חומרים אינם רק חומרים מעניינים שיכולים ללמדנו על תסכול; הם עשויים גם לעזור לנו לשפר חיים של אנשים, ולסייע בשמירה על כדור הארץ!
מימון
מחקר זה מומן באופן חלקי על ידי הקרן הלאומית למדע של ישראל, ועל ידי הארגון למחקר מדעי בהולנד.
מילון מונחים
תסכול (Frustration): ↑ חוסר היכולת למלא בו זמנית כמה דרישות סותרות. [https://en.wikipedia.org/wiki/Geometrical_frustration].
גביש (Crystal): ↑ חומר מוצק שמרכיביו מאורגנים בצורה מסודרת. [https://en.wikipedia.org/wiki/Crystal].
סריג (Lattice): ↑ מבנה חזרָתי ששומר על מראהו גם לאחַר שמזיזים אותו בכיוונים שונים. [https://en.wikipedia.org/wiki/Bravais_lattice].
אטום (Atom): ↑ היחידה הקטנה ביותר של חומר רגיל שממנו עשוי יסוד כימי. [https://en.wikipedia.org/wiki/Atom].
מטא-חומר (Meta-material): ↑ חומר מלאכותי אשר תכונותיו תלויות בעיקר במבנה המהונדס של הַתָּאים המרכיבים אותו. [https://en.wikipedia.org/wiki/Metamaterial].
תא יחידה (Unit cell): ↑ דפוס שחוזר על עצמו ומרכיב חומר גבישי. [https://en.wikipedia.org/wiki/Unit_cell].
מטא-קובייה (Meta-cube): ↑ מטא-חומר הבנוי מ’לבנים‘ בצורת קוביות, שחוזרות על עצמן, ומונחות בכיוונים שונים.
הצהרת ניגוד אינטרסים
המחברים מצהירים כי המחקר נערך בהעדר כל קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.
תודות
המחבּר מודה ליערה שוֹקֶף ולחביבה סִירוֹטָה על הערותיהן והצעותיהן המועילות בתהליך כתיבת מאמר זה והצגתו.
הערת שוליים
1. ↑ראו בסרטון זה – תכנון קומבינטורי של מטא-חומרים מכניים מורכבים.
מאמר המקור
↑Coulais, C., Teomy, E., de Reus, F., Shokef, Y., and van Hecke, M. 2016. Combinatorial design of textured mechanical metamaterials. Nature. 535:529–532. doi: 10.1038/nature18960
מקורות
[1] ↑ Wannier, G. H. 1950. Antiferromagnetism: the triangular Ising net. Phys. Rev. 79:357–364. doi: 10.1103/PhysRev.79.357
[2] ↑ Han, Y., Shokef, Y., Alsayed, A. M., Yunker, P., Lubensky, T. C., and Yodh, A. G. 2008. Geometric frustration in buckled colloidal monolayers. Nature. 456:898–903. doi: 10.1038/nature07595
[3] ↑ Coulais, C., Teomy, E., de Reus, F., Shokef, Y., and van Hecke, M. 2016. Combinatorial design of textured mechanical metamaterials. Nature. 535:529–532. doi: 10.1038/nature18960
