Abstract
Water flows through forests in many ways, so it is difficult to understand and predict where and when it will flow. Understanding how water flows through forests is important, as it affects many of the services that forests offer to people, like lumber for houses and cleaner air. Water scientists (called hydrologists) have a way to reduce the complex water flow of a forest into something we can explain with simple math: they turn forests into buckets! In this article, we describe a forest “water park,” where leafy and bark buckets fill and empty into each other or onto the forest floor. These buckets help us describe and predict water flows in forests using simple arithmetic and statistics. We focus on the flow of rainwater as it drains through the canopy to the ground, contributing water needed for tree growth and filling the groundwater that we drink.
Water Scientists and Their Love of Buckets
Water is an important part of nature, our societies, and our individual lives. It is cycling all the time—from land to the clouds; returning as precipitation; filling rivers, lakes, and seas; recharging groundwater aquifers; forming surface runoff; wetting fields and forests; and watering plants and trees. This movement of water is called the water cycle and it is studied by scientists called hydrologists. Hydrologists observe the various water processes in nature, trying to understand and predict them. Some water flows are hard to follow—for example, it is hard to watch liquid water become an invisible gas through evaporation. This makes the water cycle difficult to understand and even more difficult to explain or predict. To think about these complex processes, hydrologists imagine that all these processes act as one big water park full of interconnected buckets. Some buckets are being filled with rainfall, others with snow, and some are already full of water, which starts to overflow.
This mental “model” of nature may sound crazy, but it is actually quite useful in helping us understand and manage water. How? Well, let us begin by admitting something obvious: nature is very complex, so it can be hard to understand and predict. Even when we focus on one important piece of the water cycle—like, “how does rain recharge the soil in a forest?”—a lot of complexity remains [1]. For example, to reach the soil, rainwater must pass through the forest’s canopy, which has leaves and branches that stick out in all directions and angles (Figure 1A). At any point during a storm, rainwater could be stuck or moving or splashing anywhere throughout that forest canopy! How can we keep track of all the water—at all times during the storm and at all places in the canopy—to understand how much rain reaches the soil (Figure 1B)? We cannot, at least not without enormous expense and difficulty. But hydrologists using the “water park” approach investigate this complex process using a scientific technique called reductionism, which is a way to describe something complex in a simple way. All those branches and leaves can be thought of as buckets (Figure 1C)! No matter where the rainwater is sitting in the forest’s canopy, it is now simply sitting in a bucket. When a canopy bucket fills up, the extra rainwater empties out onto the soil below. Another benefit of this reduction (turning a canopy into a bucket) is that we can now use math to describe the evaporation (E) process, called rainfall interception, with some simple arithmetic:
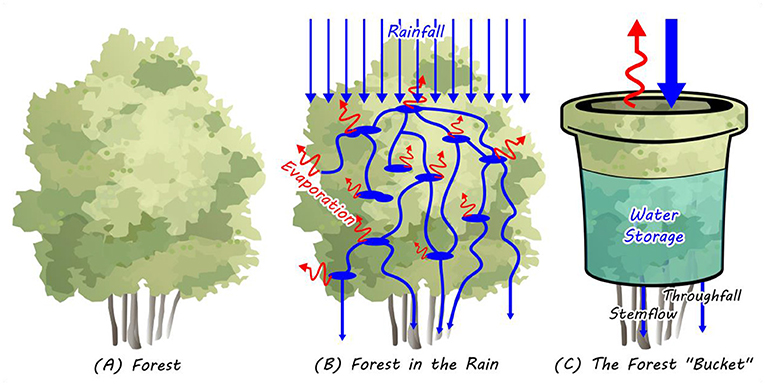
- Figure 1 - (A) A complex forest canopy.
- (B) In real life, the flow of rainwater through the canopy to the ground is a messy process. Blue arrows show rainfall and red arrows are evaporation. (C) Using reductionism, hydrologists can create a simple bucket model to make water flow in the forest easier to understand. This allows us to use simple math to describe the process of rainfall interception as the filling and emptying of the bucket.
In this equation, evaporation from rainfall interception (E) is really hard to measure (in fact, hydrologists still have not figured out how to measure this consistently [2]), but each of the letters on the right side of the equation represent something we can measure directly. If we measure the rain (R) falling in an open area next to trees, the rain that drips to the ground beneath the trees as throughfall (RT), and the rain that drains down the tree trunks as stemflow (RS), then we can estimate E.
Poking Holes in Hydrologists’ Buckets
Most of a hydrologists’ buckets have a big hole at the top, so that storms can fill the buckets and evaporation can empty them. This is the case for a canopy bucket—the rain fills it up, while some water is constantly evaporating back into the atmosphere. But, to make the canopy bucket reduction more useful, we must poke two holes in it: one for throughfall and another for stemflow. These holes need to change based on how much water enters the canopy bucket over time. And all canopy buckets are not the same because there are many different kinds of trees.
Let us say that the bucket model is being used by hydrologists to understand and predict stemflow. The amount and timing of stemflow mostly depend on how much water the tree bucket can hold, how well the tree can drain rainwater to the trunk, and how the storm delivers the rainfall. All three of these categories are described by what are called variables, describing characteristics or values that can be measured or counted. For example, some trees have flat leaves, others have needles, and the leaves of some trees fall off during the winter. Trees can have a lot of trunks and branches or only one main trunk, and some trees have smooth bark while the others have thick, rough bark. All of these are different variables/tree properties that determine the size of the bucket and how well the canopy will drain rainwater to that bucket (Figure 2). That is a lot of properties, so let us reduce them all to a single number that will adjust the rainfall amount by the portion of rainfall that is captured by the canopy and drained to the trunk. Hydrologists call this the trunk drainage coefficient (pt), and it can range from 0 to 100%! Thus, the bucket that overflows to make stemflow only receives the rainfall (R) times this coefficient, and minus the evaporation. Since the amount of water in the bucket (C) can sometimes be less than the total capacity of the bucket (S), we can adjust the evaporation rate [3]. Using math, we can write it like this:
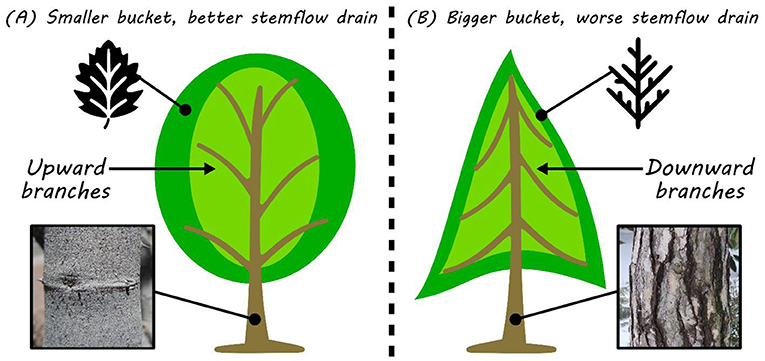
- Figure 2 - Different types of trees have different canopy properties that affect the flow of rainwater to the ground.
- (A) This tree has a smaller water storage bucket that drains greater amounts of rainwater to the trunk, compared to the tree in (B), which has a larger water storage bucket that poorly drains rainwater to the trunk.
To estimate the evaporation rate, we need also information about the weather. Water will run down the trunk differently during a short, intense summer rainstorm, a long winter rainstorm, or a gentle spring drizzle. It is as if different holes are poked in the bucket depending on how much rain falls during the storm, how long it falls for, how much wind is blowing, whether it is warm or cold, and whether raindrops are large, small, numerous, or scattered. So, what is a useful way to deal with all these interacting conditions?
Statistics: Crafting Buckets for all Weather and Trees
If we are not careful, all of these interacting forest and weather variables can turn our simple bucket water park back into a complex mess. Then, the equations we described above will seem too simple to be useful. But this does not happen because hydrologists pair these reductions with other mathematical methods, called statistics. This field of math helps us to make sense of large amounts of data, including its collection, organization, and analysis.
For example, hydrologists will often look to see if stemflow from a certain tree has a relationship with one weather variable, like the amount of rainfall. This relationship, called a correlation, can help us calculate the size of the bucket, how well the canopy drains rainwater to the trunk, and even how much evaporation occurs on the bark! Figure 3A shows an example tree that required 10 mm of rainfall to fill the canopy bucket and to get the bark wet enough to start stemflow flowing. Once stemflow began, the tree canopy could drain 1 mm of every additional 10 mm of rain to the trunk as stemflow. So, we now have the bucket size (10 mm) and the stem drainage coefficient (1/10 = 10%) for this tree!
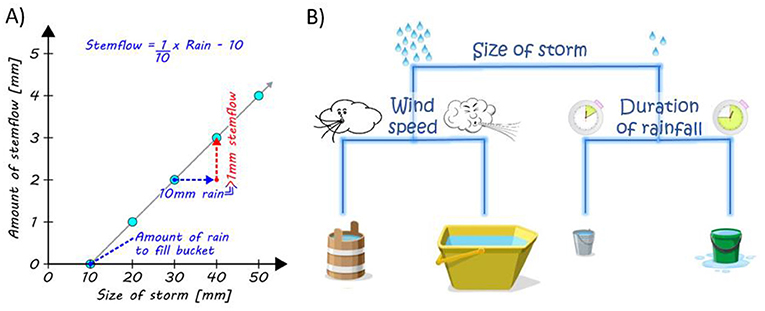
- Figure 3 - Statistical analysis of stemflow data for an example tree.
- (A) A simple correlation plot between rainfall and stemflow that shows how a bucket can be sized (the lowest point on the horizontal axis) and the drainage coefficient estimated (blue and red arrows). (B) A simplification of a more complex statistical method, showing consideration of more variables in determining the most appropriate type of bucket [4]. Using more observations of stemflow across more types of storms, we can discover what types of buckets would be better for windy or calm conditions or for storms of different durations (longer or shorter).
This example uses only two variables, but we can look for correlations between stemflow and all the tree and weather variables at the same time, using more complex statistical methods. For example, hydrologists can use statistics to represent a tree canopy as different types of buckets according to different weather conditions (Figure 3B). In this way, hydrologists can still use the bucket concept even if the tree canopy responds differently in big windy storms compared to small windless storms. Using these methods, hydrologists can not only poke the right kinds of holes in the bucket, but they can also understand why some holes should be larger or why they should be positioned differently. These methods transform the messy reality of nature into the neat and orderly bucket water park.
The Importance of Hydrologists’ Buckets
Water is needed for all life on Earth, so it is no wonder that there is water all over our planet—including inside the Earth and inside us! It is therefore difficult to know where water is, how it moves around, and when it is where. Still, it is important to follow, understand, and predict the water cycle and how human actions will influence it. To reduce this complex water cycle into something we humans can follow, understand, and predict, the reductionist bucket approach is very useful. In this article, we focused on one type of bucket (the forest canopy) and one type of water flow that occurs during storms in the forest (stemflow). The forest bucket and its water flows are extremely important to understand because forests provide many services to humanity—from producing lumber used to build houses to cooling the air. Many of these services depend on the way water flows through the forest “water park.” By reducing the complexity of the forest water cycle, hydrologists can describe those complex processes using math, which you now know is simple enough to be learned by kids all over the world!
Glossary
Hydrologist: ↑ Scientist, who studies water and its movement around the planet.
Evaporation: ↑ A major process in the water cycle that happens when liquid water turns into a gas.
Reductionism: ↑ Analyzing and describing a complex process in a simple way, so that humans can better understand a process and make predictions.
Rainfall Interception: ↑ The part of rain (or snow) that does not make it to the ground beneath plants, because some of it evaporates while passing through plants’ leaves and branches.
Throughfall: ↑ Rainwater that falls through gaps in the forest and that drips from leaves and branches to the ground.
Stemflow: ↑ Rainwater that drains down the tree trunk to the forest floor.
Variables: ↑ Characteristics, number, or quantity that can be measured or counted.
Trunk Drainage Coefficient: ↑ The portion of rainfall that is captured by the canopy and drained to the trunk.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The paper was prepared as part of the activities at the UNESCO Chair of Water-related Disaster Risk Reduction, University of Ljubljana, Slovenia.
References
[1] ↑ Allen, S. T., Aubrey, D. P., Bader, M. Y., Coenders-Gerrits, M., Friesen, J., Gutmann, E. D., et al. 2020. “Key questions on the evaporation and transport of intercepted precipitation,” in Precipitation Partitioning by Vegetation (Cham: Springer). p. 269–80.
[2] ↑ Coenders-Gerrits, M., Schilperoort, B., and Jiménez-Rodríguez, C. 2020. “Evaporative processes on vegetation: an inside look,” in Precipitation Partitioning by Vegetation (Cham: Springer). p. 35–48.
[3] ↑ Rutter, A. J., Kershaw, K. A., Robins, P. C., and Morton, A. J. 1971. A predictive model of rainfall interception in forests, 1. Derivation of the model from observations in a plantation of Corsican pine. Agric. Meteorol. 9:367–84. doi: 10.1016/0002-1571(71)90034-3
[4] ↑ Bezak, N., Zabret, K., and Šraj, M. 2018. Application of copula functions for rainfall interception modelling. Water. 10:995. doi: 10.3390/w10080995
