Abstract
From a young age, we are told that being “in sync” is a good thing! From being in sync with the music as we dance to being in sync with teammates on the field, synchronization is celebrated. However, too little or too much synchronization can be bad. In the brain, synchronization allows important information to be sent back and forth between neurons, so that we can make decisions and function in our daily lives. Mathematics can help researchers and doctors understand patterns of abnormal synchronization in the brain and help them to diagnose and potentially treat the symptoms of brain disorders. In this article, we will dive into how mathematics is used to explore and understand the brain—one of our body’s most important organs.
What Is Synchronization in the Brain and Why Does It Happen?
Synchronization is a way that some parts of the brain send valuable information to other parts. Neurons (nerve cells) in the brain are the cells that transmit this information, both to other brain neurons and to the body. As humans, we take in so much information! We are constantly smelling, seeing, hearing, and observing things in the world around us, and we are also constantly creating thoughts and actions from all of this information. Hundreds of these interactions can happen each second, and this can sometimes be overwhelming. Have you ever noticed it is hard to talk and listen at a crowded, noisy party? With so much background noise, you might feel like you need to shout for others to hear you! The human brain has the same struggle when communicating with other parts of the brain or the body. This is where synchronization of neurons is important. Synchronization means two processes show coordinated rhythmic activity (like peaking at the same time). As messenger cells that communicate and relay information, neurons can synchronize with each other to communicate better.
Take a look at Figure 1. When the two children are in sync together on the swings, they can easily hear each other and talk. But when they are not in sync, it is much harder to communicate. All the background noise and the distance between them make it harder to hear what the other is trying to say. Synchronization in the brain is just as important: it allows neurons to communicate effectively, so that important information can be sent where it needs to go! Synchronization means that different neurons generate bouts of electrical activity at the same time, which facilitates the exchange of information between neurons. Specific areas of the brain are responsible for various activities such as speech, movement, vision, and hearing. It is vital that synchronization occurs, to allow all of these brain areas to communicate with each other, so that our minds and our bodies can function properly.

- Figure 1 - (A) When the two children swing in sync with each other, they can easily communicate.
- (B) When the children are not in sync, it is more difficult to communicate. Something similar happens in the brain. When neurons are in sync, they are able to transmit important information to each other (image credit: Subrina Pumford, subrinapumford.com).
Imagine a third child, not pictured in the figure above, swinging next to the two children in the figure. If the two children were constantly in sync and talking with each other, it would be hard for the third child, who isn’t in sync, to talk with them. The two in-sync children would not be able to hear other voices very well. Scientists have discovered that if brain neurons are too in sync, this can actually be harmful, because new information is not able to be transmitted through neurons that are too consumed by “talking” to each other. This can cause the loss of activities such as speech and movement. People with brain disorders such as Parkinson’s disease may have excessive synchronization of brain neurons. It seems like the brain needs to be in sync a little bit, but not too much! Being in sync the right amount may allow neurons to communicate, but if neurons are in sync too much with each other, these neurons will have difficulty in responding to new information. Thus, one part of the brain will not be able to appropriately respond to signals from another part of the brain and will not be able to, for example, properly make some movements as is happening in patients with Parkinson’s disease. How can researchers and scientists figure out how much communication is needed?
Scientists and Mathematicians Working Together
While scientists work hard to gather data, mathematicians are needed to make sense of all the information collected. Scientists can use techniques like electroencephalography (EEG) to record and analyze the brain’s electrical activity. Mathematicians can analyze the data to find out whether there is synchrony or not.
The average amount of synchrony present in the brain is important, but the patterns of synchrony over time are important, too [1, 2]. Look at Figure 2. Although the averages for all the curves are identical, the patterns are actually quite different.
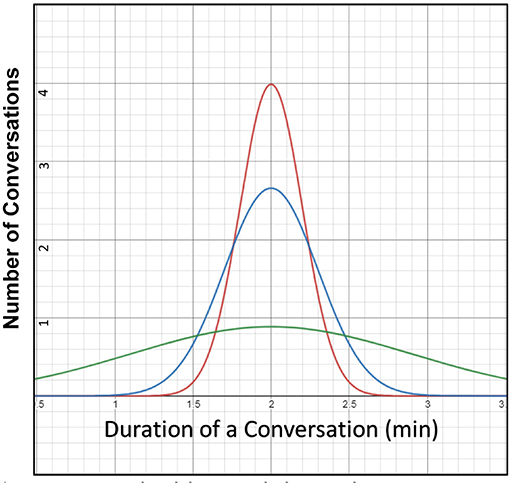
- Figure 2 - All three curves in this graph have the same center and the same average duration of a conversation of 2 min, but the curves are very different in shape! The same average duration of a conversation does not mean that the shape and pattern of the data are also the same.
- In terms of synchrony in the brain, this means different types of brain activity may seem the same when looking at one type of measure, like the average, yet their pattern is much different.
Here is an example of how two different patterns of data, with the same average, can affect how much information is being exchanged. Find a friend or family member to talk with for 1 min. While talking, cover your ears for half a second, and then uncover your ears for half a second. Repeat this process until your 1 min is up! Now, talk for another minute, but this time, cover your ears for 30 s and then uncover them for 30 s. For both minutes, you spent 30 s covering your ears and 30 talking with uncovered ears. But which time could you understand more? Chances are you probably had an easier time understanding the conversation during the half-second intervals of covering your ears. In the other minute, you completely missed the first part of the conversation.
It is important to note that different temporal patterns of synchronization in the brain may also have the same averages but tell very different stories [1–3]. As two brain parts are engaged in rare but long episodes of synchrony, they will not be able to respond to commands from other brain parts during synchronized episodes and important information will be lost. If these same two parts are involved in many short synchronous episodes, other brain parts will be able to communicate through frequent periods of no synch.
Mathematics at Work
After doctors or researchers collect EEG data, those data must be transformed by mathematicians so that patterns and cycles can be observed. This process helps the researchers to make sense of the data. How can data be broken down so that researchers can understand it? A technique called Fourier analysis allows mathematicians to break down complex signals into many simple waveforms and to sort out fast and slow waves (Figure 3A). By doing so, we can take complicated and noisy brain activity data and focus on the parts researchers are interested in. The data look much smoother after the appropriate waves are isolated from the complicated experimental data, which helps scientists draw conclusions about synchronization in the brain. Of course, as we isolate some nice waves from the experimental data, we are unavoidably leaving some information out, but the key is to remove mostly the non-essential information to highlight the most important information.
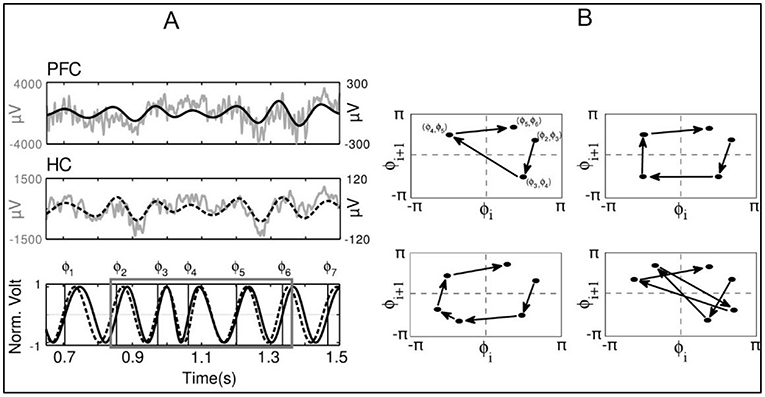
- Figure 3 - (A) Has the real brain EEG data and processed oscillations resulting from Fourier analysis.
- (B) Presents the phase maps, where one may study the chain of transitions (shown as arrows) with different mathematical tools. The real data are messy.
Phase maps are another mathematical tool that can give scientists insight into synchronization and desynchronization cycles and how long those cycles last (Figure 3B). Desynchronization cycles are the moments when neurons are not in sync with one another. Phase maps check what happens with one oscillation while another oscillation is, for example, at a peak. Synchronization of oscillations is when oscillations are peaking at the same time, or one peaks with a fixed delay after another. Phase maps allow researchers to visualize neuron synchronization and desynchronization to answer important scientific questions.
Other mathematical equations are used to help scientists understand how one part of the brain communicates, behaves, and interacts with other parts of the brain. One type of mathematics used for this purpose is called differential equations. Differential equations are mathematical descriptions of how something changes over time. Mathematicians and physicists have used differential equations for several centuries and now they are used in brain science too! Differential equations describe very complicated interactions between neurons and can help researchers to understand very complex brain activity.
Analysis of brain data using differential equations has shown us that short periods of desynchronization make it easier for some brain parts to respond to signals from other brain parts [4, 5] (recall the example of covering your ears). Without shorts periods of desynchronization, or time when neurons are not in sync, neurons cannot take in all the valuable information that they need!
Conclusion
Different patterns of neuron activity may have the same average amount of synchronization. Unique patterns of synchronization are associated with several different brain disorders, such as Parkinson’s disease, addiction, and autism spectrum disorder. What appears to be a common theme is that temporal patterning of neural synchronization may be fine-tuned in a healthy brain. Different brain disorders may disrupt this patterning in different ways, but in all of them it may negatively affect communication between brain parts. This, in turn, results in very debilitating symptoms. These brain disorders can cause serious harm, so researchers should understand as much as possible about them, to help those who suffer from these disorders.
There is still much research to be done to understand synchronization and the role it plays in the brain, in both health and disease. Mathematics is a powerful tool that help with this exploration, allowing doctors and scientists to learn more the functioning of our most complex organ!
Funding
This study was supported by NSF DMS 1813819.
Glossary
Synchronization: ↑ A state in which two or more processes (frequently, two or more oscillations) are coordinated in time, such as peaking at the same time.
Neuron: ↑ Nerve cells, including nerve cells in the brain, that send and receive electrical messages with other cells. We use neurons to sense, to feel, to think, and to control our actions.
Electroencephalography (EEG): ↑ A technique for measuring electrical activity in the brain by using electrodes (small discs) attached on the head. This technique does not get inside of the brain, and is thus not harmful.
Fourier Analysis: ↑ An area of mathematics and of data analysis, that studies the properties of oscillations. It represents complex waveforms in terms of many simple waveforms, which may substantially simplify analysis of the data.
Phase Maps: ↑ Mathematical technique that simplifies the analysis of oscillatory signals. Roughly speaking, it lets to look at how the time of the peak of oscillations depends on the timing of the previous peaks.
Desynchronization Cycles: ↑ Intervals of time when neurons are not in sync with one another.
Oscillation: ↑ A wave-like behavior of some quantity, oscillating quantity goes up and down with more or less regular frequency (as opposed to, for example, saturation or completely random behavior). Electrical activity of the brain discussed here frequently shows oscillations, see Figure 3A for the wave-like patterns of brain activity.
Differential Equations: ↑ Mathematical equations that describe how something changes over time.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Original Source Article
↑Ahn, S., and Rubchinsky, L. L. 2017. Potential mechanisms and functions of intermittent neural synchronization. Front. Comput. Neurosci. 11:44. doi: 10.3389/fncom.2017.00044
References
[1] ↑ Ahn, S., Rubchinsky, L. L., and Lapish, C. C. 2014. Dynamical reorganization of synchronous activity patterns in prefrontal cortex—hippocampus networks during behavioral sensitization. Cereb. Cortex 24:2553–61. doi: 10.1093/cercor/bht110
[2] ↑ Ahn, S., Zauber, S. E., Worth, R. M., Witt, T., and Rubchinsky, L. L. 2018. Neural synchronization: average strength vs. temporal patterning. Clin. Neurophysiol. 129:842–4. doi: 10.1016/j.clinph.2018.01.063
[3] ↑ Malaia, E., Ahn, S., and Rubchinsky, L. L. 2020. Dysregulation of temporal dynamics of synchronous neural activity in adolescents on autism spectrum. Autism Res. 13:24–31. doi: 10.1002/aur.2219
[4] ↑ Ahn, S., and Rubchinsky, L. L. 2013. Short desynchronization episodes prevail in synchronous dynamics of human brain rhythms. Chaos 23:013138. doi: 10.1063/1.4794793
[5] ↑ Ahn, S., and Rubchinsky, L. L. 2017. Potential mechanisms and functions of intermittent neural synchronization. Front. Comput. Neurosci. 11:44. doi: 10.3389/fncom.2017.00044
