Abstract
Prime numbers have attracted human attention from the early days of civilization. We explain what they are, why their study excites mathematicians and amateurs alike, and on the way we open a window to the mathematician’s world.
From the beginning of human history, prime numbers aroused human curiosity. What are they? Why are the questions related to them so hard? One of the most interesting things about prime numbers is their distribution among the natural numbers. On a small scale, the appearance of prime numbers seems random, but on a large scale there appears to be a pattern, which is still not fully understood. In this short paper, we will try to follow the history of prime numbers since ancient times and use this opportunity to dive into and better understand the mathematician’s world.
Composite Numbers and Prime Numbers
Have you ever wondered why the day is divided into exactly 24 h, and the circle into 360 degrees? The number 24 has an interesting property: it can be divided into whole equal parts in a relatively large number of ways. For example, 24÷2 = 12, 24÷3 = 8, 24÷4 = 6, and so on (complete the rest of the options yourself!). This means that a day can be divided into two equal parts of 12 h each, daytime and nighttime. In a factory that works non-stop in 8-h shifts, each day is divided into exactly three shifts.
This is also the reason why the circle was divided into 360°. If the circle is divided into two, three, four, ten, twelve, or thirty equal parts, each part will contain a whole number of degrees; and there are additional ways of dividing a circle that we did not mention. In ancient times, dividing a circle into equal-sized sectors with high precision was necessary for various artistic, astronomical, and engineering purposes. With a compass and protractor as the only available instruments, division of a circle into equal sectors had great practical value.1
A whole number that can be written as the product of two smaller numbers is called a composite number. For example, the equations 24 = 4 × 6 and 33 = 3 × 11 show that 24 and 33 are composite numbers. A number that cannot be broken down in this way is called a prime number. The numbers
2, 3, 5, 7, 11, 13, 17, 19, 23, and 29
are all prime numbers. In fact, these are the first 10 prime numbers (you can check this yourself, if you wish!).
Looking at this short list of prime numbers can already reveal a few interesting observations. First, except for the number 2, all prime numbers are odd, since an even number is divisible by 2, which makes it composite. So, the distance between any two prime numbers in a row (called successive prime numbers) is at least 2. In our list, we find successive prime numbers whose difference is exactly 2 (such as the pairs 3,5 and 17,19). There are also larger gaps between successive prime numbers, like the six-number gap between 23 and 29; each of the numbers 24, 25, 26, 27, and 28 is a composite number. Another interesting observation is that in each of the first and second groups of 10 numbers (meaning between 1–10 and 11–20) there are four prime numbers, but in the third group of 10 (21–30) there are only two. What does this mean? Do prime numbers become rarer as the numbers grow? Can anyone promise us that we will be able to keep finding more and more prime numbers indefinitely?
If, at this stage, something excites you and you wish to keep investigating the list of prime numbers and the questions we raised, this means that you have a mathematician’s soul. Stop! Do not continue reading!2 Grab a pencil and a piece of paper. Write all the numbers up to 100 and mark the prime numbers. Check how many pairs with a difference of two are there. Check how many prime numbers there are in each group of 10. Can you find any patterns? Or does the list of prime numbers up to 100 seem random to you?
Some History and the Concept of a Theorem
Prime numbers have occupied human attention since ancient times and were even associated with the supernatural. Even today, in modern times, there are people trying to provide prime numbers with mystical properties. The well-known astronomer and science author Carl Sagan wrote a book in 1985 called “Contact,” dealing with extraterrestrials (a human-like culture outside of earth) trying to communicate with humans using prime numbers as signals. The idea that signals based on prime numbers could serve as a basis for communication with extraterrestrial cultures continues to ignite the imagination of many people to this day.
It is commonly assumed that serious interest in prime numbers started in the days of Pythagoras. Pythagoras was an ancient Greek mathematician. His students, the Pythagoreans—partly scientists and partly mystics—lived in the sixth century BC. They did not leave written evidence and what we know about them comes from stories that were passed down orally. Three hundred years later, in the third century BC, Alexandria (in modern Egypt) was the cultural capital of the Greek world. Euclid (Figure 1), who lived in Alexandria in the days of Ptolemy the first, may be known to you from Euclidean geometry, which is named after him. Euclidean geometry has been taught in schools for more than 2,000 years. But Euclid was also interested in numbers. In the ninth book of his work “Elements,” in Proposition 20, there appears for the first time a mathematical proof of the theorem that there are infinitely many prime numbers.

- Figure 1
- The people behind the prime numbers.
This is a good place to say a few words about the concepts of theorem and mathematical proof. A theorem is a statement that is expressed in a mathematical language and can be said with certainty to be either valid or invalid. For example, the theorem “there are infinitely many prime numbers” claims that within the system of natural numbers (1,2,3…) the list of prime numbers is endless. To be more precise, this theorem claims that if we write a finite list of prime numbers, we will always be able to find another prime number that is not on the list. To prove this theorem, it is not enough to point out an additional prime number for a specific given list. For instance, if we point out 31 as a prime number outside the list of first 10 primes mentioned before, we will indeed show that that list did not include all prime numbers. But perhaps by adding 31 we have now found all of the prime numbers, and there are no more? What we need to do, and what Euclid did 2,300 years ago, is to present a convincing argument why, for any finite list, as long as it may be, we can find a prime number that is not included in it. In the next section, we will present Euclid’s proof, without burdening you with too much detail.
Euclid’s Proof for the Existence of Infinitely Many Prime Numbers
To prove that there are infinitely many prime numbers, Euclid used another basic theorem that was known to him, which is the statement that “every natural number can be written as a product of prime numbers.” It is easy to be convinced of the truth of this last claim. If you pick a number that is not composite, then that number is prime itself. Otherwise, you can write the number you chose as a product of two smaller numbers. If each of the smaller numbers is prime, you have expressed your number as a product of prime numbers. If not, write the smaller composite numbers as products of still smaller numbers, and so forth. In this process, you keep replacing any of the composite numbers with products of smaller numbers. Since it is impossible to do this forever, this process must end and all the smaller numbers you end up with can no longer be broken down, meaning they are prime numbers. As an example, let us break down the number 72 into its prime factors:
72 = 12 × 6 = 3 × 4 × 6 = 3 × 2 × 2 × 6 = 3 × 2 × 2 × 2 × 3.
Based on this basic fact, we can now explain Euclid’s beautiful proof for the infinitude of the set of prime numbers. We will demonstrate the idea using the list of the first 10 primes but notice that this same idea works for any finite list of prime numbers. Let us multiply all the numbers in the list and add one to the result. Let us give the name N to the number we get. (The value of N does not actually matter since the argument should be valid for any list.)
N = (2 × 3 × 5 × 7 × 11 × 13 × 17 × 19 × 23 × 29)+1.
The number N, just like any other natural number, can be written as a product of prime numbers. Who are these primes, the prime factors of N? We do not know, because we have not calculated them, but there is one thing we know for sure: they all divide N. But the number N leaves a remainder of one when divided by any of the prime numbers on our list 2, 3, 5, 7,…, 23, 29. This is supposed to be a complete list of our primes, but none of them divides N. So, the prime factors of N are not on that list and, in particular, there must be new prime numbers beyond 29.
The Sieve of Eratosthenes
Have you found all the prime numbers smaller than 100? Which method did you use? Did you check each number individually, to see if it is divisible by smaller numbers? If this is the way you chose, you definitely invested a lot of time. Eratosthenes (Figure 1), one of the greatest scholars of the Hellenistic period, lived a few decades after Euclid. He served as the chief librarian in the library of Alexandria, the first library in history and the biggest in the ancient world. He was interested not only in mathematics but also in astronomy, music, and geography, and was the first to calculate the earth’s circumference with an impressive precision for his time. Among other things, he designed a clever way to find all the prime numbers up to a given number. Since this method is based on the idea of sieving (sifting) the composite numbers, it is called the Sieve of Eratosthenes.
We will demonstrate the sieve of Eratosthenes on the list of prime numbers smaller than 100, which is hopefully still in front of you (Figure 2). Circle the number 2, since it is the first prime number, and then erase all its higher multiples, namely all the composite even numbers. Move on to the next non-erased number, the number 3. Since it was not erased, it is not a product of smaller numbers, and we can circle it knowing that it is prime. Again, erase all its higher multiples. Notice that some of them, such as 6, have been already deleted, while others, such as 9, will be erased now. The next non-erased number—5—will be circled. Again, erase all its higher multiples: 10, 15, and 20 have already been deleted, but 25 and 35, for instance, should be erased now. Continue in the same manner. Until when? Try to think why after passing we do not need to continue the process. All numbers smaller than 100 that were not erased are prime numbers and can be safely circled!
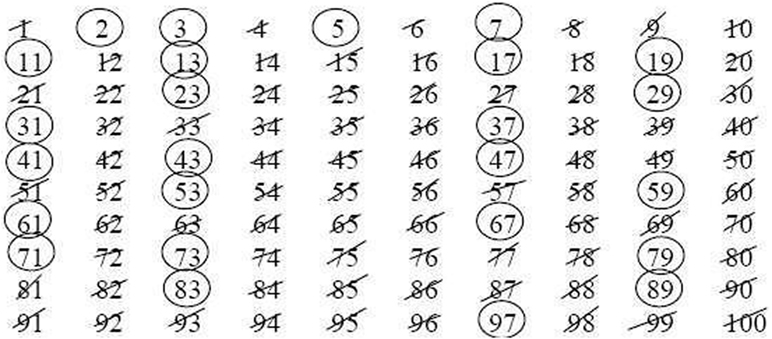
- Figure 2 - Sieve of Eratosthenes.
- Composite numbers are crossed out and prime numbers are circled.
Frequency of Prime Numbers
What is the frequency of prime numbers? How many prime numbers are there, approximately, between 1,000,000 and 1,001,000 (one million and one million plus one thousand) and how many between 1,000,000,000 and 1,000,001,000 (one billion and one billion plus one thousand)? Can we estimate the number of prime numbers between one trillion (1,000,000,000,000) and one trillion plus one thousand?
Calculations reveal that prime numbers become more and more rare as numbers get larger. But is it possible to state an accurate theorem that will express exactly how rare they are? Such a theorem was first stated as a conjecture by the great mathematician Carl Friedrich Gauss in 1793, at the age of 16. The nineteenth-century mathematician Bernhard Riemann (Figure 1), who influenced the study of prime numbers in modern times more than anyone else, developed further tools needed to deal with it. But a formal proof of the theorem was given only in 1896, a century after it had been stated. Surprisingly, two independent proofs were provided the same year by the French Jacques Hadamard and the Belgian de la Vallée-Poussin (Figure 1). It is interesting to note that both men were born around the time of the death of Riemann. The theorem they proved received the name “the prime number theorem” due to its importance.
The precise formulation of the prime number theorem, even more so the details of its proof, require advanced mathematics that we cannot discuss here. But put less precisely, the prime number theorem states that the frequency of prime numbers around x is inversely proportional to the number of digits in x. In the above example, the number of primes in a “window” of length 1,000 around one million (by which we mean the interval between one million and one million and one thousand) will be 50% larger than the number of primes in the same “window” around one billion (the ratio is 9:6, just like the ratio between the number of zeroes in one billion and one million), and about twice as much as the number of primes in the same window around one trillion (where the ratio of the number of zeroes is 12:6). Indeed, computer calculations show that there are 75 prime numbers in the first window, 49 in the second and only 37 in the third, between one trillion and one trillion plus one thousand.
The same information can be pictured as a graph, shown below (Figure 3). You can see how the number π(x) of primes up to x changes in the range x ≤ 100, and again for x ≤ 1,000. Notice that any time we meet a new prime along the x-axis, the graph rises by 1, so the graph takes the shape of steps (Figure 3A). On a small scale, it is hard to detect a pattern in the graph. It is quite easy to prove that we can find arbitrarily large intervals in which there are no prime numbers, meaning spans where the graph does not rise. On the other hand, a famous conjecture (see below) states that there are infinitely many twin primes, that is, pairs of primes with a difference of 2 between them, which would translate to a “step” of width 2 in the graph. On a larger scale, however, the graph looks smooth (Figure 3B). This smooth curve seen on a large scale demonstrates the prime number theorem.
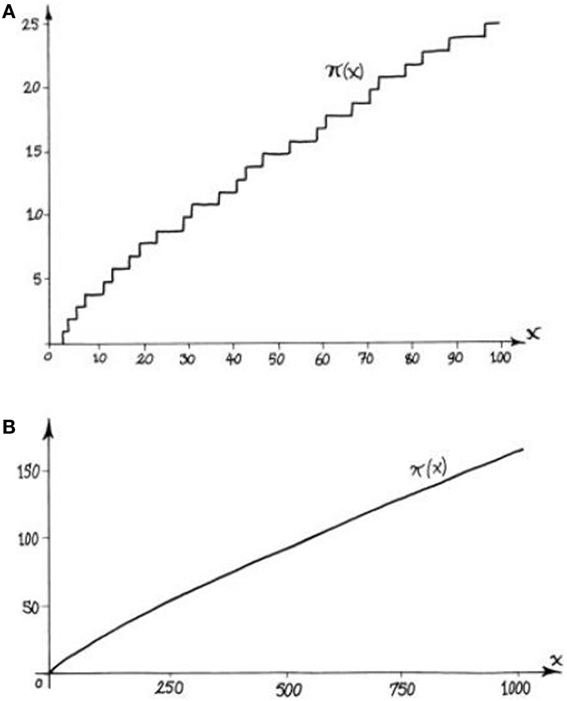
- Figure 3 - Frequency of the prime numbers.
- Graphs showing π(x), the number of primes up to the number x. In panel A. x ranges from 0 to 100, and the graph is step-like. In panel B. x ranges from 0 to 1,000, so the scale is larger and the graph appears to be much smoother.
The fact that a mathematical phenomenon seems to behave randomly in one scale but shows regularity (smoothness) in a different/larger scale—a regularity which becomes more and more accurate as the scale grows—is not new to mathematics. Systems in probability, such as coin flipping, behave in this way. It is impossible to predict the result of a single coin flipping, but over time, if the coin is unbiased, it will come up heads half the time. What is surprising is that the prime number system is not probabilistic, but it still behaves in many ways as if it were randomly selected.
Summary: Who Wants to be a Millionaire?
Number theory, which includes the study of prime numbers, is rich with unsolved problems, unsuccessfully tackled by the greatest minds for hundreds of years. A few of those open problems are mathematical statements that have not been proven yet, but in whose correctness, we strongly believe. Such unproven theorems are called “conjectures” or “hypotheses.” We already mentioned the conjecture regarding the existence of infinitely many twin primes—pairs of prime numbers a distance of two apart. Another well-known conjecture, called Goldbach’s conjecture, states that every even number can be written as a sum of two prime numbers. For example: 16 = 13 + 3, 54 = 47 + 7. If you manage to prove any of them, you will win eternal fame.3
Arguably the most famous unsolved problem in mathematics, Riemann’s hypothesis, was proposed by the same Bernhard Riemann who was mentioned earlier. In Riemann’s only research paper on prime numbers, published in 1859, Riemann stated a hypothesis that predicted how far from the true value of π(x), the number of primes up to x, was the approximation given by the prime number theorem. In other words, what can be said about the “error term” in the prime number theorem—the difference between the real quantity and the suggested formula? The Clay Foundation has named this problem as one of the seven problems for which it will pay a $1,000,000 prize for the solution! If you were not intrigued so far, maybe this prize will motivate you…
Why is this important? Who does it interest? Mathematicians judge their problems first and foremost by their difficulty and intrinsic beauty. Prime numbers score high in both of these criteria. However, prime numbers are also useful in a practical way. Research on prime numbers has found an important use in encryption (the science of encoding secret messages) in the past few decades. We mentioned earlier the fictional book by Carl Sagan, on an extraterrestrial culture communicating with mankind using prime numbers. But there is a much “hotter” area, not fictional whatsoever, that uses prime numbers for either civilian or military purposes; that is, encrypted transmissions. When we withdraw money from an ATM, we use a debit card, and the communication between us and the ATM is encrypted. Like many other codes for encryption, the one found on almost every debit card, called RSA (named after its inventors—Rivest, Shamir, and Adleman), is based on the properties of prime numbers.
The story of prime numbers is still surrounded with mystery. So, their story is not yet over and done with…
Glossary
Composite Number: ↑ a whole number that can be written as a product of two smaller numbers, for example, 24 = 3 × 8.
Prime Number (Non-Composite): ↑ a whole number that cannot be written as the product of two smaller numbers, such as 7 or 23.
Mathematical Proof: ↑ a series of logical arguments meant to prove the truth of a mathematical theorem. The proof is based on basic assumptions that were tested, or on other theorems that were previously proven.
Mathematical Theorem: ↑ a claim expressed in the language of mathematics that can definitely be said to be valid or invalid in a certain system.
Mathematical Conjecture: ↑ (also called a hypothesis)—a mathematical statement that is believed to be true but has not yet been proven. The “belief in validity” can result from checking special cases, computational evidence, or mathematical intuition. There are mathematical conjectures over which people still disagree.
Twin Primes: ↑ a pair of prime numbers with a difference of two, such as 5, 7 or 41, 43.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Further Readings
[1] ↑ Du Sautoy, M. 2003. The Music of the Primes. HarperCollins.
[2] ↑ Doxiadis, A. 1992. Uncle Petros and Goldbach’s Conjecture. Bloomsbury.
[3] ↑ Pomerance, C. 2004. “Prime numbers and the search for extraterrestrial intelligence,” in Mathematical Adventures for Students and Amateurs, eds D. Hayes and T. Shubin (M.A.A), 1–4.
[4] ↑ Singh, S. 1999. The Code Book. London, Fourth Estate.
Footnotes
[1] ↑ The division of the circle into 360 appears for the first time in the writings of Greek and Egyptian astronomers, but is based on an earlier division of the hour to 60 min by the Babylonians. Undoubtedly, it is also related to the fact that the solar years last 365 days (on average), but note that 365 = 5 x 73 and since both 5 and 73 are prime, 365 admits much fewer factorizations than 360.
[2] ↑ A correct reading of a mathematical text is an “active reading,” where the reader checks what is being said, computes examples, etc. But, if you would like to skip the proposed task, you can do so, and we will return to it and discuss it later on.
[3] ↑ The twin prime conjecture witnessed in recent years amazing breakthroughs by Zhang and Maynard but is nevertheless still open. Concerning the Goldbach conjecture, Helfgott proved in 2014 that every odd number larger than 5 is the sum of three primes.