摘要
质数在人类文明早期就引起了人们的注意。我们将解释质数是什么, 为什么对质数的研究让数学家和业余数学爱好者如此着迷;我们也将为你打开通往数学家世界的那扇窗。在人类文明史的开端, 质数就激起了人们的好奇心。质数是什么?为什么与之相关的问题如此难解?关于质数最有趣的问题之一就是它们在自然数之中的分布。在小的尺度上, 质数的出现似乎是随机的, 但在大的尺度上, 它们好像又遵循着某种模式, 我们至今仍未完全理解它。在这篇短文中, 我们会追溯自古代起的质数研究史, 并借机深入数学家的世界。
合数和质数
你是否考虑过: 为什么要将一天恰好分为 24 小时, 将圆周分为 360 度?其实 24 这个数字有个很有趣的性质: 它可以以较多的方式被分为若干完全相等的部分。例如, 24 ÷ 2 = 12, 24 ÷ 3 = 8, 24 ÷ 4 = 6 等等(你可以自己把剩下的分法都写出来!)这意味着一天可以分成两个相等的部分, 每个部分 12 小时, 对应白天和夜晚。对于一个 8 小时轮班不间断工作的工厂, 每一天也可以被恰好分为 3 个班次。
这也是将圆周分为 360 度的原因。如果把圆周分为两个, 三个, 四个, 十个, 十二个, 或者三十个相等的部分, 每部分的度数就都为整数;当然还有其它我们没提到的分割圆周的方法。在古代, 为了艺术、天文和工程等领域的需要, 将圆周高精度地分为若干相等大小的扇形是非常必要的。这项工作具有很大的实用意义, 而过程中除了圆规和量角器外就没有别的可用的工具了1。
可以写成两个较小的、不等于 1 的正整数的乘积的正整数, 就叫做合数。例如, 等式 24 = 4 × 6 和 33 = 3 × 11 就表明 24 和 33 是合数。无法以这种方式分解的非 1 正整数就称作质数。
2, 3, 5, 7, 11, 13, 17, 19, 23 和 29
都是质数。事实上, 它们就是前 10 个质数(如果愿意的话可以自己检查一下!)。
观察这一小列质数就足以有些有趣的发现。首先, 除了 2 之外, 所有的质数都是奇数, 这是因为偶数能被 2 整除, 这使得除了 2 之外的偶数都是合数。因此, 任何两个连续的比 2 大的质数之间的距离至少是 2。在这一小列质数中, 我们可以找到连续的两个质数, 其差恰好为 2(例如 3 和 5, 17 和 19)。连续的两个质数的差也可以比较大, 比如 23 和 29 之间就相差 6, 而之间的 24, 25, 26, 27, 28 都是合数。另一个有趣的发现是, 在第一个和第二个由连续 10 个正整数构成的组中(也就是说 1-10 和 11-20)都有 4 个质数, 但是在第三个组中(也就是说 21-30)只有两个质数。这意味着什么呢?随着数的增大, 质数会变得更稀少吗?有人能断言我们能不停地找下去, 找到无穷多个质数吗?
如果在这时, 有什么发现让你感到兴奋, 而且想继续研究质数序列和我们刚提出的问题, 这就意味着你的思维已经像个数学家了。停!先别急着往下看2!拿支笔, 拿张纸, 把 1 到 100 的数都写下来, 再把质数标出来。看看有多少组相差为 2 的质数, 看看每连续 10 个数中有多少质数。你能发现什么规律吗?或者说不超过 100 的这些质数显得杂乱无章呢?
一些史话和一个定理
质数自古时起就吸引了人们的注意, 甚至被人们和超自然现象联系在一起。即使在今天, 在现代, 也有很多人赋予质数以神秘的属性。著名的天文学家、作家卡尔 ⋅ 萨根于 1985 年写了一本名为《超时空接触》的书, 讲述了外星文明试图用质数作为信号和人类交流。这种用基于质数的信号作为与外星文明沟通方式的想法, 至今仍不停激起人们的想象力。
人们普遍认为, 在毕达哥拉斯时代, 人们就已产生对质数的浓厚兴趣。毕达哥拉斯是古希腊的数学家。他的学生组成的毕达哥拉斯学派生活在公元前六世纪, 其中一部分是科学家, 另一部分是神秘主义者。他们并没留下文字记载;我们对他们的了解都来自口耳相传。三百年后的公元前三世纪, 亚历山大(现在位于埃及)是希腊世界的文化中心。你也许听说过拖勒密一世时期住在亚历山大的欧几里得(图 1), 因为欧几里得几何就得名于他。欧几里得几何学已在学校中教授了 2000 多年。但欧几里得也对数论很感兴趣;他在著作《元素》的第九册命题 20 中, 给出了 ''质数有无穷多个'' 这个定理的第一个数学证明。

- 图 1 - 和质数有关的人物。
这时谈一谈定理和数学证明这些概念正合适。定理是指用数学语言所作的陈述, 具有要么成立要么不成立的确定性。比方说, ''质数有无穷多个'' 这个定理断言在自然数序列(1, 2, 3, ……)中质数序列是无限长的。更确切地说, 这个定理是说如果我们写出一个有限的质数序列, 我们总能找到另一个质数不在原有的序列中。要证明这个定理, 仅仅对特定给定的有限质数序列, 指出有另一个不同的质数, 是不够的。例如, 如果我们对于前 10 个质数构成的序列, 指出 31 是质数但不在这个序列之中, 我们的确说明了这个序列不包含所有的质数。但也许把 31 加进来后我们就找到了所有的质数, 而没有别的了。我们需要做的, 也恰恰是欧几里得 2300 年前做的, 是给出一个令人信服的论证——为什么对于任何有限的质数序列, 不论它有多长, 都能找到不在其中的质数。在下一部分中我们会介绍欧几里得的证明, 而且不涉及太多细节, 免得读起来无聊。
欧几里得 ''质数有无穷多个'' 的证明
为了证明存在无穷多个质数, 欧几里得使用了他已知的另一个基本定理, 即 ''任何一个自然数都可以写成质数的乘积'' , 而这个论断很容易证明是对的。如果你选出一个大于 1 的正整数, 它不是合数的话, 那它本身就是质数了。否则, 它就可以写成两个较小正整数的乘积。如果两个较小数都是质数, 那原数就已经分成两个质数的乘积了;如果不是的话, 就把较小数分成比它更小的数的乘积, 如此下去。在此过程中, 乘积中的合数持续被更小的数替换掉。因为不可能永远分下去, 所以这个过程必须在某一步停下来, 此时所有得到的较小数都不能再分了, 这意味着它们都是质数。举个例子, 我们把 72 分成素因数的乘积:
72 = 12 × 6 = 3 × 4 × 6 = 3 × 2 × 2 × 6 = 3 × 2 × 2 × 2 × 3
基于这个基本事实, 我们就能解释欧几里得对于质数集无限的优美证明了。我们将用前十个质数构成的序列来演示这个想法, 但请注意, 同样的想法也适用于任何有限的质数序列。我们把序列中所有的数乘起来, 并把结果加上 1。把得到的数称作 N。(事实上 N 是多少并不重要, 因为这个论证对任何质数序列都适用)。
N = (2 × 3 × 5 × 7 × 11 × 13 × 17 × 19 × 23 × 29)+1
N 和其它大于 1 的自然数一样, 可以写成质数的乘积。它们是哪些数呢?或者说 N 的质因数是哪些呢?我们不知道, 因为我们还没做计算, 但有一件事我们能确定: 它们都能整除 N。然而, 用我们的序列 2, 3, 5, 7, ……, 23, 29 中的任何一个质数除 N 的时候, 都会余 1。我们假定这是所有质数构成的序列, 却发现它们都不整除 N。所以 N 的质因数并不在序列当中, 确切地说, 一定存在超过 29 的新质数。
埃拉托斯特尼筛法
小于 100 的质数你都找全了吗?用的是哪种方法呢?你是不是逐个去考察每个数, 看它是否能被较小的数整除?用这种方法的话, 肯定非常耗时。埃拉托斯特尼(图 1)是希腊化时代最伟大的学者之一, 生活于欧几里得之后的几十年。他曾担任亚历山大图书馆首席图书管理员。这是史上第一个图书馆, 也是古代世界最大的图书馆。除数学外, 他对天文, 音乐和地理都兴趣浓厚, 他是彼时第一个以令人难以置信的准确度计算地球周长的人。除此之外, 他提出了一种聪明的方法来找出给定范围内所有质数。由于这种方法的思想是筛去所有的合数, 我们称其为埃拉托斯特尼筛法。
我们以小于 100 的质数序列(但愿它们还在你眼前)为例演示埃拉托斯特尼筛法(图 2)。把 2 圈起来, 因为它是第一个质数, 然后把所有比 2 大的 2 的倍数擦掉, 也就是所有的偶合数。继续看下一个没擦掉的数——3, 它还留着, 不能写成较小数的乘积, 可以把它圈起来, 因为它是质数。同样地, 把比 3 大的 3 的倍数都擦掉。请注意, 其中有些数(比如 6)已经被擦掉了, 而另一些(比如 9)现在正要擦掉。圈出下一个没擦的数——5, 和前面一样, 擦去所有比 5 大的 5 的倍数, 其中 10, 15 和 20 已被擦了, 但 25 和 35 现在才要擦。用同样的方式继续下去——到什么时候呢?其实, 从 10 附近的数(也就是 7)开始进行一轮后就不需要继续下去了。试着想想为什么。这时, 所有没擦掉的小于 100 的数都是质数, 可以都放心地圈出来了!
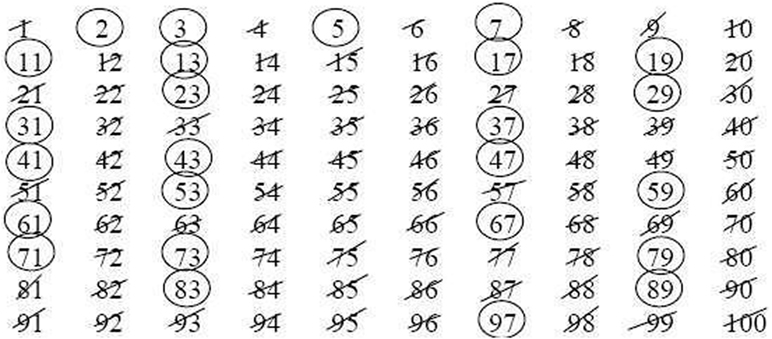
- 图 2 - 埃拉托斯特尼筛法。
- 合数均被划去而质数均被圈出。
质数的频率
质数出现的频率有多大呢? 1, 000, 000 到 1, 001, 000(一百万到一百万零一千)之间大约有多少质数呢? 1, 000, 000, 000 到 1, 000, 001, 000(十亿到十亿零一千)之间又大概有多少呢?我们能否估计一万亿(1, 000, 000, 000, 000)到一万亿零一千质数的数量呢?
计算表明随着数的增大, 质数变得越来越稀少。但是, 我们是否有可能找到一个准确的定理来精确刻画它们的稀有程度?最初是伟大的数学家卡尔 ⋅ 弗里德里希 ⋅ 高斯于 1793 年, 也就是他 16 岁的时候, 以猜想的形式提出了这个定理。十九世纪数学家伯恩哈德 ⋅ 黎曼(图 1)发明了研究质数的诸多工具, 对质数的现代研究工作产生了极大的影响。但是, 这个定理的正式证明在 1896 年才给出, 而这距离它被提出已有一个世纪了。同一年, 法国的 Jacques Hadamard 和比利时的 delaVallée-Poussin(图 1)这两位数学家提供了两个互不相关的证明, 这着实令人惊讶。更有趣的是, 两人都是大约在黎曼去世时出生的。他们所证明的定理以其重要性而得名 ''质数定理''。
质数定理的确切表述和证明的详细过程需要用到高级的数学工具, 因此我们不在此展开讨论。但粗略地说, 质数定理表明 x 周围的质数出现的频率大约与 x 的位数成反比。在上面的例子中, 在一百万附近长度为 1000 的 ''窗口'' (我们是指一百万到一百万零一千之间的间隔)中的质数的数量, 会比十亿附近同样大的 ''窗口'' 中质数的数量多 50%,(这个比例为 9:6, 恰好就是十亿和一百万中 ''0'' 的个数之比), 也会比一万亿附近同样大的 ''窗口'' 中质数的数量多一倍(这里, 一万亿和一百万中 ''0'' 的个数比是 12:6)。实际上, 计算机的计算得出, 第一个窗口中有 75 个质数, 第二个窗口中有 49 个, 第三个窗口中, 也就是指介于一万亿和一万亿零一千之间, 只有 37 个。
这些信息也可以用图表来表示(图 3)。你可以看到在 x≤100 的范围内, 以及在 x≤1, 000 的范围内, 到 x 为止的质数的数量 π(x)如何变化。请注意, 我们沿 x 轴向右走, 每遇到一个新的质数, 曲线就会上升 1, 因此图像是阶梯状的(图 3A)。在小的尺度上看, 很难在图中发现规律——容易证明我们可以找到任意长的区间, 其中一个质数都没有, 这意味着这部分区间对应的图像曲线不会往上走。另一方面, 一个著名的猜想(见下文)断言: 存在无穷多对 ''孪生质数'' , 也就是差为 2 的质数对;这在图上即表现为宽度为 2 的阶梯。然而, 在大的尺度上看, 图像看起来很平滑(图 3B);这种大尺度上得到的平滑曲线就很好地展现了质数定理的内容。
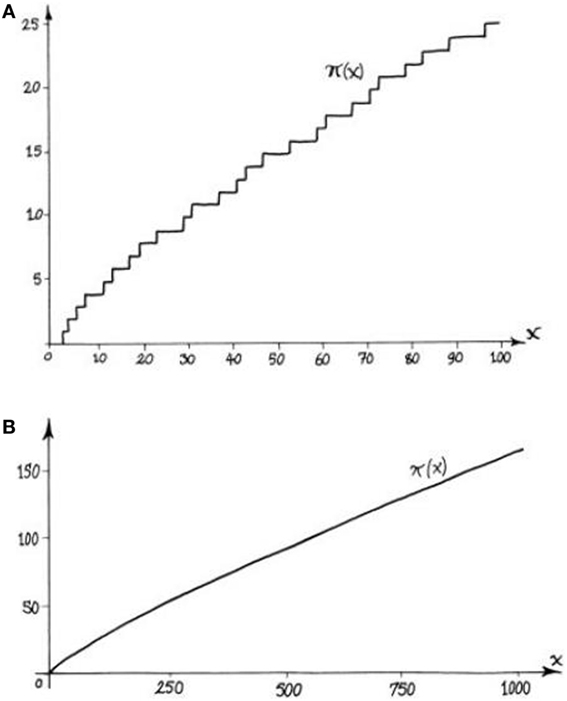
- 图 3 - 质数频率。
- 图像画出了 π(x), 也就是到 x 为止的质数个数。图像
(A) 中, x 从 0 取到 100, 图形呈现阶梯状。图像(B) 中, x 从 0 取到 1,000, 因此尺度更大, 曲线看起来就更平滑了。
事实上, 某些数学中的现象在一个尺度上看不出规律, 在另一个更大的尺度上却呈现出规律性(图像的平滑性), 也就是说随着规模增长, 规律越来越准确。这在数学中并不稀奇。而概率系统, 比如掷硬币的模型, 就表现成这样。不可能预测掷单个硬币是正是反, 但只要硬币是两面对称的, 随着时间增加, 就会有一半的时候正面向上。让人惊奇的是, 质数系统并不是随机性的, 但它在很多方面仍表现得似乎是随机选择的一样。
提要: 谁想成为百万富翁?
包括质数研究在内的数论领域处处是未解迷题;数百年来, 即使是最聪明的头脑屡屡挑战也未能破解。这些开放性的问题中有些数学命题尚未证明, 但我们却坚信它们是对的;我们把这些还没证明的定理称作 ''猜想'' 或 ''假设''。我们已经提到过 ''存在无限多对孪生质数——即差为 2 的质数对'' 的猜想。另一个有名的猜想也就是哥德巴赫猜想。它是说每个偶数(除了 2 以外)都可以写成两个质数的和。例如: 16 = 13 + 3, 54 = 47 + 7。如果你能证明这两个中的任何一个, 你定将名垂青史3。
''黎曼猜想'' 可以说是数学界最知名的未解谜题, 它的提出者伯恩哈德 ⋅ 黎曼我们前面已经提到过了。黎曼于 1859 年发表了他唯一的一篇研究质数的论文, 他在其中提出了一个猜想, 即估计了 π(x)(到 x 为止的质数个数)和质数定理给出的近似值之间差了多远。换句话说, 对质数定理中的 ''误差项'' , 也就是实际质数数量和近似公式之间的差, 我们能有些什么认识呢?克莱基金会把这个问题归为七大数学问题之一, 解决的人可以得到一百万美元的奖金!如果你到目前为止还不怎么感兴趣的话, 这个大奖也许能给你带来激励……
这个问题为什么重要呢?哪些人感兴趣呢?数学家评判一个数学问题的价值时, 主要基于问题的难度和问题本质中的美感。以这两条作标准, 质数的得分都很高。此外, 质数也有实用价值。过去几十年中的研究已经揭示出质数在加密(研究给机密信息编码的学科)中重要的作用。我们此前已提到卡尔 ⋅ 萨根的那部讲述外星文化用质数与人类进行联络的科幻著作, 但是, 在一个更热的领域——加密传输中, 质数被应用于民事及军事。这当然就不是科幻了。我们从 ATM 机取款用的是借记卡, 而我们和 ATM 机之间的信息传输都是加密的。和许多其它密码系统一样, 几乎所有借记卡用的都是 RSA(得名于发明者 Rivest, Shamir 和 Adleman)密码系统, 它基于的正是质数的性质。
质数的故事仍然充满着神秘色彩, 关于它们的故事还未完结……
词汇表
合数 (Composite Number): ↑ 可以写成两个较小正整数的乘积的正整数, 例如, 24 是合数, 因为 24 = 3×8。
质数 (Prime Number): ↑ 不能写成两个较小正整数乘积的正整数(1 除外), 例如 7 或 23。
数学定理 (Mathematical Theorem): ↑ 用数学语言所作的陈述, 在特定理论体系中具有要么正确要么不正确的确定性。
数学证明 (Mathematical Proof): ↑ 为证明数学定理的真实性的一系列逻辑论证过程。证明须基于已考察过的基本假设, 或者其它先前已经证明的定理。
数学猜想 (Mathematical Conjecture): ↑ (也称为假设)——数学中一种被认为可靠但尚未证明的陈述。产生 ''认为某猜想可靠'' 的感受, 往往是考察了特殊情况, 进行了计算或数学直觉带来的结果。也有一些数学猜想的正确性并不被人们认同。
孪生质数 (Twin Primes): ↑ 一对差为 2 的质数, 如 5, 7 或 41, 43。
利益冲突声明
作者声明, 该研究是在没有任何可能被解释为潜在利益冲突的商业或财务关系的情况下进行的。
脚注
1. ↑将圆划分为 360 度的做法首次出现在希腊和埃及天文学家的著作中, 但这是基于更早时巴比伦人将 1 小时划分为 60 分钟的做法。毫无疑问, 太阳年为 365 天(平均)这一事实也与之相关, 但请注意 365 = 5 × 73 并且由于 5 和 73 都是质数, 因此 365 比 360 的因式分解要少得多。
2. ↑正确阅读数学文本是一种 ''主动阅读'' , 读者会检查所说的内容、计算示例等。但是, 如果你想跳过这项任务, 可以这样做, 我们稍后会再讨论。
3. ↑孪生质数猜想近年来由于张和梅纳德的研究有了惊人的突破, 但仍然悬而未决。关于哥德巴赫猜想, 赫尔夫戈特在 2014 年证明了每个大于 5 的奇数都是三个质数之和。
参考文献
[1] Du Sautoy, M. 2003. The Music of the Primes. HarperCollins.
[2] Doxiadis, A. 1992. Uncle Petros and Goldbach’s Conjecture. Bloomsbury.
[3] Pomerance, C. 2004. ''Prime numbers and the search for extraterrestrial intelligence,'' in Mathematical Adventures for Students and Amateurs, eds D. Hayes and T. Shubin (M.A.A), 1–4.
[4] Singh, S. 1999. The Code Book. London, Fourth Estate.