תַקצִיר
פתרון מתמטיקה בסיסית נראה דבר די שכיח. 2+2 שווה 4, גם בצרפתית וגם בסינית. 8X7 שווה 56 גם בארצות הברית וגם בגרמניה. אף על פי שמרביתנו משתמשים באותם סמלים כדי לכתוב מספרים (... ,4 ,3 ,2 ,1), אנו משתמשים במילים שונות מאוד עבור המספרים האלה, פשוט מאחר שאנו מדברים בשפות שונות. במאמר הזה, ניתן דוגמאות לאיך נראות מילות מספרים בשפות שונות. גם נראה כיצד האופן שבו מילים רבּות-ספרות בנויות, יכול לגרום ללמידת מתמטיקה ולהתמודדות עם מספרים גדולים להיות קשות או קלות יותר.
מספרים ומתמטיקה הם די אוניברסליים
ביצוע מתמטיקה 1 בסיסית נראה דבר די שכיח – אתם עושים זאת, אנחנו עושים זאת, ואפילו ילדים קטנים עושים זאת לפני שהם הולכים לבית הספר, לדוגמה כשהם סופרים חלוקי נחל. זה גם נכון עבור חישובים: 2+2 שווה 4, גם בצרפתית וגם בסינית. 7 × 8 שווה ל-56, גם בארצות הברית וגם בגרמניה 2. מרבית המדינות משתמשות במה שנקרא מערכת מספרים הינדוּ-ערבית כדי לכתוב מספרים. מערכת המספרים ההינדו-ערבית משתמשת בעשרה סמלים בדיוק, שאתם ככל הנראה מכירים: 1, 2, 3, 4, 5, 6, 7, 8, 9, ו-0. אנו משתמשים בעשרת הסמלים האלה כדי לכתוב מספר חד-ספרתי, ואנחנו משלבים אותם כשאנו כותבים מספרים רב-ספרתיים.
מספרים רב-ספרתיים מקיימים את כלל ערך-מיקום, שמאפשר לנו לכתוב כמה מספרים שאנו רוצים עם עשרה סמלים בלבד שאנו כבר מכירים. כלל הערך-מיקום משמעותו שהערך של כל ספרה נעשה ברור כשאנו מסתכלים על המיקום של הספרה הזו בתוך מספר רב-ספרתי. לדוגמה, הערך של 9 במספר 92 הוא 90 (10 × 9) והערך של 2 במספר 92 הוא 2 (1 × 2). אולם ב-29 המצב הוא הפוך: הערך של 9 הוא פשוט 9 (1 × 9) והערך של 2 הוא 20 (1 × 2). זו הסיבה לכך ש-92 שונה מ-29, אף על פי ששניהם שילובים של אותן ספרות!
זה שיש את אותם חוקים ומספרים זה מצוין, מאחר שהדבר מקל על הדיבור על מספרים ועל חישובים. כמעט נראה כאילו שיש לנו שפה מתמטית עולמית אחת, ולמידת מתמטיקה בסיסית במדינה אחת היא מספיקה, ולא צריך ללמוד אותה שוב במדינה אחרת. 2 + 2 נשאר 4, לא משנה מהיכן אתם מגיעים.
שפות משׁיימות מספרים אחרת, וזה יכול להקל או להקשות על לימוד מתמטיקה
ישנה רק בעיה אחת קטנה. אף על פי שמרביתנו משתמשים באותם סמלים כדי לכתוב מספרים, אנו משתמשים במילים שונות מאוד עבור המספרים האלה. הסיבה לכך היא שאנו מדברים בשפות שונות. בטבלה 1, אתם יכולים למצוא דוגמאות של מילות מספרים עבור המספרים 10-1 בשפות שונות. אתם יכולים לראות, שמילות מספרים משתנות מאוד משפה לשפה – ממש כמו ששאר המילים משתנות בין שפות. היכרות עם השמות והמשמעויות של המספרים 10-1 בשפה שלכם היא אחד הצעדים הראשונים ביותר והחשובים ביותר בלמידת מתמטיקה. אולם למידת עשר מילות מספרים היא קשה עבור ילדים שמדברים שפות שונות. בסופו של דבר כולם צריכים ללמוד עשר מילים חדשות; אחת עשרה, אם אנו כוללים את 0 וגם את 10.
| Hindi | Basque | German | French | English | Mandarin | ||
| 0 | shuniye | zero, hutsa | null | zéro | zero | ling | 0 |
| 1 | ek | bat | eins | un | one | yi | 1 |
| 2 | do | bi | zwei | deux | two | èr | 2 |
| 3 | teen | hiru | drei | trois | three | sān | 3 |
| 4 | chat | lau | vier | quatre | four | sì | 4 |
| 5 | panch | bost | fünf | cinq | five | wǔ | 5 |
| 6 | cheh | sei | sechs | six | six | liù | 6 |
| 7 | saat | zazpi | sieben | sept | seven | qi | 7 |
| 8 | aath | zortzi | acht | huit | eight | bā | 8 |
| 9 | nao | bederatzi | neun | neuf | nine | jiǔ | 9 |
| 10 | das | hamar | zehn | dix | ten | shí | 10 |
| 11 | rah [oneteen] |
hamaika [ten one] |
[eleven] |
[oneteen] |
shí yi [ten one] |
11 | |
| 12 | rah [twoteen] |
hamabi [ten two] |
[twelve] |
[twoteen] |
shí èr [ten two] |
12 | |
| 13 | tehrah [thirteen] |
hamahiru [ten three] |
[three ten] |
[thirteen] |
shí sān [ten three] |
13 | |
| 16 | [sixteen] |
hamasei [ten six] |
[six ten] |
[sixteen] |
shí liù [ten six] |
16 | |
| 17 | satrah [seventeen] |
hamazazpi [ten seven] |
[seven ten] |
dix-sept [ten seven] |
shí qi [ten seven] |
17 | |
| 20 | bees [twenty] |
hogei [twenty] |
zwanzig [twenty] |
vingt [twenty] |
twenty | èr shí [two ten] |
20 |
| 21 | [one and twenty] |
hogeita bat [twenty and one] |
[one and twenty] |
vingt un [twenty and one] |
twenty-one | èr shí yi [two ten one] |
21 |
| 29 | [one before thirty] |
hogeita bederatzi [twenty and nine] |
[nine and twenty] |
vingt-neuf [twenty-nine] |
twenty-nine | èr shí jiǔ [two ten nine] |
29 |
| 48 | [eigth and forty] |
borrogeita zortzi [forty and eight] |
[eigth and forty] |
quarante-huit [forty-eight] |
forty-eight | sì shí bā [four ten eight] |
48 |
| 75 | [five and seventy] |
[sixty and ten five] |
[five and seventy] |
[sixty-fifteen] |
seventy-five | qi shí wǔ [seven ten five] |
75 |
| 97 | [seven and ninety] |
[eigthy and ten seven] |
[seven and ninety] |
quatre-vingt -dix-sept [four-twenty- ten-seven] |
ninety-seven | jiǔ shí qi [nine ten seven] |
97 |
| 100 | ek sau [one hundred] |
ehun [hundred] |
(ein)hundred [(one)hundred] |
cent [hundred] |
one hundred | yì bǎi [one hundred] |
100 |
- טבלה 1- מילות מספר בשפות שונות. אל תדאגו, אתם לא צריכים להסתכל על כל המילים בפירוט. אולי תתמקדו במילים הכחולות. לכל מילות המספר הכחולות יש משהו מיוחד בהשוואה למילות המספרים הרגילותבמנדרינית. מתחת לכל המילים של מספרים דו-ספרתיים, אתם יכולים לראות כיצד המספרים והמילים האלה ככל הנראה היו מתורגמים לאנגלית. האופן שבו חלק מהמילים האלה בנויות הוא די מורכב. אם אתם רוצים לדעת כיצד מילות המספרים האלה מבוטאות, אתם יכולים להקשיב להן באינטרנט. עבור מנדרינית, צרפתית, גרמנית והינדית בקרו ב: bing.com/translatorי והכניסו את מילת המספר. עבור באסקית, הסתכלו ביוטיוב: https://www.youtube.com/watch?v=6eb0J4Vg5ys&feature (מספרים 19-1) https://www.youtube.com/watch?v=wPbYCBzsw2A&feature (מספרים 39-20).
למידת מילות מספרים עבור מספרים גדולים מעשר משתנה מאוד בין שפות שונות (נסו לעשות את הבוחן שבאיור 1). בשפות מסוימות, האופן שבו אנשים משׁיימים מספרים רבי-ספרות הוא ברור מאוד ורגיל. מנדרינית (השפה המדוברת ביותר בסין) היא אחת השפות האלה. המילה המנדרינית למספר 29 משמעותה “שתיים-עשר-תשע”, והמילה למספר 97 משמעותה “תשע-עשר-שבע”. מדענים קוראים לשפות כאלה שקופות. משמעות הדבר היא שבמנדרינית מילות המספר מתאימות טוב לאופן שבו אנו כותבים את הספרות במספרים רב-ספרתיים, ומילות המספר מראות לנו בבהירות את כלל ערך המיקום: 97 = 9 × 10 + 7 = “-תשע- עשר-שבע”.
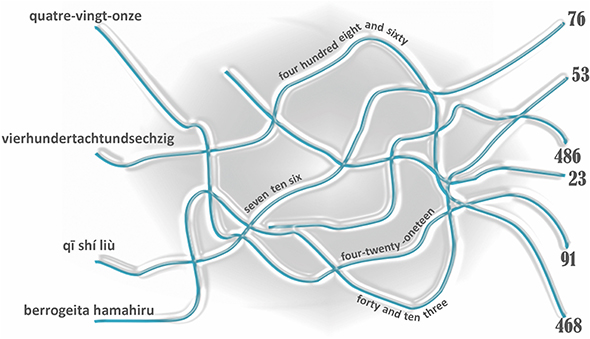
- איור 1 - אלה מילות מספר מצד שמאל שייכות לאיזה מספר הינדו-ערבי מימין? נסו להבין בעצמכם, ואז לעקוב אחרי הקו כדי לראות אם צדקתם.
- במאמר, ישנם כמה רמזים שיכולים לסייע לכם להבין את זה, וטבלה 1 עשויה גם לסייע לכם להבין את מילות המספר.
מדענים מצאו שלמידת מתמטיקה והתמודדות עם מספרים רב-ספרתייים קלה יותר לילדים שמדברים שפה עם מילות מספר ברורות. אולם הבעיה היא שלא לכל השפות יש מילות מספר ברורות. כיצד מילות מספר בלתי ברורות נראות? הסתכלו על חלק מהמילים עבור 97. בבאסקית (שפה שמדוברת בעיקר באזור של צפון ספרד), הם אומרים “laurogeita hamazazpi”, מה שאומר “שמונים-עשר-שבע” (80 + 17). בצרפתית, הם אומרים “quatre-vingt-dix-sept”, מה שאומר “ארבע-עשרים-עשר-שבע” (4 × 20 + 10 + 7). האופן שבו המספרים האלה נבנים הוא מורכב מאוד. בהינדית (אחת השפות הפופולריות ביותר בהודו), ישנם כמה מספרים שעבורם אנשים משתמשים בחיסור במקום בחיבור כדי לבנות מילת מספר. לדוגמה, עבור המספר 29 הם אומרים “unatis”, מה שאומר “אחת לפני שלושים” (30-1).
בטבלה 1, אתם יכולים לראות את המילים עבור חלק מהמספרים הרב-ספרתיים בשפות שונות. כל מילות המספרים הכחולים הן ייחודיות בצורה כלשהי. מספרי העשׂרה קשים במיוחד ללמידה בשפות שונות. האם לא היה ברור יותר לומר “אחת-עשר-שתיים” מאשר “שתיים עשרה” עבור 12? שתיים עשרה היא מילה חדשה שאנו צריכים ללמוד, בעוד שעבור “אחת-עשר-שתיים” אנו פשוט יכולים להשתמש בכלל. אמירת “ארבע עשרה” במקום “עשר ארבע” (או אפילו “אחת-עשר-ארבע” כמו במנדרינית) זה גם לא כל כך מסייע. מדוע אנו לפעמים מחליפים את סדר המספרים ואומרים קודם כל את היחידות? החלפה כזו נקראת חילוף מילת מספר. באנגלית, רק כמה מספרי עשרה (שלוש עשרה ותשע עשרה) מוחלפים. בשפות אחרות כמו גרמנית, הולנדית, ערבית, או מלטזית, כל המספרים הדו-ספרתיים מוחלפים (97 זה “siebenundneunzig” בגרמנית, מה שאומר “שבע ותשעים”). עבור מספרים גדולים יותר, זה נעשה אפילו מבלבל יותר! המילה הגרמנית ל-234 משמעותה “שתיים-מאה-ארבע-ושלושים”. כאן, הספרה מצד שמאל במספר נאמרת קודם, אז הספרה מימין, ולבסוף הספרה שבאמצע. מורכב, לא?
לא מפתיע שילדים שמדברים שפות עם מילות מספר מוחלפות מתקשים להתמודד עם מספרים רב-ספרתיים. ילדים גרמניים (נדרשת החלפה) טועים יותר מפי 5 כשהם כותבים מספרים מאשר ילדים יפנים (לא נדרשת החלפה) [1]. כמחצית מהטעויות אצל ילדים גרמנים מערבות בלבול של הסדר [2]. לדוגמה, כאשר הם שומעים “חמש וארבעים” הם לעיתים קרובות כותבים 54 ולא את המספר הנכון, 45. אם כן, כל הילדים שגדלים עם מערכת מילות מספר שקופה יכולים להיות שמחים שקל להם יותר ללמוד את המספרים.
אולם אחרי אימון, אנשים פשוט לומדים איך לעשות את זה
אנו כבר יודעים שלילדים שמדברים שפה עם מילות מספר לא שקופות קשה יותר ללמוד מתמטיקה ביחס לילדים שמדברים בשפות עם מילות מספר שקופות. אולם למרבית הילדים הגדולים יותר והמבוגרים כבר אין בעיות כאלה. אם למידת מילות מספר לא שקופות היא רק עניין של זמן או של תרגול נוסף, האם זו באמת בעיה? אף על פי שמרבית הילדים לומדים להתמודד עם זה מהר, אחרים ממשיכים להתקשות. לדוגמה מחקר אחד הראה שילדים שמתקשים עם מילות מספר בערך בגיל שבע צפויים לחוות בעיות עם מתמטיקה שלוש שנים מאוחר יותר [3]. אם כן, התקשות עם מילות מספר יכולה להראות לנו אלה ילדים עשויים להצטרך סיוע נוסף עם מתמטיקה, כך שהם לא ישארו מאחור. ככל שאנו מסייעים מוקדם יותר, כך טוב יותר!
... אולם בעיות מתחילות מחדש כשאנשים מנסים לעשות מתמטיקה בשפה אחרת!
יותר ויותר אנשים מטיילים כעת או אפילו חיים במדינות אחרות שבהן הם צריכים לדבּר בשפות אחרות. לעיתים, לשפה החדשה יש צורה אחרת להגיד מילים של מספרים דו-ספרתיים, ועלינו ללמוד את מילות המספר החדשות האלה בעל פה. זה יכול להיות בעיה גדולה, לדוגמה אם אתם מגיעים מפולין (לא נדרשת החלפה), ואתם רוצים לגור בגרמניה (נדרשת החלפה). Krzysztof, אחד המחברים של המאמר הזה, הוא אחד האנשים האלה. בכל פעם שהוא קונה את המצרכים שלו ומנסה לשלם עבורם, הוא מתבלבל. כשהאישה בדלפק אומר “Neunundzwanzig euro, bitte” [תשע ועשרים יורו, בבקשה!], המחשבה הראשונה של Krzysztof היא “כיצד לעזאזל הצלחתי לבזבז כמעט מאה יורו על מזון שאני מתכנן לאכול בשלושת הימים הבאים?”. אף על פי שהוא יודע שעליו לעשות את ההחלפה, ואף על פי שהוא עורך את המחקר על הנושא הזה עצמו, בדרך כלל לוקח לו זמן מה להירגע ולשלם את כמות הכסף המתאימה.
למידת מילות מספר בשפה חדשה היא התחלה טובה, אף על פי שזה כבר עשוי להיות מתעתע. אולם אפילו אם אתם יודעים את כל מספרי המילים בשפה חדשה, זה לא אומר שאתם תרצו לעשות מתמטיקה בשפה החדשה הזו. בדרך כלל, אנשים מעדיפים לפתור מתמטיקה בשפה אחת, ובמרבית המקרים הם לא רוצים לפתור מתמטיקה בשפה שהם רק למדו לדבר בה. יותר סביר שאנשים יבצעו מתמטיקה בשפה הראשית שלהם, או בשפה שבהם הם למדו לעשות מתמטיקה בבית הספר.
מסקנות
אנו משתמשים במספרים ובמילות מספר בכל יום, ועבור מרביתנו הן לא ממש מיוחדות – לפחות לא אחרי זמן מה של תרגול. אולם כשאנו מסתכלים על מילות מספר מקרוב יותר, מרתק לראות כיצד שפות שונות בשׁיוּם של מספרים רב-ספרתיים. אף על פי שמילות מספר שונות מאוד, במרבית המקרים האופן שבו מילות מספר בנויות אינו מקרי אלא עוקב אחרי כללים מסוימים. התבוננו שוב בבוחן שבאיור 1. כעת משלמדתם כמה מהחוקים האלה, תראו אם אתם יכולים לפענח חלק מהמספרים בקלות יותר. חקירת הפרטים של מילות מספר יכולה לסייע לנו להבין מדוע ילדים שמדברים שפה אחת עשויים להתקשות עם מתמטיקה יותר מילדים שמדברים בשפה אחרת. אנו עשויים גם להיות מסוגלים לזהוֹת ילדים שיש להם בעיות במתמטיקה בשלב מוקדם ולהבין כיצד לתמוך בהם. כמובן, החוקים של בניית מילות מספר אינם הדבר היחיד שחשוב כשלומדים מתמטיקה, אולם זו בהחלט פיסה מעניינת של הפאזל.
מילון מונחים
מערכת מספרים הינדו-ערבית (Hindu-Arabic Numeral System): ↑ סֶט של סמלים שמשמש לכתוב מספרים במרבית המדינות. מערכת המספרים ההינדו-ערבית משתמשת ב-10 סמלים בדיוק: 1, 2, 3, 4, 5, 6, 7, 8, 9, ו-0. אנו משתמשים בעשרת הסמלים האלה כדי לכתוב מספרים חד-ספרתיים, ואנו משלבים אותם כשאנו כותבים מספרים רב-ספרתיים.
כלל ערך-מיקום (Place-value Rule): ↑ כלל שמאפשר לנו לכתוב כמה מספרים שאנו רוצים באמצעות 10 סימנים שאנו כבר מכירים 1, 2, 3, 4, 5, 6, 7, ,8, 9, ו-0). כלל הערך-מיקום משמעותו שהערך של כל ספרה נעשה ברור כשאנו מסתכלים על המיקום של הספרה בתוך מספר רב-ספרתי. לדוגמה, הערך של 9 במספר 92 הוא 90 (9 × 10) והערך של 2 במספר 92 הוא 2 (2 × 1). אולם, ב-29 המצב הוא הפוך: הערך של 9 הוא פשוט 9 (9 × 1) והערך של 2 הוא 20 (2 × 1). זו הסיבה לכך ש-92 שונה מ-29, אף על פי ששניהם שילובים של אותן ספרות!
שקוף (Transparent): ↑ שקוף היא מילה אחרת לבהיר או בנוי טוב. בהקשר למילות מספר, המילה שקוף משמשת כדי לתאר שפות שבהן מילות המספר מתאימות בצורה טובה לאופן שבו אנו כותבים ספרות של מספרים רב-ספרתיים. בשפות שקופות מילות המספרים מראות בצורה ברורה את כלל הערך-מיקום (למשל, 97 = 9 × 10 + 7 = “תשעים ושבע”).
חילוף מילת מספר (Number Word Inversion): ↑ בחלק מהשפות, הסדר של מספרים דו-ספרתיים מוחלף. לדוגמה, במקום להגיד ארבעים ושתיים עבור המספר 42, בחלק מהשפות אומרים שתיים וארבעים. ההחלפה הזו נקראת היפוך מילת מספר.
הצהרת ניגוד אינטרסים
המחברים מצהירים כי המחקר נערך בהעדר כל קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.
תודות
אנו מודים ל-Ani, בת 11, עבור הערותיה על גרסאות קודמות של כתב היד. אנו רוצים להודות לאלה שסייעו בתרגום המאמרים באוסף הזה כדי לעשותם נגישׁים יותר עבור ילדים מחוץ למדינות דוברות אנגלית, ולקרן ג’ייקובס על סיפוק הכספים הנדרשים לתרגום המאמרים. בגין המאמר הזה, אנו רוצים להודות במיוחד לניינקה ון אטאסאלדט ולסבינה פיטרס על התרגום להולנדית.
הערת שוליים
1 ↑ Maths הוא קיצור של המילה mathematics שמשתמשים בו בבריטניה. בארצות הברית, הקיצור הוא math.
2 ↑ ה- “x” ב-7×8 הוא סמל לכפל. אולם, אנשים גם משתמשים ב“⋅” (7 ⋅ 8) או ב-“*” (7 * 8) במקום.
מקורות
[1] ↑ Moeller, K., Zuber, J., Olsen, N., Nuerk, H.-C., and Willmes, K. 2015. Intransparent German number words complicate transcoding–a translingual comparison with Japanese. Front. Psychol. 6:740. doi: 10.3389/fpsyg.2015.00740
[2] ↑ Zuber, J., Pixner, S., Moeller, K., and Nuerk, H.-C. 2009. On the language-specificity of basic number processing: transcoding in a language with inversion and its relation to working memory capacity. J. Exp. Child Psychol. 102:60–77. doi: 10.1016/j.jecp.2008.04.003
[3] ↑ Moeller, K., Pixner, S., Zuber, J., Kaufmann, L., and Nuerk, H.-C. 2011. Early place-value understanding as a precursor for later arithmetic performance–a longitudinal study on numerical development. Res. Dev. Disabil. 32:1837–51. doi: 10.1016/j.ridd.2011.03.012
