תַקצִיר
מתמטיקה היא נושא חשוב בבית הספר ובחיי היומיום (אתם יודעים זאת מתוך העיסוק בדמי הכיס שלכם וחישוב מספר הימים שנותרו בבית הספר עד לחופשות). עבור חלק מהילדים מתמטיקה מובנת בקלות – הם פשוט קולטים אותה ונהנים ממנה. אולם עבור ילדים אחרים למידת מתמטיקה היא קשה מאוד, ואפילו אם ניתנת להם עזרה נוספת עדיין קשה להם “לקלוט את זה” . לדוגמה, בעיה חשבונית כמו 2+2 יכולה להיפתר בקלות על-ידי שליפת התשובה מהזיכרון; אולם עבור חלק מהילדים הבעיה הזו דורשת הרבה עבודה קשה. באותה העת, הילדים האלה עשויים להיות טובים מאוד במקצועות אחרים שאינם דורשים שימוש במתמטיקה.
לילדים בעלי קשיים גדולים בלמידה של חשבון פשוט עשויה להיות בעיית למידה שאיננה מֻכֶּרֶת לרבים ששמה דיסקלקוליה התפתחותית (developmental dyscalculia). ילדים עם דיסקלקוליה הם בעלי יכולות מתמטיות נמוכות בהרבה מאשר חבריהם בני אותו הגיל. נוסף על כך הקשיים שלהם הם ארוכי טווח ואי אפשר להסביר אותם על-ידי הוראה לא טובה או על-ידי לקויות מוחיות אחרות. אף על פי שעשויים להיות לכם קשיים בלמידת מתמטיקה בזמנים שונים במהלך השיעור, ילדים עם דיסקלקוליה חוֹוים קשיים רבּים כל הזמן: פשוט קשה להם ללמוד מתמטיקה בכל הנסיבות. חשוב לדעת את זה מאחר שחלק מהילדים מתקשים בהבנה של מתמטיקה בחלק מהזמן, אבל בשלב כלשהו הם מבינים אותה. לילדים אלה אין דיסקלקוליה [1]. מדובר רק בילדים שממשיכים באופן קבוע לחוות בעיות, להם יש קושי אמיתי שנקרא, כאמור, דיסקלקוליה התפתחותית.
בקֶרֶב ילדים קטנים עם דיסקלקוליה שכיח מאוד השימוש בשיטות חלופיות לפתרון של בעיות מתמטיות (כמו למשל ספירה בעזרת האצבעות), שהן איטיות מאוד, בעוד שחבריהם לכיתה שאין להם דיסקלקוליה זוכרים את התשובות בלי להידרש לחשב אותן מחדש בכל פעם. עבור אותם החברים, התשובה פשוט “קופצת בראשם” – יש להם זיכרון טוב למִסְפרים ולעובדות.
מדוע ילדים מפתחים דיסקלקוליה התפתחותית?
עד כה מחקרים מעטים מאוד התייחסו לשאלה זו. זו שאלה שקשה מאוד לענות עליה מאחר שמדובר בלקוּת הטרוגנית, כלומר ישנם גורמים רבים שמשפיעים עליה, והיא מופיעה בצורה שונה אצל ילדים שונים. כיום יש לחוקרים ראיות שתומכות ברעיונות שונים ביחס לסיבות שבגינן חלק מהילדים מתקשים כל כך במתמטיקה. חלק מהאנשים מאמינים כי הגורם העיקרי אשר עומד בבסיס הדיסקלקוליה הוא זיכרון גרוע; זו, לטענתם, הסיבה לכך שכאשר אותם הילדים לומדים לראשונה לבצע חישובים חשבוניים פשוטים כמו 2+2, הם משתמשים באסטרטגיות ספירה כל פעם, ואינם מצליחים לשלוף את התשובה באופן מיידי בלי לחשוב או להשתמש באצבעותיהם [1]. כתוצאה מכך, הם אינם מסוגלים לאחסן בזיכרון את העובדה החשבונית הרלוונטית (למשל ש 4=2+2), ואינם מסוגלים לשלוף אותה בפעם אחרת. לחוקרים אחרים יש רעיונות שונים לגבי הגורמים לדיסקלקוליה. הם מסתכלים על גורמים אשר קשורים ביכולת הבסיסית שלנו להבין מהם מִסְפרים ומה משמעותם. בפרט, הם חושבים שהמערכת במוח אשר מסייעת לילדים להבין את המשמעות של מספרים (הבנה שהמספר “3” מתייחס לשלושה דברים; ראו איור 1A) אינה מתפתחת כראוי אצל ילדים עם דיסקלקוליה [2]. אם כן, חוקרים אלה חושבים שמקור הבעיה הוא בהבנה של המספרים ולא בזיכרון של הילדים, והיא זו שגורמת לקשיים בשימוש במספרים בפתרון של בעיות מתמטיות. חשבו על זה כמו על פאזל: אם לא יודעים לחבֵּר יחד את החתיכות, לא מצליחים להרכיב את הפאזל. בדומה לכך, אם לא יודעים מה המשמעות של מספרים, אי אפשר לבצע איתם חישובים. בעקבות כך חוקרים מנסים להבין מדוע חלק מהילדים מתקשים כל כך בחישוב של 2+2, זאת באמצעות התבוננות על האופן שבו הם מבינים את המשמעות של מספרים.
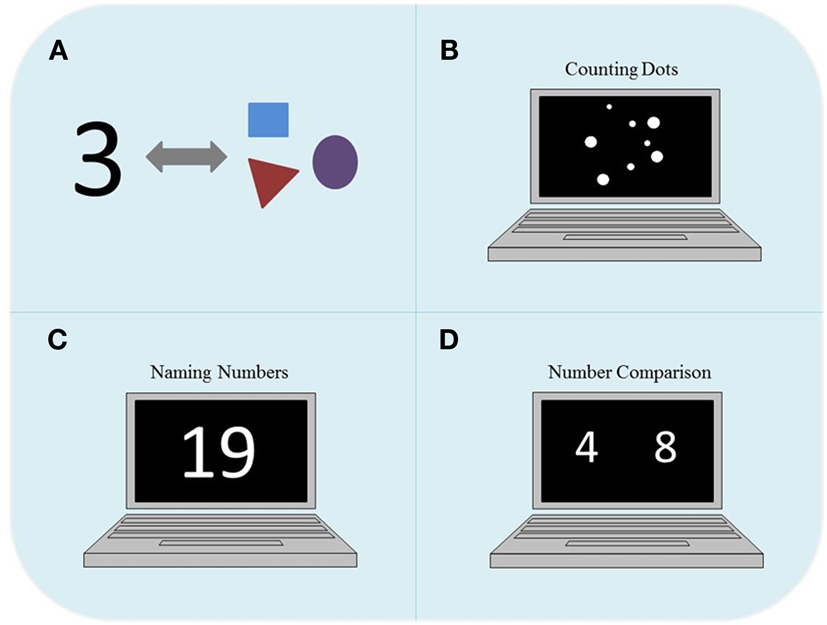
- איור 1 - A. מה המשמעות של מספרים?
- בתמונה A המספר 3 מצביע על כך שישנם שלושה פריטים, כמו למשל שלוש צורות שונות. אפשר להשתמש בפעילויות שונות שקשורות במספרים, למשל כמו אלה שבתמונות D-B, כדי למדוד עד כמה ילדים מבינים את המשמעות של מספרים. B. במהלך משימות של ספירת נקודות, מוצגת על מסך מחשב קבוצה של נקודות והילדים מתבקשים לספור הכי מהר שהם יכולים את כמות הנקודות הכוללת. C. במשימות של שִיוּם מספרים, מוצג מספר על המסך והילדים מתבקשים לכנות את המספר בשמו, במהירות המרבית האפשרית. D. משימות השוואת המספרים מנוהלות על מסך מחשב כפי שמוצג לעיל, ובהן ילדים ממקמים את אצבעותיהם על שני כפתורים: הם לוחצים על הכפתור השמאלי אם המספר הגדול יותר מופיע בצד שמאל ועל הכפתור הימני אם המספר הגדול יותר נמצא בצד ימין של המסך.
האם למספרים יש משמעות עבור ילדים עם דיסקלקוליה?
ישנוֹ מחקר אשר מראה כי הבנה של מספרים (לדוגמה, ידיעה שהמספר 2 מייצג שני דברים בעולם) היא בעייתית עבור ילדים עם דיסקלקוליה, וכתוצאה מכך הם אינם מסוגלים לפתור בקלות בעיות חיבור פשוטות כמו 2+2. חוקרים השתמשו במגוון פעילויות כדי להסתכל על מידת ההצלחה של ילדים בהבנה של מספרים. חלק מהדוגמאות כולל את הפעילויות האלה: ספירת נקודות, כאשר הילדים סופרים את כמות הנקודות שמוצגות על מסך מחשב (ראו איור 1B); שִׁיּוּם מספרים, כאשר הילדים מכנים את המספרים בשמותיהם ברגע שהם מוצגים על המסך (ראו איור 1C); והשוואה בין מספרים. חוקרים השתמשו הרבה במשימת השוואת המִּסְפרים כדי לפענח כיצד ילדים מבינים מספרים. במהלך משימת השוואת המספרים מציגים לילדים שני מספרים על מסך מחשב (ראו איור 1D) והילדים צריכים לבחור את המספר הגדול יותר מבֵּין השניים במהירות המרבית האפשרית, בלי לבצע טעויות. ברגע שהם בוחרים את המספר הגדול יותר, הם לוחצים על הכפתור המתאים על המקלדת. כל הפעילויות השונות האלה יחד מספרות לנו עד כמה ילדים מבינים את המשמעות של מספרים. חוקרים השתמשו בכל הפעילויות כדי להסתכל על האופן שבּו ילדים עם דיסקלקוליה מוצאים את התשובות, בשונה מילדים באותו הגיל שאין להם דיסקלקוליה. נמצא שלילדים עם דיסקלקוליה יש קושי בשיום מספרים ובספירת נקודות, בהשוואה לילדים ללא דיסקלקוליה (ראו איורים 2B ,2A) [3]. נוסף על כך ילדים עם דיסקלקוליה הם איטיים יותר ומבצעים יותר טעויות בבחירת המספר הגדול יותר (המספר על המסך שמייצג כמות גדולה יותר של פריטים) במהלך ההשוואה (ראו איור 2C) [4 ,3]. המחקרים האלה מראים שאפילו במטלות מספריות פשוטות, ילדים עם דיסקלקוליה חווים קשיים רבים, אשר עשויים להוביל לכישורים חשבוניים ירודים.
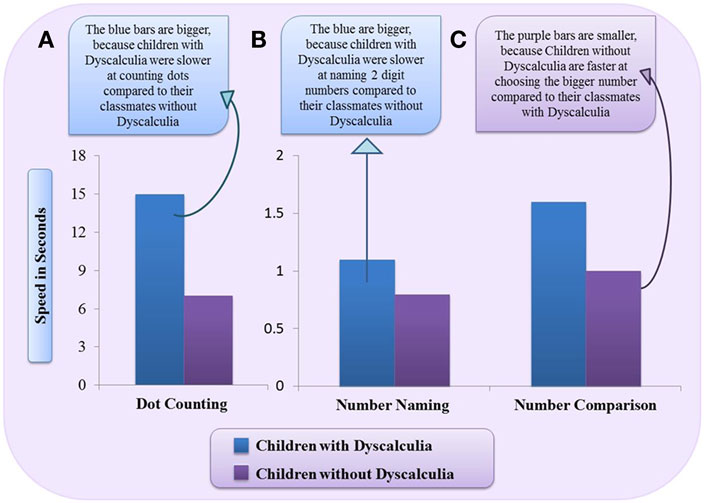
- איור 2 - ילדים עם דיסקלקוליה חווים קשיים גדולים עם מטלות מספריות שונות, יותר מאשר ילדים אחרים.
- העמודות הכחולות מייצגות את מהירות התגובה (עד כמה מהר הנבדק הצליח לענות על השאלה) עבור ילדים עם דיסקלקוליה, והעמודות הסגולות מייצגות את מהירויות התגובה של ילדים שאין להם דיסקלקוליה. A. במהלך משימת ספירת הנקודות, ילדים עם דיסקלקוליה הם איטיים יותר בספירת הנקודות כאשר ישנן יותר מ-10 נקודות. B. במהלך שיום מספרים, ילדים עם דיסקלקוליה הם איטיים יותר בשיום של מספרים דו-ספרתיים (מספרים ששווים ל-10 או גדולים ממנו). C. במשימת השוואת המספרים, ילדים עם דיסקלקוליה הם איטיים יותר בבחירת המספר הגדול יותר. התמונה הזו לקוּחה מממצאים שפורסמו במאמרם של Landerl ואחרים [3].
המוח של ילדים בעלי דיסקלקוליה חושב אחרת
בעוד שחוקרים מנסים לפענח כיצד ילדים עם דיסקלקוליה מבינים מספרים, הם גם מתחילים להסתכל על האופן שבּו מוחות של ילדים עם דיסקלקוליה עשויים להיות מאורגנים אחרת מהמוחות של ילדים שהתפתחותם המוחית היא רגילה.
דימוּת תהודה מגנטית תפקודי (fMRI) הוא אחד הכלים שבהם אנו משתמשים כדי לצלם את המוח בזמן שהילדים עובדים על פעילויות מספריות שונות. זה מאפשר לנו לראות אלה אזורים במוח עובדים בזמן שהילדים מבצעים חישובים מתמטיים או מעבדים מספרים בצורות שונות. במוח שלכם ישנוֹ אזור שמסייע לכם להשלים מטלות מספריות שונות, כמו למשל השוואה בין מספרים, והוא נקרא (Intraparietal Sulcus) IPS (איור 3) [5]. אולם המצב עשוי להיות שונה אצל ילדים עם דיסקלקוליה. לדוגמה, שני מחקרים שונים מצאו שילדים עם דיסקלקוליה לא השתמשו ב-IPS שלהם באותה המידה כמו חבריהם שאין להם דיסקלקוליה בעת בחירת המספר הגדול יותר במשימת השוואת המספרים [4, 6]. תוצאות אלה מצביעות על כך שהמוחות של ילדים עם דיסקלקוליה אינם עובדים טוב עם מספרים, ושאותם הילדים ככל הנראה משתמשים במוחותיהם בצורה שונה, אפילו כשמדובר במשימות פשוטות כמו השוואה בין מספרים. השוני הזה עשוי לעמוד בבסיס הקשיים בהבנת מספרים ובלמידת פעולות חשבוניות פשוטות. אף על פי כן עליכם להבין שלילדים עם דיסקלקוליה אין פגם במוח, אלא שמוחם פשוט פועל אחרת.
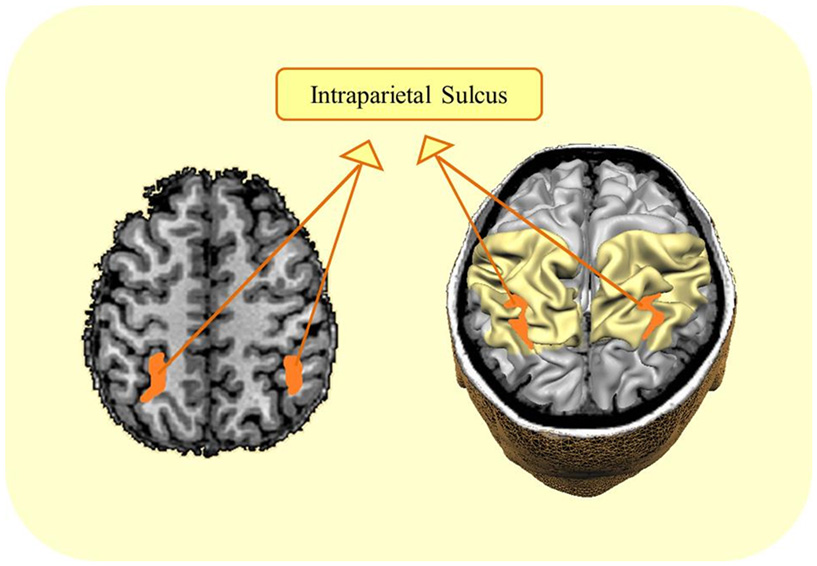
- איור 3 - אזור ה-IPS במוח מסייע לילדים להבין את המשמעות של מספרים.
- אזור זה ממוקם באחורי המוח, בתוך אזור אחר שנקרא הָאֻנָּה הקודקודית, אשר צבוע בצהוב בחלק הימני של התמונה. אזור ה-IPS מודגש בכתום בתמונה. התמונה המוחית שמשמאל היא תמונה של המוח שנרשמה באמצעות סורק fMRI. תמונת המוח שמימין היא ציור סכמטי של המוח.
איננו יודעים הרבה על האופן שבו מוח דיסקלקולי מתפתח. אולם אנו כן יודעים שילדים עם דיסקלקוליה חווים קושי בהבנה של מספרים. אם ילדים צעירים חווים קושי בהבנה של מספרים, אזי בהמשך לימודיהם בבית הספר הם יתקשו גם בלמידה של בעיות חשבוניות מורכבות יותר. בעת חישוב של 2+2, המוח של ילד עם דיסקלקוליה הוא איטי יותר בעיבוד המשמעות של המספר 2 וכתוצאה מכך לאותו הילד קשה יותר להגיע אל התשובה 4. חשוב שנבין יותר על האופן שבו מוח דיסקלקולי מתפקד, כך שנוכל לאתֵּר את אותם הילדים שסובלים מהלקות הזו. אנו מקווים שבעזרת מחקר וידע נוספים על דיסקלקוליה נוכל לפתח תוכניות עבור מורים, שבעזרתן המורים יוכלו לסייע לילדים שמתקשים בלימודי מתמטיקה. חשוב לנו שכֹּל הילדים יוכלו ללמוד מתמטיקה בהצלחה רבה ככל יכולתם. המחקר שֶׁסָּקרנו במאמר הזה מראה שזיהוי קשיים בשלב מוקדם עשוי לעזור למנוע בעיות נוספות בעתיד.
לבסוף, חשוב שתבינו כי קושי במתמטיקה אינו נובע בהכרח מדיסקלקוליה. חלק מהילדים תופסים מתמטיקה בתור מקצוע מפחיד אולם הם מסוגלים ללמוד אותה אם תינתן להם תמיכה מתאימה. ילדים עם דיסקלקוליה צריכים עזרה רבה יותר מאחרים כדי ללמוד מתמטיקה, ועליהם לקבל את העזרה הזו. נוסף על כך חשוב מאוד לדעת שאף על פי שנראה כי ילדים עם דיסקלקוליה משתמשים במוחם בצורה שונה מילדים אחרים, אין זה אומר שאינם יכולים לשנות את האופן שבּו המוח שלהם פועל (להרחבה בנושא זה קראו את המאמר הזה, שמסביר על שימוש בחינוך עבור פיתוח היכולות המנטליות). אנו יכולים לשנות את המוחות שלנו אם אנו משקיעים בכך מאמץ. אולם אנו גם צריכים להבין שלילדים עם קשיים כמו דיסקלקוליה קשה יותר לשנות את אופן חשיבתם, ולכן הם זקוקים לסיוע נוסף. כיום אנו יודעים הרבה פחות על דיסקלקוליה התפתחותית מאשר שאנו יודעים על הסיבות שבגינן ילדים חווים קשיים בקריאה (קשיים כאלה נקראים דיסלקציה התפתחותית). גם לא ברור עדיין כיצד שיטות לימוד שונות עשויות לעזור לילדים עם דיסקלקוליה. נעשו בעבר כמה ניסיונות להשתמש במשחקי מחשב כדי לעזור לילדים עם דיסקלקוליה התפתחותית, אולם כיום ידוע מעט מאוד על מידת ההצלחה של לימוד באמצעות אותם המשחקים [7]. במעבדה שלנו אנו מריצים מחקרים חדשים שמטרתם להבין טוב יותר את התופעה של דיסקלקוליה התפתחותית, ואנו מקווים להשתמש במחקר הזה יום אחד ולסייע בהקלה על חייהם של ילדים עם דיסקלקוליה התפתחותית, בתוך בית הספר ומחוץ לו [8].
הצהרת ניגוד אינטרסים
המחברים מצהירים כי המחקר נערך בהעדר כל קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.
מקורות
[1] ↑ Mazzocco, M. M., and Rasanen, P. 2013. Contributions of longitudinal studies evolving definition and knowledge of developmental dyscalculia. Trends Neurosci. Educ. 2:65–73. doi: 10.1016/j.tine.2013.05.001
[2] ↑ Geary, D. C. 1993. Mathematical disabilities: cognitive, neuropsychological, and genetic components. Psychol. Bull. 114:345–62. doi: 10.1037/0033-2909.114.2.345
[3] ↑ Landerl, K., Bevan, A., and Butterworth, B. 2004. Developmental dyscalculia and basic numerical capacities: a study of 8-9-year-old students. Cognition 93:99–125. doi: 10.1016/j.cognition.2003.11.004
[4] ↑ Price, G. R., Holloway, I., Rasanen, P., Manu, V., and Ansari, D. 2007. Impaired parietal magnitude processing in developmental dyscalculia. Curr. Biol. 17:R1042–3. doi: 10.1016/j.cub.2007.10.013
[5] ↑ Dehaene, S., Piazza, M., Pinel, P., and Cohen, L. 2003. Three parietal circuits for number processing. Cogn. Neuropsychol. 20:487–506. doi: 10.1080/02643290244000239
[6] ↑ Mussolin, C., De Volder, A., Grandin, C., Schlogel, X., Nassogne, M.-C., and Noel, M.-P. 2010. Neural correlates of symbolic number comparison in developmental dyscalculia. J. Cogn. Neurosci. 22:1–15. doi: 10.1162/jocn.2009.21237
[7] ↑ Kroeger, L. A., Brown, R. D., and O'Brien, B. A. 2012. Connection neuroscience, cognitive, and educational theories and research to practice: a review of mathematics intervention programs. Early Educ. Dev. 23:37–58. doi: 10.1080/10409289.2012.617289
[8] ↑ Butterworth, B. 2010. Foundational numerical capacities and the origins of dyscalculia. Trends Cogn. Sci. 14:534–541. doi: 10.1016/j.tics.2010.09.007