Abstract
Ever feel lost in math class or wonder why learning math even matters? Believe it or not, math is everywhere in the real world, from planning your day to building cool inventions. Researchers have found six recommendations to help students who are having difficulty learning math. There is even a whole area of research dedicated to improving how teachers teach math, so it is easier to learn and more useful. So, if you are ready to level up your math game, check out these research-backed strategies!
Why Do We Learn Math in School?
Have you ever heard someone in math class ask: “Why do we need to learn this?”… or maybe you have even asked it yourself! If students understand why they learn math in school, it can help them be engaged and motivated in the classroom.
Math is a valuable tool for everyday activities, like figuring out if you have enough money to buy candy, baking, interpreting data, and understanding statistics in news articles. Overall, learning math and engaging in math tasks support problem solving, identifying patterns, creative thinking, making sense of the world, and contributing in meaningful ways to society.
If you ever find yourself struggling with math, you are not alone! Many students encounter some challenges with learning math. An assessment given to students in the United States in 2024, called the National Assessment of Educational Progress, shared this finding: 61% of fourth graders performed below proficiency in math. While our article focuses mainly on U.S. math and research, students’ math performance is also a concern in other countries and is an important topic for all.
Does Research explore How to Teach Math to Students Who Are Struggling?
Because math is so important, many research studies have explored how to teach math to students in ways that are impactful, motivating, and engaging. This may be surprising to you, because research in education is perhaps not as well-known as research you learn about in biology and chemistry. When you hear the word “research”, you might think of lab coats and microscopes. But research in education can look like researchers and teachers working in the classroom with students, testing out strategies or a series of math lessons, and collecting and analyzing data to figure out if, how, and why the strategies help students learn (Figure 1).
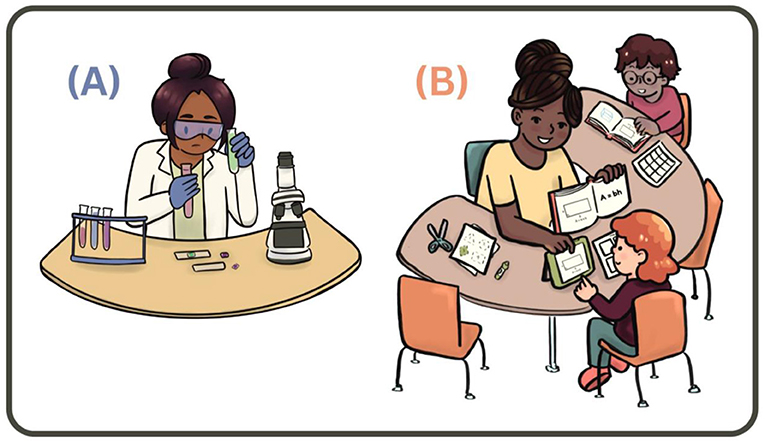
- Figure 1 - Research can look like both of these images! (A) Sometimes research is done in a lab.
- (B) Research in education focused on math learning can occur in schools and can look like researchers and/or teachers working with individual students, with small groups of students, or with a whole class. A common goal of studies about math learning is to explore if specific math strategies or series of math lessons, called interventions, are effective for boosting students’ math understanding (figure credit: Jennifer Hyles).
Some research studies focus on how to help students who are experiencing difficulties in math or have a math learning disability that impacts how they learn. These studies are important because researchers and teachers know that all students have the potential to be successful in math, even if they are currently struggling. Such research has uncovered six recommendations that boost learning for students who are struggling. A group of experts reviewed the research and wrote an excellent summary of the recommendations to share with teachers [1]. In this article, we share the recommendations with you—students!
Recommendation 1: Systematic Instruction
Teachers use systematic instruction to teach all types of learners in the math classroom. You can think of it as the foundation of your house. The foundation needs to be solid, or the house will be shaky. Maybe you have seen your teacher demonstrate how to solve a math problem, then you solved a similar problem together as a whole class or group, and then you did some problems independently to practice. This planned sequence of activities is part of systematic instruction. Your teacher may have asked you and your classmates a lot of questions, given you feedback on your work, or provided suggestions on how to do it better. All these examples are components of systematic instruction and are supported by research studies on how to teach math to students who are struggling [1].
Recommendation 2: Math Language
Do you ever feel like your teachers speak a different language when teaching math? Well, they kind of are: they are using mathematical language. When you use precise math words, like “sum” for addition or “factor” for multiplication, you are using math vocabulary that can explain your thinking clearly to others and make problem solving easier [1]. In math class, you may learn important new words for a unit while you learn about that topic. You might have pictures and graphic organizers in your class that help show important words and their meanings.
Researchers designed a type of study to test a series of word problem lessons, known as an intervention, among first-grade students. Some students were taught math vocabulary (example: “more than”) and some were not [2]. The research team discovered that learning about math language while learning strategies to solve word problems helped students be more successful with word problems.
Recommendation 3: Multiple Representations
When learning a new topic in math class, your teacher might show you the same concept in multiple ways or use multiple representations. There are three types of representations: concrete, pictorial, and abstract (Figure 2). Imagine that, when first learning how to multiply 5 by 3, your teacher gives each student a group of counting sticks. Your teacher asks you to put the sticks into five groups with three in each group. This shows that 5 groups of 3 (5 × 3) equals 15. Using physical objects to represent math is called a concrete representation. Then your teacher gives you a piece of paper and asks you to draw 5 groups with 3 circles in each group, to represent 5 × 3 differently. This drawing is a pictorial representation. And, throughout the lesson, your teacher uses the number representation of the multiplication problem “5 × 3”, which is the abstract representation.
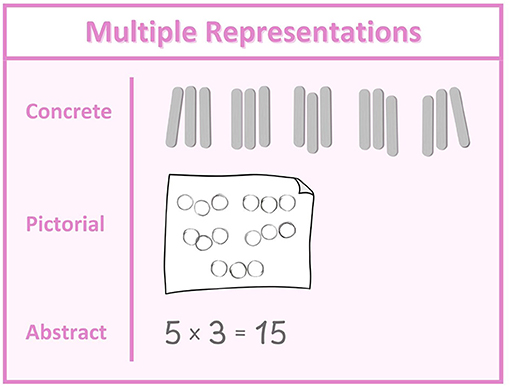
- Figure 2 - Three types of representations that can support mathematics learning are concrete, pictorial, and abstract.
- This figure shows representations of 5 × 3.
One team of researchers looked at 25 different studies that were all focused on supporting students who were struggling with math. The team found that using multiple representations was beneficial for improving the students’ math understanding [3].
Recommendation 4: Number Lines
The number line is special because it can do a lot of things to help students learn math. Horizontal number lines are used for learning about the size of numbers, calculating time, and displaying data. The number line can also be vertical, which can be helpful for understanding temperature. Sometimes students even imagine a number line in their heads to solve problems.
With fractions, for example, teachers can use a number line to help students understand how big or small fractions are or why rules for doing fraction arithmetic work the way they do [4]. Some important things to keep in mind are: a number line needs arrows on both “ends”, it is helpful to practice with different number lines (some number lines are 0 to 1 and others start with 0 and extend to 5, for example), and when you do number line activities, be sure to use precise math language as we mentioned already [4].
Recommendation 5: Word Problems
Word problems in math are like stories that show situations you could experience—and math is the tool to solve them. Research has shown that learning about different problem types is super helpful for solving word problems. Researchers used a strategy called RUN, which stands for “Read it”, “Underline the label”, and “Name the problem type” [2]. Here is an example: “There are five girls on the playground and three girls in the yard; how many girls are there?” Using the RUN strategy you first read the problem, then underline the label (girls), and name the problem type (total). Now solve to find the total: 5 + 3 = 8 girls.
Recommendation 6: Timed Math Activities
Imagine trying to solve a puzzle. If you already know how all the pieces fit, focusing on the bigger picture is easier than getting stuck on each piece. In math, the “pieces” can be things like adding and subtracting. It is important to practice solving basic math problems quickly, so you can become a more confident problem solver. One way to improve is by doing brief, timed exercises. The challenge is to answer math problems you already know how to do in 1- to 5-min periods and to fix any mistakes—otherwise, timed practice will not help.
Because timed activities are so important, they were used in all intervention groups in one research team’s study [2]. As a small part of each math lesson, students solved as many addition and subtraction flashcards as they could in a minute. Each time a student made a mistake, the teacher stopped them immediately and students were asked to find the correct answer. This helped the students remember the correct answers.
Bringing The Six Recommendations Together
Now that we have summarized each individual recommendation (Figure 3), let us talk about using the recommendations together. It is powerful when the recommendations are used in combination to help students achieve their math goals. Systematic instruction (Recommendation 1) and math language (Recommendation 2) can be used in every math lesson. And a single lesson about fractions, for example, could use many of the recommendations, including systematic instruction, math language, multiple representations, and number lines. If you are interested in seeing more hands-on math activities that use these recommendations, we encourage you to explore the practice guide that is freely available online to download here [1].

- Figure 3 - The six research-backed math recommendations summarized in this article: systematic instruction, math language, multiple representations, number lines, word problems, and timed activities.
Your Math Potential is Unlimited
We hope this article gives you ideas about how research is done in education, especially research on how students learn in math class. We summarized the six recommendations that researchers have studied and found work well for students who are struggling with math across all kinds of math topics.
But hold on! There is one more thing we want to share with you! It is important to know that you ARE a math person. In fact, everyone can be a math person! Sometimes math can be hard and that is okay, but if you keep practicing, you may surprise yourself with how much you learn. Every student has math potential!
Glossary
Math Learning Disability: ↑ This disability causes students to experience struggles with numbers and math concepts. It can make math challenging to learn, but there are strategies and recommendations that can help.
Systematic Instruction: ↑ Classroom materials and teaching that build students’ knowledge in a planned, gradual sequence to support their learning. It includes components such as immediate feedback and review of content.
Intervention: ↑ A specific program, series of lessons, or set of steps designed to help students who are struggling with a subject like math. Interventions are often one-on-one or in small groups.
Representations: ↑ Mathematical representations demonstrate/illustrate the value of numbers and relationships between numbers. Three representation types that support math learning are concrete (example: physical manipulatives like counting blocks), pictorial, and abstract.
Concrete Representation: ↑ A mathematical representation that uses physical objects (like buttons, blocks, or coins).
Pictorial Representation: ↑ A mathematical representation that uses pictures or drawings.
Abstract Representation: ↑ A mathematical representation that can use numbers, equations, operations, expressions, and symbols.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors would like to thank Dr. Lynn Fuchs for her insightful review of this manuscript, which significantly improved the quality of the work. They also thank Jennifer Hyles for the amazing Figure 1 illustrations. This work was supported by U.S. National Science Foundation (NSF) funding (NSF Award # 2237053). The authors also would like to thank Ryka for her thorough review of the manuscript. Ryka is a mathlete and a researcher. She is very interested in the distribution of prime numbers. Beyond maths, Ryka also loves computing, astronomy, and astrophysics.
References
[1] ↑ Fuchs, L. S., Newman-Gonchar, R., Schumacher, R., Dougherty, B., Bucka, N., Karp, K. S., et al. 2021. Assisting Students Struggling with Mathematics: Intervention in the Elementary Grades (WWC 2021006). Washington, DC: National Center for Education Evaluation and Regional Assistance (NCEE), Institute of Education Sciences, U.S. Department of Education. Available online at: https://ies.ed.gov/ncee/wwc/PracticeGuide/26 (Accessed February 10, 2025).
[2] ↑ Fuchs, L. S., Seethaler, P. M., Sterba, S. K., Craddock, C., Fuchs, D., Compton, D. L., et al. 2021. Closing the word-problem achievement gap in first grade: schema-based word-problem intervention with embedded language comprehension instruction. J. Educ. Psychol. 113:86–103. doi: 10.1037/edu0000467
[3] ↑ Jitendra, A. K., Nelson, G., Pulles, S. M., Kiss, A. J., and Houseworth, J. 2016. Is mathematical representation of problems an evidence-based strategy for students with mathematics difficulties? Except. Child. 83:8–25. doi: 10.1177/0014402915625062
[4] ↑ Rodrigues, J., Locke, S., L. Singell, E., and Mirielli, L. G. 2024. Teaching fraction magnitude using the number line. Interv. Sch. Clin. 59:165–72. doi: 10.1177/10534512231156885
