Abstract
When you think of creativity, what comes to your mind? Maybe you remember painting a picture, or you think of a special piece of music that you listened to or maybe even composed yourself. At some point, at least one of your teachers probably said something like “Let’s be creative!”. Then, it was up to you to decide how to work on a task. What makes creative projects truly special is that, in the end, each of your classmates creates something unique. But have you ever heard your math teacher encourage you to be creative? We guess that the answer is “No”. Why is it generally thought that creativity is so important in arts, but not in math? That is the question we are going to explore in this article. By taking a closer look at some examples of math tasks, we will describe four abilities that you need to be creative in math.
Being Creative = Thinking Outside the Box
First thing first, everyone can be creative! However, people differ in how often and how much they express their creativity in every aspect of their lives. So, you might enjoy being creative while singing, while someone else shows creativity when doing sports. We mostly love to get creative in math. But what does everyone have in common? What exactly does it mean to be creative?
Psychologists started dealing with this question about 70 years ago. One of the most famous creativity researchers was Joy Paul Guilford, who lived in the USA from 1897 to 1987. His groundbreaking findings still inspire researchers worldwide to conduct new studies on creativity. Guilford argued that creativity helps people when they do not know how to solve a problem. In those situations, they are challenged to think outside the box. This means to consider new perspectives and explore original strategies for solving a problem [1]. The Latin word for this process is creare which, in English, means to create or to make something. This is where the modern concept of creativity comes from.
Working Creatively on Math Tasks
People can get creative when drawing a picture, inventing a game, or trying out a new recipe. However, you can also get creative in science and math. In 1945, Jacques Hadamard was the first mathematician to point out the overlap between the (psychological concept) creativity and math [2]. What does this mean? Sometimes people might solve a math task differently from the way they learned or from what their teacher expects. Have you ever encountered math problems that you did not know how to solve? This can happen even if you have already learned many strategies and memorized important formulas—sometimes all of this knowledge is not enough to solve a math problem. This is where you must get creative and come up with something new. Let us look at a few math tasks and decide if we need to get creative when working on them.
Task 1: Solve 185+96
Do you immediately know the answer to this task, or is it challenging enough to get creative? Well, for us, the task was easy: We know that 96 is close to 100 and adding 100 to another number is simple. The next step is to subtract 4, so 185 + 96 = 185 + 100 - 4 = 281. We were not creative in solving this problem because we knew a trick. Such simple math tasks are not suitable for creativity.
Task 2: The school year is finally over! Four friends are so thrilled that they each want to give everyone a high five. How many times do the friends slap hands?
Can you be creative while working on this task? The solution to this task did not come to us right away. While we were pondering, suddenly an idea popped up: we could draw a sketch and use it to easily count the high fives (Figure 1).
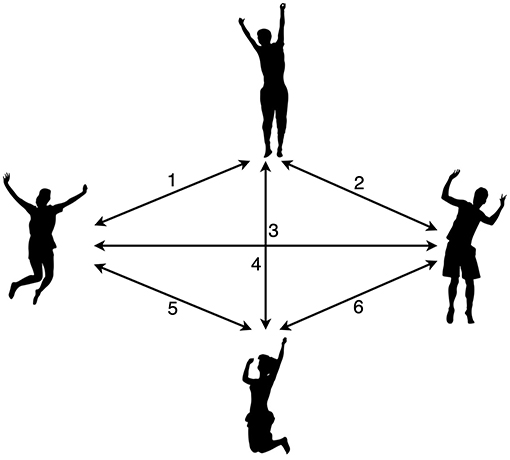
- Figure 1 - As one creative approach to this problem-solving task, we could draw a sketch like this one to figure out how many times four friends slap hands while giving high fives.
- Of course there are several other ways to figure out the answer.
By sketching out the problem, we arrived at a total of six high fives. How did you handle the task? You may have used a completely different approach. In any case, we all ended up being creative because we had to think outside the box, by finding our own way to tackle the task. So, problem-solving tasks like this are suitable for getting creative in math [2, 3].
Task 3: Find different math facts that contain the number 2, with the result of 48.
Can you be creative with this task? We would say so, even though this task is different from the previous problem-solving task. Because we did not have a set strategy for finding different arithmetic facts, we had to get creative (Figure 2). To begin with, we came up with the division task 96 ÷ 2 = 48 because we love dividing numbers. Next, we wanted to change the operation from division to addition, which is why we wrote 2 + 46 = 48. Then, we had the idea to use the commutative law, and ended up with 46 + 2 = 48. Finally, we decomposed the first summand into two numbers and therefore noted 40 + 6 + 2 = 48.

- Figure 2 - When working on this open task we need to be creative, because we do not have a set approach for finding different arithmetic facts.
How did you work on this task? You probably had many more ideas for collecting various facts. Such math tasks are called open tasks, and they are characterized by the need to find many different solutions. In doing so, everyone can be creative in his or her own way [3].
Four Creative Abilities
In the last section, we hope you learned a lot about the meaning of creativity. When people are creative, they think outside the box. This is something we all need in every aspect of our lives. In math, you can be creative when working on problem-solving tasks (like counting high fives), open tasks (like producing facts) or other math tasks that are new for you. However, what exactly do people do when they work creatively on math problems? What exactly does it mean to “think outside the box”?
To answer these questions, we can look at Guilford’s research once again [1]. He and many other researchers define creativity as the interaction of four abilities that everyone develops individually: fluency, flexibility, originality, and elaboration [4]. Let us look at these challenging terms more closely in relation to the task from Figure 2.
Fluency
When working on the task, we had various ideas that led to different facts with the number 2 and the result 48. In Figure 2, we wrote some ideas on notes (e.g., our favorite operation, change of operation, commutative law, and decomposition). You probably had some other exciting ideas. Sometimes these ideas just pop into your head. Other times, you may need to think a bit more deeply. Either way, everyone who solved this problem likely had a highly individual flow of ideas. This flow of ideas is what creativity researchers call fluency.
Flexibility
If we explore the ideas of different students, we uncover something interesting. It is possible to sort all the ideas so that similar or matching ideas are collected together in “boxes”. You could imagine there is a box labeled “Operation” that contains all ideas concerning the arithmetic operations used (e.g., favorite operation or change of operation). A second box could be named “Laws”, and it could represent all ideas in which mathematical laws were used (e.g., commutative law). Creativity researchers call these boxes types of ideas. For any math task, there is a unique variety of types of ideas. Every student will show a unique set of types of ideas. This is what we call flexibility. The more types of ideas you come up with, the more flexible you are.
Originality
If we take a closer look at the various ideas everyone came up with, some ideas may occur more frequently, while others are mentioned rarely. Guilford calls rare and mathematical ambitious ideas clever ideas. Creativity researchers say that people show originality when they present one of those “clever” ideas. So, the more rare or ambitious ideas you have, the more original you are. But beware: if many students work creatively on a math task, more diverse ideas will be generated. This makes it more challenging to come up with “clever” ideas and, consequently, to be original.
Elaboration
The various ideas you come up with start off in your mind. Until you write down and explain your ideas to a classmate or your math teacher, other people cannot fully understand them. So, it is important to describe your ideas in depth. Creativity researchers call the ability to explain your ideas elaboration. When you explain an idea aloud, you may come up with another (“clever”) idea right away. This means that your elaboration affects your fluency, flexibility, and originality. That is why elaboration is so important for being creative.
In the explanations of the four creative abilities, you probably noticed that all the abilities are related to each other [4]. These connections are illustrated in Figure 3. Your individual flow of ideas is the basis for your creativity (fluency). Within your various ideas, you show different types of ideas (flexibility) and “clever” ideas (originality). In addition, you should try to explain your ideas to others (elaboration).
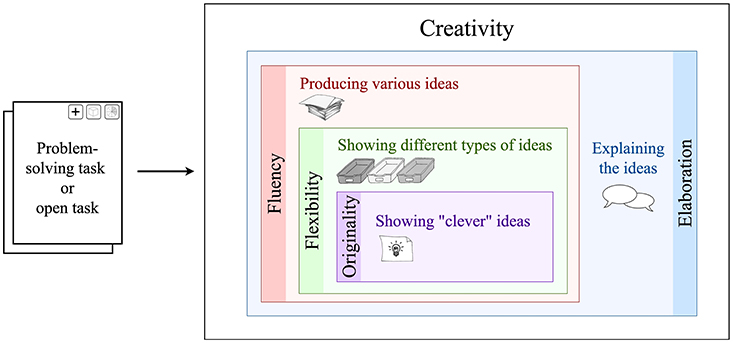
- Figure 3 - Working creatively on math problems involve four abilities: fluency, flexibility, originality, and elaboration.
- These creative abilities are all connected to each other.
Conclusion
The title of this article posed the question “Do we need creativity in math?”. Having now explored what creativity means in detail, we hope you can clearly see that the answer to this question is “Yes”. Just as in many other areas of life, everyone can be creative in math. Creativity means to think outside the box and you need it when you do not know how to solve a certain problem-solving task or open task. There are four closely related abilities that helps you being creative when working on math problems: fluency, flexibility, originality, and elaboration. At least for us, creativity is exactly why we love doing math so much. So let us all strive to be more creative in math!
Glossary
Psychologists: ↑ Professionals who study human learning and behavior.
Commutative Law: ↑ A computational law stating that you may swap the order of numbers in addition and multiplication facts, e.g., 3 + 1 = 1 + 3 and 2 ⋅ 4 = 4 ⋅ 2.
Summand: ↑ A number that is added to another number. The following applies: summand + summand = sum.
Open Tasks: ↑ Math problems that requires various solutions and solution methods.
Fluency: ↑ Producing various ideas when working creatively on problem-solving or open tasks.
Flexibility: ↑ Showing an individual set of types of ideas, i.e., different “boxes” with matching ideas that are generated when working creatively on problem-solving or open tasks.
Originality: ↑ Producing so-called “clever” ideas, i.e., rare or mathematical ambitious ideas, when working creatively on problem-solving or open tasks.
Elaboration: ↑ Explaining the various ideas verbally or in writing to another person.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
• llustration Credits
- Silhouettes of children (Figure 1): Illustration of OpenClipart-Vectors on Pixabay
- Sheet of paper (Figures 2, 3), Organizer boxes (Figure 3), and stack of paper (Figure 3): Publication with permission of SchoolCraft GmbH - www.worksheetcrafter.com.
References
[1] ↑ Guilford, J. P. 1968. Intelligence, Creativity, and Their Educational Implications, 1st Edn. San Diego, CA: Knapp.
[2] ↑ Hadamard, J. 1945. An Essay on the Psychology of Invention in the Mathematical Field. Princeton, NJ: Princeton University.
[3] ↑ Levenson, E., Swisa, R., and Tabach, M. 2018. Evaluating the potential of tasks to occasion mathematical creativity: definitions and measurements. Res. Math. Educ. 20:273–94. doi: 10.1080/14794802.2018.1450777
[4] ↑ Leikin, R., and Sriraman, B. (eds.). 2017. Creativity and Giftedness: Interdisciplinary Perspectives From Mathematics and Beyond. Cham: Springer International Publishing.
