Abstract
Have you ever wondered why the things you see around you look the way they do? A big part of my work as a computer graphics researcher is to answer this question, so that we can simulate real-world objects using computers. This work is important for creating movies and video games that are visually appealing to the audience. However, there are also many other applications of realistic computer graphics, such as training, product design, architecture, and others. In this article, I will tell you how we create realistic images of the world using computers, and how my work improved the way we simulate skin and hair in virtual characters. It will give you a new perspective on the magic and beauty of the visual scenery that we experience in our everyday lives and on the computer-generated images and movies that imitate these natural scenes.
Professor Pat Hanrahan won the Turing Prize in 2019, jointly with Dr. Edwin Catmull, for fundamental contributions to 3D computer graphics and the impact of computer-generated imagery (CGI) in filmmaking and other applications.
The World Around Us
What do you see when you look out of your window? I see some oak trees with beautiful leaf canopies. When it is sunny, the leaves seem to be glowing with glorious light. Because I have worked for so many years in computer graphics, I look at our everyday surroundings with an inquisitive, observing mind. When I see a beautiful landscape, I notice subtle variations in lighting of natural objects, such as that on the leaves outside my window, I wonder: what makes it so visually interesting and beautiful? How exactly do the leaves scatter the sunlight that hits them before it reaches my eyes? And what would be the best way to imitate this using a computer so that the leaves on my computer screen will also look beautiful as they do in nature?
If you think about it, everything that we see in the world—from trees to people to clothes—is made up of complex shapes and materials. To describe the composition of a visual scene, we must describe all the geometric shapes that make up the objects within that scene, as well as the materials they are made of. If we look at a human, for example, we see the skin, the face, the hair, the clothes—all made of materials with unique properties. There are also several kinds of light sources—the Sun, a neon light, or a spotlight, for example—and each source creates a unique pattern of lighting. Finally, the observed scene is perceived by the viewer (or recorded by the camera) from a certain point of view. A close look at any scene reveals a huge variety of elements working together to eventually create the image we see. We usually take what we see for granted in our daily lives, but when we must create a realistic image of the world using a computer, we begin to appreciate how interesting and intricate our visual reality is and how challenging it is to represent it convincingly in the computer.
Simulating the World Using Computers
In my early career, I worked at Pixar—a studio well-known now for their animated stories. Pixar wanted to make special effects in movies more convincing by combining computer-generated material with photographs taken of live action. To seamlessly combine the computer-generated parts with photographs, the computer-generated images had to be photorealistic, meaning indistinguishable from real-world photos (Figure 1). This required creating 3D pictures from descriptions of the elements in a scene. This was the first stage in the process called rendering—simulating the world using a computer (to learn more about rendering, see this video) [1]. Eventually, we realized that rendering could be used not only for special effects, but for creating entire movies only in the computer without having to film them in nature. I was fascinated by the challenge of creating a realistic virtual world, and for the last 30–40 years I have been making rendering better and better.

- Figure 1 - The road to point Reyes.
- This image, produced in 1983 by Lucasfilm (which later became Pixar), is an example of a high-resolution photorealistic image created using a computer. It marked an important milestone toward the creation of computer-generated digital films (Image source: http://www.calgran.net/upf/recursos/ima_dig/_2_/estampes/d3_1.html).
How does rendering work? First, artists, designers, and animators provide us with 3D descriptions (in drawings or in text) of the world we want to simulate. These descriptions are saved within computer files. Once we have a complete description of a specific scene, we must create a computer model of it to eventually convert the description files into actual images like the JPEG files you might be familiar with. The simplest way to model complex shapes with a computer is by using polygons, such as triangles and squares (Figure 2). We break all the complex shapes in a scene down into very small triangles, normally billions of polygons per image. Then, one of the biggest challenges for realistic rendering is to correctly simulate the lighting. The simplest way to model light in a computer-simulated world is to assume that light rays move in straight lines. To model light correctly, we use a technique called ray tracing, in which we follow the paths of simulated light rays in our virtual scene, to figure out what the lighting of this image should look like.
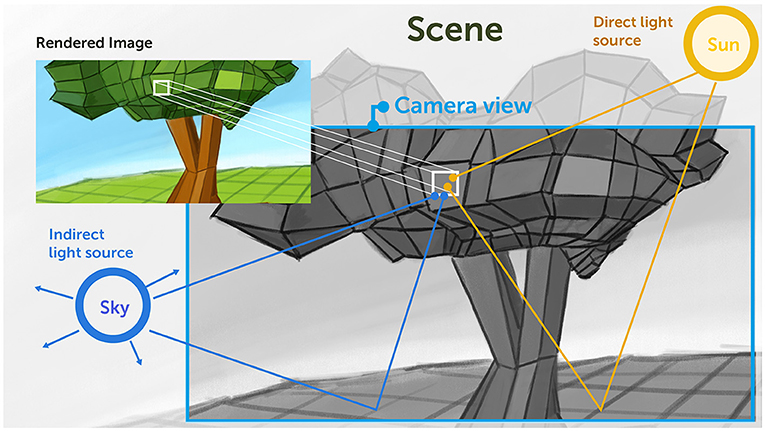
- Figure 2 - Simulating light to make images realistic.
- A complex scene is represented in the computer by a set (of often millions or billions) of small polygons. To determine the brightness and color of each pixel in the rendered image, we trace the paths of rays emanating from the light source and simulate how they are reflected from the surfaces they hit. We account for direct lighting, where the light is reflected directly to the eye or camera. The more challenging problem is indirect lighting, where light from the sun illuminates other objects which scatter light which eventually reaches the eye. An example is skylighting where light from the sun is reflected from the clouds and the atmosphere, or indirect lighting from light fixtures of the walls in a building.
Every direct light source in a scene, like the Sun or a light bulb, emits light rays. These rays travel in space until they hit the surface of some object and get scattered. Every material scatters light in a unique way, depending on the specific properties of its surface (for example, how smooth and transparent it is). Much of our work as computer graphics researchers is focused on simulating how different materials (say a stone, cloth or the skin) scatter light. For every material we eventually want to find a mathematical function that describes how that material scatters light. This mathematical function is called the scattering function of the material.
One way to model the scattering function of a material is to represent the material’s surface as if it is composed of many small mirrors pointing in various directions (Figure 3B). When light rays hit a perfect mirror, they are reflected at an angle that is equal to the angle at which they hit the mirror (Figure 3A). Modeling the scattering function of a material as a random distribution of mirrors on its surface can work well for some materials, but many natural materials require more sophisticated models. We can determine the scattering functions of complex materials by direct measurements of light scattered from these materials. To do this, we shine light on the material, and measure the light scattered off of it in various directions. We can store the reflection in tables or arrays and use this information to model this specific material in the computer. We can also fit physical models to these measurements.
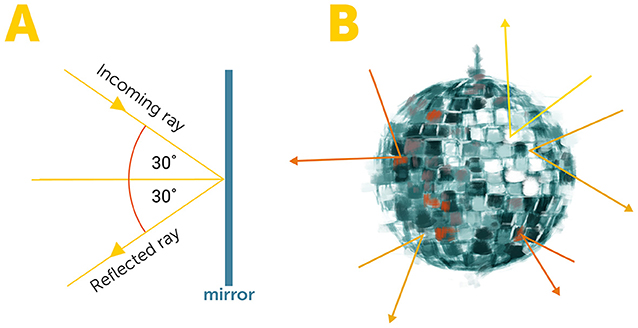
- Figure 3 - Modeling materials using mirrors.
- (A) In a perfect mirror, light rays are reflected such that the angle at which the rays hit the mirror is equal to the angle at which they leave the mirror. (B) A simple way to approximate the scattering function of a material is to model its surface as a collection of perfect mirrors, each scattering the light in a known way. This works well for some materials, while others require a more complex model.
How Does Your Skin Look So Good?
One of the most interesting problems I worked on was how to realistically model skin. In early movies that used rendering, skin looked quite unhealthy and artificial. No wonder, as it was essentially modeled like plastic! Healthy skin has a special glow to it that makes it look alive. There were no physics books explaining why skin looks this way, but luckily, I found two sources of information to help me crack this riddle. The first was work modeling of the atmospheres of planets (like Venus, Mars, or Jupiter), to explain why planets look the way they do. Planets often have a special glow around them, like skin does—see for example this image of Jupiter. These models of the planet’s atmospheres contained a solid core (the planet) surrounded by a thin layer of gases.
The second clue came from an art history book in the library at Princeton University, describing how the great painter Rembrandt painted skin, which look highly realistic in his paintings. He would layer pigments and oils on top of each other to create the skin’s lively glow (to learn more about how Rembrandt painted skin, see here). Rembrandt was not familiar with the structure of the skin, but he somehow intuitively captured the fact that skin has several layers. Pictures explaining his painting technique show light rays going into the layers of the skin and eventually being reflected back out from the top layer. Using these two clues, I developed the first mathematical model of the scattering function of the skin [2]. This model was based on a process called subsurface reflection, in which light enters through the surface of the skin, hits the skin’s internal, subsurface layers, gets scattered, and then comes back out (Figure 4). I wanted my first model to be as simple as possible, so I assumed that incoming light that scattered underneath the skin’s surface comes out from the same point where it entered. This model was a fairly good simulation of skin, so I knew this was the right approach.
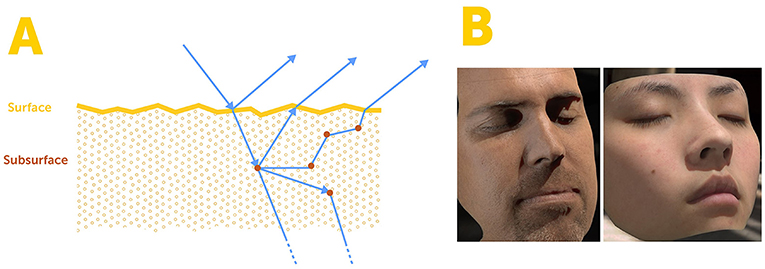
- Figure 4 - Subsurface reflection.
- (A) The skin is made of multiple layers. When light hits the skin, some of the light is reflected from the skin’s surface and some of it enters the skin’s subsurface layers. There, the light gets scattered in various directions and some of it comes back out in locations different from where it went in. This property was incorporated by the mathematical model we developed which provided a realistic simulation of skin in computer. (B) An example of realistic skin rendering. Adapted from d’Eon et al. [3].
However, my simple model made skin look bumpy, so I eventually developed a more complicated skin model, in which the light comes out of the skin at a different point from where it entered. That made the math behind the model more complicated, but it was worth it—the skin finally looked smooth! The reason the skin initially looked bumpy was that, if a small area has one lit side and one dark side, it will look like a bump. But, if the light that enters from the lit side is scattered inside the skin and comes out on the dark side, the dark side also gets lit. In other words, the subsurface reflection spreads out the light in a way that makes the skin look smooth.
I also had an interesting journey trying to model hair. Early on, hair also looked unrealistic in renderings. It turned out that modeling hair as colored, transparent cylinders works very well [4]. Humans have about 100,000 hairs on their heads and, in current movies, each hair is individually simulated using a cylindrical model. Of course there are different kinds of hair, so human hair is modeled differently than animal fur, for example. It took time, but computer graphics designers eventually realized how to model each type of hair—now, simulated hair looks very good.
Math Power in Computer Graphics
Simulating light requires math because we must find and use the correct scattering functions to track the way light rays move in virtual scenes. But there is another important use for math in computer graphics simulations. In the real world, a practically infinite number of light rays enters every scene. Each ray hits objects and gets scattered an infinite number of times before the light reaches the observer. To realistically simulate light in a virtual scene, we must sum up all the paths that light could travel to arrive at a certain point, to understand how much light we have at that point. We cannot analytically perform this summation. So, we must take a finite number of samples that accurately represents all the possibilities. How can we figure out how many samples will give us the best estimate of lighting? To do this, we use a mathematical method that was originally used to predict the behavior of randomly bouncing particles, called the Monte Carlo simulation [5].
Today, every pixel in a simulated movie image has about 1,000 light rays coming into it and randomly bouncing around. There are billions of pixels in every image, so we must track an extraordinarily large number of rays for every frame within every scene. This requires a lot of computations and is very expensive. The fastest computers in the world are used to perform the computations for computer-generated movies and computer games. In a typical movie, about 30 h of computing by the fastest computers are needed to compute a single film image. This can mean that some movies need up to one million hours of computing time! That is a lot of time, but it would be orders of magnitude more if we had not developed the mathematical tools that significantly decreased the number of calculations needed.
The next time you watch a computer-generated scene in a movie, I hope that you will have a new appreciation for the amount of research and computing resources that went into making it! Our everyday world becomes quite magical when we look at it from a computer scientist’s perspective. I invite you to learn to see the beauty of the world through careful observation, with curiosity about why things look the way they do.
Glossary
Computer Graphics: ↑ Generation of digital images using computers.
Rendering: ↑ The process of taking a description of a 3D scene and converting it into a computer image.
Computer Model: ↑ Representation, using the computer, of real-life situations and processes.
Ray Tracing: ↑ A method used in rendering to figure out the lighting of a scene by simulating the behavior of light.
Scattering Function: ↑ A mathematical description of how a specific material scatters the light that hits it.
Subsurface Reflection: ↑ A type of light scattering in which light enters a material at one point, scatters underneath its surface, and exits at another point.
Monte Carlo Simulation: ↑ A mathematical method that uses random sampling to calculate the outcome of an uncertain event. It is used in computer graphics to simulate the lighting in digital scenes.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
I wish to thank Or Raphael for conducting the interview which served as the basis for this paper, and for co-authoring the paper, Alex Bernstein for providing the figures, and Susan Debad for copyediting the manuscript.
Additional Materials
References
[1] ↑ Pharr, M., Jakob, W., and Humphreys, G. 2016. Physically Based Rendering: From Theory to Implementation. Cambridge, MA: Morgan Kaufmann.
[2] ↑ Hanrahan, P., and Krueger, W. 1993. “Reflection from layered surfaces due to subsurface scattering,” in Proceedings of the 20th Annual Conference on Computer Graphics and Interactive Techniques (New York, NY). p. 165–74.
[3] ↑ d'Eon, E., Luebke, D., and Enderton, E. 2007. “Efficient rendering of human skin,” in Proceedings of the 18th Eurographics Conference on Rendering Techniques (Goslar). p. 147–57. doi: 10.5555/2383847.2383869
[4] ↑ Marschner, S. R., Jensen, H. W., Cammarano, M., Worley, S., and Hanrahan, P. 2003. Light scattering from human hair fibers. ACM Transact. Graph. 22, 780–91.
[5] ↑ Harrison, R. L. 2010. “Introduction to monte carlo simulation,” in AIP Conference Proceedings, Vol. 1204 (Bratislava: American Institute of Physics). 17–21.
