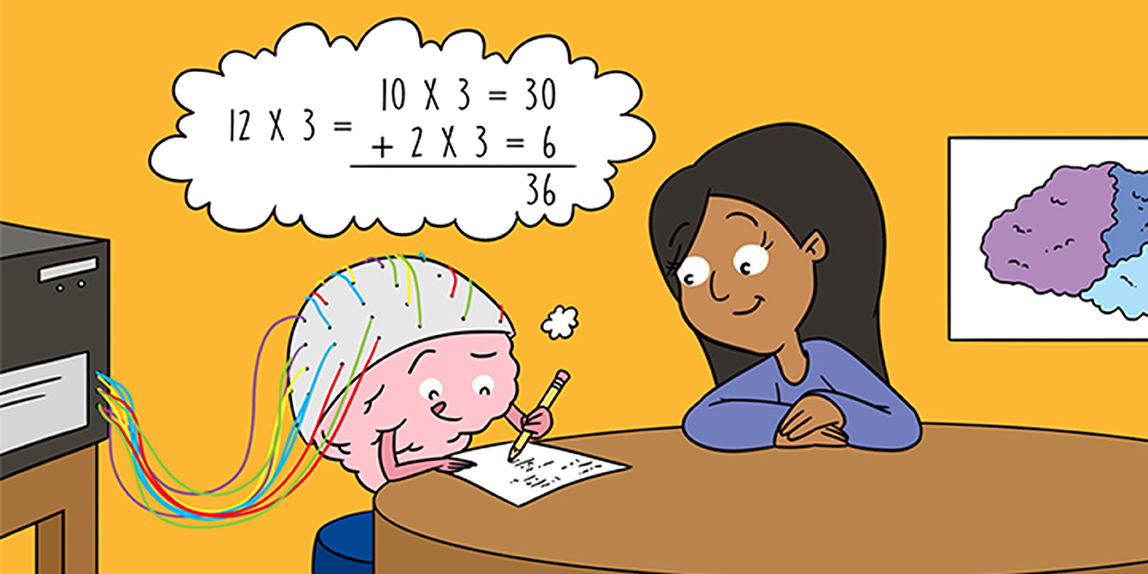Abstract
How much is 2 × 4? Sounds like an easy question, but have you ever thought about how you solve that problem? In this article you will learn about two different strategies that we use to solve arithmetic problems. You will also get to know the different brain areas—like the intraparietal sulcus—that work together when you use these different strategies. Which strategy and which brain regions you use changes over time as you get more familiar with arithmetic. This transition is especially visible in the way brain areas work and communicate with one another—some areas become more active, while others become less active. After reading this article, you will know more about the techniques we use to solve arithmetic problems and the brain areas needed to find the answers for your next math homework assignment.
Introduction
Because math is one of the most important skills to master, understanding how arithmetic problems are solved can have a very big impact. Not only do you need math every day at school, but also as a grown-up. If you want to become a programmer, an engineer, or a scientist, you will deal with numbers on a daily basis. Because math is important in almost every job, people who are not good at math sometimes have a hard time finding a job. Some of them might even suffer from something called developmental dyscalculia. Therefore, understanding what happens in the brain when you calculate can be very helpful for kids who struggle with math. Understanding the reason for these difficulties enables teachers to structure their lessons in a way that allows children to learn more easily. And of course, just being curious about how things work is always reason enough to conduct an experiment!
Are There Different Ways to Solve an Arithmetic Problem?
To study arithmetic, children and adults are usually asked to solve arithmetic problems as fast and accurately as they can. The problems are usually presented on a computer screen, one after the other (see Figure 1). Once the participant provides an answer, the next problem appears. To study the different strategies that we use during arithmetic, scientists usually use a mix of different arithmetic operations of varying difficulty.

- Figure 1 - Example setup for a study investigating arithmetic problem solving.
- Participants are presented with an arithmetic problem on a computer screen. Once the answer is given, a new problem appears. For each problem, researchers record the time it took to solve the problem (speed) and if the answer was correct (accuracy).
Using these methods, scientists found that arithmetic problems can be divided into two categories: small and large problems. Small problems are solved very quickly, and participants make fewer errors when solving these problems. A good example would be “2 × 4.” Large problems are usually a bit harder to solve. Participants take longer to solve these problems and also make more errors. A good example would be “12 × 3.” Scientists sometimes disagree on where to draw the line between small and large problems. How hard it is to solve a problem depends on your age and ability. However, speed and error differences between small and large problems suggest that we use two main strategies to solve them [2].
The first strategy, calculating the answer, is often used with large problems. It is called procedural strategy, because coming up with the answer involves multiple steps—or multiple procedures. For example, to solve “12 × 3” you might split the problem into two easier ones like “10 × 3 = 30” and “2 × 3 = 6.” Afterwards, you can add up the results to get the answer “36.” But adding extra steps has its downsides. It takes more time and each step also increases the chance of making errors. You do not, however, use the same strategy to solve the same problem forever. After solving it multiple times, the correct answer will 1 day just pop into your head. This shows that the way you solve this problem has changed.
Now you are using the second strategy: knowing the answer by heart—often called fact retrieval. By practicing the same problem multiple times, you stored its answer in your long-term memory. The switch from using procedural strategies to using fact retrieval is an important step during the development of arithmetic abilities [3]. Instead of calculating the answer, you are now able to remember it. Additionally, by becoming better at solving easier problems, you are also becoming better at solving more difficult problems. To better understand these changes, we need to look inside our brain while it solves arithmetic problems. To do so, scientists use different tools, such as electroencephalography (EEG) and functional magnetic resonance imaging (fMRI, see Figure 2).

- Figure 2 - Children taking part in one of our functional Magnetic Resonance Imaging (fMRI, left) and Electroencephalography (EEG, right) studies.
- These two tools let scientists study the brain while it is working.
Which Brain Areas Are Involved in Solving Arithmetic Problems?
Trying to understand how the brain works can sometimes feel like solving a complicated puzzle. Similar to the way a puzzle is made up of different pieces, your brain is made up of different brain areas (see Figure 3). Understanding each brain area’s function will give you a clearer picture of how it fits into the puzzle.
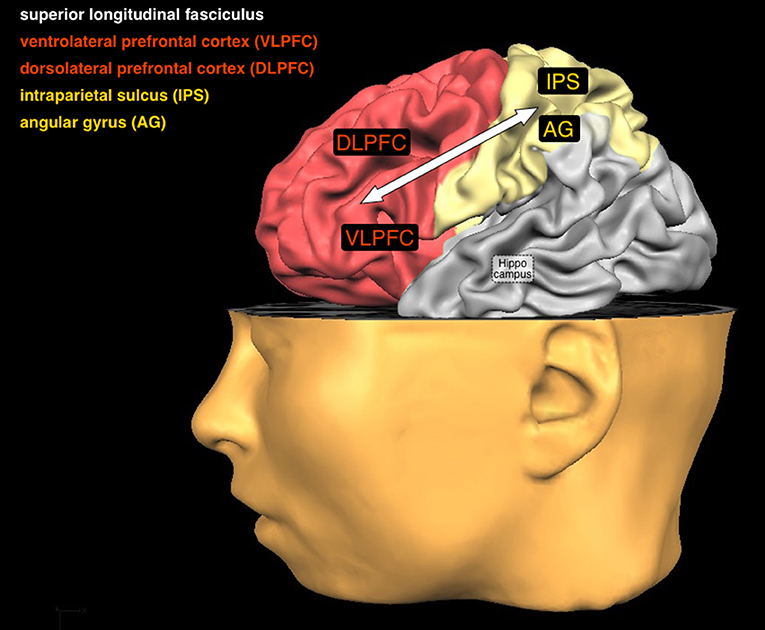
- Figure 3 - In this figure you can see a number of brain areas and one connection that are important for arithmetic.
- Two of them are in the frontal cortex (red) and two are in the parietal cortex (yellow). How they work together when you calculate depends on your age and your ability. Another important brain area, the hippocampus, is in the very center of your brain and therefore hidden from view.
The first piece of the puzzle is the intraparietal sulcus. It is located in the parietal cortex and is responsible for understanding the meaning of numbers [4]. The first step when solving an arithmetic problem is to understand a number’s magnitude. For example, you have to know that “4 dogs” are more than “2 dogs.” You also need to understand the order of numbers (i.e., “1” comes before “2,” that “2” comes before “3,” and so on). While calculating, you use your understanding of magnitude and order to find the correct solution.
The next pieces of the puzzle involve three brain areas in the frontal cortex. The ventrolateral prefrontal cortex works with regions in the parietal cortex to blend out distractions, such as daydreaming about your next bike ride with your friends. The dorsolateral prefrontal cortex is needed to manipulate numbers, like splitting up a large problem into easier steps. The inferior frontal gyrus has been found to play an important role in ignoring similar but incorrect answers [5].
The last pieces in our puzzle are the hippocampus and the angular gyrus. The hippocampus is located deep inside your brain. It plays an important role in storing arithmetic facts [6]. The hippocampus is the “save” button of your brain. When it comes to math, it works with the frontal cortex to help you store the answers of arithmetic problems as arithmetic facts in your long-term memory. The angular gyrus is then involved in finding these facts when you solve arithmetic problems.
How Does Solving Arithmetic Problems Change As You Get Older?
Have you and your friends ever worked on a challenging puzzle together? If so, you probably worked together to solve it. Your brain works in a similar way. Different brain regions work together when solving a problem. The last piece in our puzzle is understanding how these brain areas work together when you calculate. As you now know, the way you solve arithmetic problems changes as you get older. Instead of mostly using procedural strategies to solve arithmetic problems, you start using fact retrieval more often. But this is not the only thing that changes. Scientists found that during this process the way the different brain areas work together changes as well. For example, while you are young, the frontal cortex has a very important role. It manages your working memory and attention, because the way you solve arithmetic problems involves multiple steps (procedural strategies). As you get older and start to use fact retrieval, the role of your frontal cortex changes. When you look at the frontal cortex using fMRI or EEG, you can see that it becomes less active as you get older. It is still involved in the process of finding the right answer, but it does not have to work as hard as before. Maybe you have experienced something similar when cooperating with your friends. At first, one of you might have had to keep an eye on everyone’s progress and give instructions what to do next (similar to the frontal cortex). After you have successfully solved a few puzzles together, you will be able to work together without needing someone to always check on the progress. The role of the hippocampus changes too. During fact retrieval it is more active in young children than in adults [7]. This is because when you are young, the hippocampus is still working hard to save the answers to arithmetic problems to your long-term memory. As you get older your hippocampus has to work less and less, because you come across fewer new answers that have to be saved.
All of the brain areas work together by communicating with one another. This communication happens over a wide network of pathways (called white matter) that connect all brain areas. These networks are similar to the way in which roads connect different cities. One of these roads in the brain is called the superior longitudinal fasciculus. This road connects the prefrontal cortex with the parietal cortex (where the IPS is located) [8]. Because different brain regions are involved in the process of solving arithmetic problems at certain points in your life, the connections between these regions change as well. Scientists are still trying to fully understand how and why these connections change as you get older. That means, even though we already know a lot about how you solve arithmetic problems, we still need to do more research to complete the puzzle of the calculating brain.
Summary
Even if it sounds like a simple process at first, solving an arithmetic problem actually involves many steps. Not only that, but as you get older you use different strategies to solve them. Almost every part involved in your brain changes. At first, many brain areas work together to solve an arithmetic problem. Some parts keep you focused on the task, others keep track and memorize the results of your calculations. The hippocampus saves the correct result in your long-term memory. As you get older, you only need a few specialized brain areas to solve the same problem. Your brain now works very efficiently. Next time you do your math homework, take a minute to think of all the different brain areas that are involved!
Glossary
Developmental Dyscalculia: ↑ Is a difficulty in learning or understanding arithmetic. For a good overview look at the Young Minds article; When your brain cannot do 2 + 2: a case of developmental dyscalculia [1].
Electroence-phalography (EEG): ↑ A neuroscientific tool to measure the electrical signals a brain produces. This method can tell us with high accuracy at what time point brain areas are performing a specific task.
Functional Magnetic Resonance Imaging (fMRI): ↑ A tool to measure oxygen differences in the brain. Because active areas need more oxygen during a task, we can tell with high accuracy which parts are doing the job.
Brain Areas: ↑ The brain can be divided into four major parts: the frontal cortex, the parietal cortex, the temporal cortex, and the occipital cortex. Each cortex contains brain areas with unique functions.
Working Memory: ↑ A crucial function of your brain. Similar to the working memory of a computer, it stores information in your mind in order to work with it when you need it.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We would like to wholeheartedly thank those who assisted in the translation of the articles in this Collection to make them more accessible to kids outside English-speaking countries, and for the Jacobs Foundation for providing the funds necessary to translate the articles. For this article, we would especially like to thank Nienke van Atteveldt and Sabine Peters for the Dutch translation.
References
[1] ↑ Bugden, S., and Ansari, D. 2014. When your brain cannot do 2 + 2: a case of developmental dyscalculia. Front. Young Minds 2:8. doi: 10.3389/frym.2014.00008
[2] ↑ Siegler, R. S. 1996. Emerging Minds: The Process of Change in Children’s Thinking. New York, NY: Oxford University Press. doi: 10.5860/choice.34-5984
[3] ↑ De Smedt, B. 2016. “Individual differences in arithmetic fact retrieval,” in Mathematical Cognition and Learning, eds D. B. Berch, D. C. Geary, and K. M. Koepke (San Diego, CA: Academic Press). p. 219–43. doi: 10.1016/B978-0-12-801871-2.00009-5
[4] ↑ Vogel, S. E., Goffin, C., and Ansari, D. 2015. Developmental specialization of the left parietal cortex for the semantic representation of Arabic numerals: an fMR-adaptation study. Dev. Cogn. Neurosci. 12, 61–73. doi: 10.1016/j.dcn.2014.12.001
[5] ↑ De Visscher, A., Vogel, S. E., Reishofer, G., Hassler, E., Koschutnig, K., De Smedt, B., et al. 2018. Interference and problem size effect in multiplication fact solving: individual differences in brain activations and arithmetic performance. Neuroimage 15:718–27. doi: 10.1016/j.neuroimage.2018.01.060
[6] ↑ Qin, S., Cho, S., Chen, T., Rosenberg-Lee, M., Geary, D. C., and Menon, V. 2014. Hippocampal-neocortical functional reorganization underlies children’s cognitive development. Nat. Neurosci. 17:1263–9. doi: 10.1038/nn.3788
[7] ↑ Cho, S., Metcalfe, A. W. S., Young, C. B., Ryali, S., Geary, D. C., and Menon, V. 2012. Hippocampal–prefrontal engagement and dynamic causal interactions in the maturation of children’s fact retrieval. J. Cogn. Neurosci. 24:1849–66. doi: 10.1162/jocn_a_00246
[8] ↑ Matejko, A. A., and Ansari, D. 2015. Drawing connections between white matter and numerical and mathematical cognition: a literature review. Neurosci. Biobehav. Rev. 1:35–52. doi: 10.1016/j.neubiorev.2014.11.006