תַקצִיר
תהיתם אי פעם מדוע הדברים שאתם רואים סביבכם נראים דווקא כך? מציאת תשובה לשאלה הזו היא חלק מרכזי בעבודה שלי כחוקר גרפיקה ממוחשבת, כך שנוכל להשתמש במחשבים כדי לדמות עצמים מהעולם האמיתי. עבודה זו חשובה מאוד ביצירת סרטים ומשחקי וידאו, כדי שיהיו מושכים מבחינה חזותית. עם זאת, גרפיקה ממוחשבת מציאותית מיושמת בתחומים רבים אחרים, כגון הדרכות, עיצוב מוצר, ארכיטקטורה ועוד. במאמר זה, אספר לכם כיצד אנחנו יוצרים דימויים מציאותיים של העולם באמצעות מחשבים, וכיצד העבודה שלי שיפרה את הדרך שבה מדמים עור ושיער עבור דמויות וירטואליות. המאמר יאפשר לכם להביט מזווית חדשה על הקסם והיופי של המראות היום־יומיים סביבנו, ועל הדימויים והסרטים שנוצרו באמצעות מחשב, המחקים את המראות הטבעיים האלו.
פרופ’ פָּט הָנְרַהָן זכה בפרס טְיוּרִינְג ב־2019 יחד עם ד"ר אֶדְוִוין קָטְמוֹל, על תרומות יסוד לתחום הגרפיקה הממוחשבת בתלת־ממד, ועל השפעת דימויים הנוצרים במחשב (CGI – Computer-Generated Imagery) על תעשיית הסרטים ועל יישומים אחרים.
העולם סביבנו
מה אתם רואים כשאתם מסתכלים מבעד לחלון? אני רואה כמה עצי אלון בעלי צמרות יפהפיות. בשמש, העלים נראים מבהיקים באור זוהר. כיוון שעבדתי שנים רבות בתחום הגרפיקה הממוחשבת, אני בוחן את הסביבה היום־יומית בעיניים סקרניות. כשאני מביט על נוף יפה, אני מבחין בסוגי התאורה העדינים והשונים בטבע, כמו האור על העלים שנראים מהחלון שלי, ותוהה: מה הופך אותם למעניינים ויפים כל כך מבחינה חזותית? כיצד בדיוק מפזרים העלים את אור השמש שפוגע בהם לפני שהוא מגיע לעיניי? ומה תהיה הדרך הטובה ביותר לחקות זאת באמצעות מחשב, כדי שגם העלים על מסך המחשב שלי ייראו יפים כמו בטבע?
כשחושבים על זה, כל מה שאנו רואים בעולם – מעֵצים ואנשים, ועד בגדים – עשוי מצורות ומחומרים מורכבים. כדי לתאר ממה מורכבת סצנה חזותית, עלינו לתאר את כל הצורות הגיאומטריות המרכיבות את העצמים בסצנה, וכן את החומרים שמהם הם עשויים. כאשר בוחנים אנשים, לדוגמה, רואים את העור שלהם, את הפנים, השיער והבגדים – וכל אחד מהם עשוי מחומרים בעלי תכונות ייחודיות. יש גם סוגים שונים של מקורות אור – למשל שמש, נורות ניאון או זרקורים, וכל אחד מהם יוצר דפוס תאורה ייחודי. כמו כן, הצופים (או המצלמה) תופסים כל סצנה מזווית מסוימת. כשבוחנים כל סצנה לעומק מגלים מגוון עצום של אלמנטים המשתלבים זה בזה ויוצרים בסופו של דבר את התמונה שאנחנו רואים. בדרך כלל הדברים שאנחנו רואים בחיי היום־יום מובנים לנו מאליהם, אך רק כאשר עלינו ליצור תמונה מציאותית של העולם באמצעות מחשב, אנחנו מתחילים להבין עד כמה מעניינת ומורכבת המציאות החזותית שלנו, וכמה מאתגר לייצג אותה בצורה משכנעת במחשב.
יצירת הדמיה ממוחשבת של העולם
בתחילת הקריירה שלי עבדתי ב"פיקסאר" – אולפן המוכּר כיום בזכות סרטי האנימציה שהוא יוצר. בפיקסאר ניסו להפוך את האפקטים המיוחדים בסרטים למשכנעים יותר, באמצעות שילוב חומר שיצר המחשב עם צילומים חיים מהעולם האמיתי. כדי שהחלקים שנוצרו במחשב ישולבו בצילומים בצורה "חלקה", על התמונות שנוצרו במחשב להיות פוטו־ריאליסטיות, כלומר כאלו שלא ניתן להבחין בינן לבין תמונות מהעולם האמיתי (איור 1). לשם כך, יש ליצור תמונות תלת־ממדיות מתיאורים של האלמנטים שאמורים להופיע בסצנה. זהו השלב הראשון בתהליך בשם רֶנדֶרִינְג – הדמיה של העולם באמצעות מחשב (תוכלו ללמוד עוד על רֶנדֶרִינְג בסרטון הזה) [1]. בסופו של דבר, הבנו שניתן להשתמש ברֶנדֶרִינְג לא רק לאפקטים מיוחדים, אלא גם ליצירת סרטים שלמים במחשב, מבלי לצלם אותם בטבע. האתגר של יצירת עולם וירטואלי מציאותי הקסים אותי, וב־40–30 השנים האחרונות אני עוסק בשיפור הרֶנדֶרִינְג.

- איור 1 - הדרך לפוינט רייס (Point Reyes).
- תמונה זו, שהופקה ב־1983 בחברת "לוּקָסְפִילְם" (שלימים הפכה ל"פִּיקְסָאר"), היא דוגמה לדימוי פוטו־ריאליסטי ברזולוציה גבוהה שנוצר באמצעות מחשב. דימוי זה הוא נקודת ציון חשובה בדרך ליצירת סרטים דיגיטליים באמצעות מחשב (מקור התמונה: http://www.calgran.net/upf/recursos/ima_dig/_2_/estampes/d3_1.html).
כיצד פועל הרנדרינג? ראשית, אמנים, מעצבים ואנימטורים מספקים לנו תיאורים תלת־ממדיים (בציורים או במלל) של העולם שאנחנו רוצים לדמות. אנחנו שומרים את התיאורים האלו בתוך קובצי מחשב. כשיש לנו תיאור מלא של סצנה מסוימת, עלינו ליצור מודל ממוחשב של הסצנה כדי להמיר את התיאורים לתמונות ממשיות, כמו קובצי JPEG שאתם אולי מכירים. הדרך הפשוטה ביותר ליצור מודל ממוחשב של צורות מורכבות היא באמצעות מצולעים, כגון משולשים ומרובעים (איור 2). אנחנו מפרקים את כל הצורות המורכבות בסצנה למשולשים קטנטנים. כל דימוי מכיל בדרך כלל מיליארדי משולשים. לאחר מכן, אנחנו מתמודדים עם אחד האתגרים הקשים ביותר ביצירת רנדרינג מציאותי – לדמות את האור בצורה נכונה. הדרך הפשוטה ביותר למדל (לבנות מודל) אור בעולם המדומה במחשב היא להניח שקרני האור נעות בקווים ישרים. כדי למדל את האור בצורה נכונה, אנחנו משתמשים בטכניקה בשם ניתוב קרניים. בטכניקה זו, אנחנו עוקבים אחר הנתיבים של הקרניים המדומות בסצנה הווירטואלית שלנו, כדי להבין כיצד התאורה בדימוי אמורה להיראות.
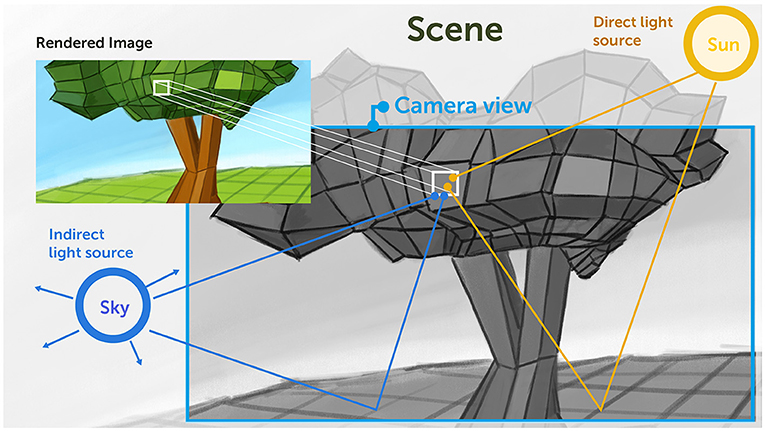
- איור 2 - הדמיית אור לשם יצירת דימויים מציאותיים.
- סצנה מורכבת מיוצגת במחשב באמצעות מקבץ העשוי להגיע למיליונים או למיליארדים של מצולעים קטנים. כדי לקבוע את הבהירות ואת הצבע של כל פיקסל בתמונה שמדמים, אנחנו מתווים את הנתיבים של קרני האור המגיעות ממקור האור, ומדמים כיצד הן מוחזרות מפני השטח שהן פוגעות בו. אנו מתחשבים בתאורה ישירה שבה האור מוחזר ישירות לעין או למצלמה. האתגר הוא תאורה עקיפה, שבה אור מהשמש פוגע בעצמים אחרים שמפזרים אור, ורק אז מגיע לעין. דוגמאות לכך הן תאורה מלמעלה שבה אור שמש מוחזר מהעננים ומהאטמוספרה, או תאורה עקיפה מגופי תאורה המותקנים על קירות מבנה. Scene = סצנה; Rendered Image = התמונה שמדמים; Indirect light source = מקור אור עקיף; Sky = שמיים; Camera view = זווית המצלמה; Direct light source = מקור אור ישיר; Sun = שמש.
מקור אור ישיר בכל סצנה, כמו השמש או נורה, פולט קרני אור. קרניים אלו נעות בחלל עד שהן פוגעות בפני השטח של עצם כלשהו ומתפזרות. כל חומר מפזר את האור בצורה הייחודית לו, כתלות בתכונות המסוימות של פני השטח שלו (לדוגמה, עד כמה הם חלקים או שקופים). עיקר העבודה שלנו כחוקרי גרפיקה ממוחשבת מתמקד בהדמיית האופן שבו חומרים שונים (למשל אבן, בד או עור) מפזרים אור. בסופו של דבר, אנחנו רוצים למצוא פונקציה מתמטית המתארת איך חומר מסוים מפזר את האור. פונקציה מתמטית זו נקראת פונקציית פיזור האור של החומר.
אחת הדרכים למדל את פונקציית הפיזור של חומר מסוים היא לייצג את פני השטח של החומר באמצעות הרבה מראות קטנות הפונות לכיוונים שונים (איור 3B). כאשר קרני האור פוגעות במראה מושלמת, הן מוחזרות ממנה בזווית השווה לזווית שבה הן פגעו בה (איור 3A). מציאת פונקציית פיזור עבור חומר באמצעות פריסה אקראית של מראות על פני השטח שלו עשויה לעבוד בצורה טובה עבור חומרים מסוימים, אך חומרים טבעיים רבים מצריכים מודלים מורכבים יותר. אפשר לקבוע את פונקציית הפיזור של חומרים מורכבים באמצעות מדידות ישירות של פיזור האור מהם. לשם כך, אנחנו מאירים על החומר ומודדים את האור המתפזר ממנו בכיוונים השונים. אנחנו יכולים לשמור את נתוני הפיזור בטבלאות או במערכים, ולהשתמש במידע הזה כדי למדל את החומר. אפשר גם להחיל על המדידות מודלים פיזיקליים.
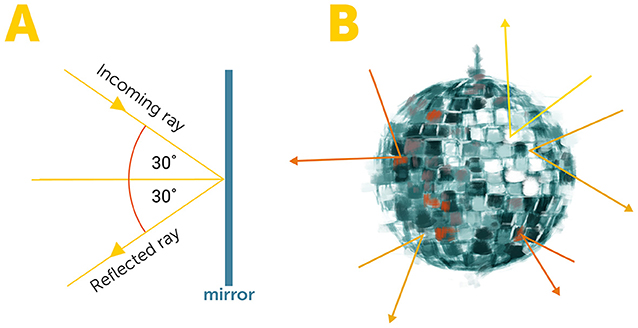
- איור 3 - מידול חומרים באמצעות מראות.
- (A) במקרה של מראה מושלמת, קרני האור מוחזרות כך שהזווית שבה הן פוגעות במראה שווה לזווית שבה הן מוחזרות ממנה. (B) אחת הדרכים הפשוטות לקבוע בקירוב את פונקציית פיזור האור של חומר מסוים היא למדל את פני השטח שלו באמצעות אוסף של מראות מושלמות, שכל אחת מהן מפזרת אור בצורה הידועה לנו. שיטה זו יעילה עבור חומרים מסוימים, בעוד חומרים אחרים דורשים מידול מורכב יותר. Incoming ray = קרן פוגעת; Reflected ray = קרן מוחזרת; Mirror = מראה.
איך העור שלך נראה טוב כל כך?
אחת הבעיות המעניינות ביותר שעבדתי עליהן הייתה איך למדל עור כך שייראה מציאותי. בסרטים הראשונים שבהם השתמשו ברנדרינג, העור נראה מלאכותי ולא בריא. זה לא מפתיע, היות שמידלו אותו כמו פלסטיק! לעור בריא יש זוהר מיוחד שגורם לו להיראות חי. בזמנו, לא היו ספרי פיזיקה שמסבירים מדוע העור נראה כך, אבל למרבה המזל, מצאתי שני מקורות מידע שעזרו לי לפצח את החידה הזו; הראשון היה מודל האטמוספרות של כוכבי לכת (כמו נוגה, מאדים או צדק), המסביר מדוע כוכבי לכת נראים כפי שהם נראים. כוכבי הלכת מוקפים לעתים בזוהר מיוחד, כמו העור – ראו למשל את התמונה הזו של צדק. מודלים אלה של האטמוספרות של כוכב הלכת מורכבים מליבה מוצקה (כוכב הלכת) המוקפת בשכבה דקה של גזים.
את הרמז השני מצאתי בספר על תולדות האמנות בספרייה של אוניברסיטת פרינסטון שבארצות הברית, המתאר כיצד הצייר ההולנדי הדגול רמברנדט צייר בציוריו עור שנראה מציאותי מאוד. הוא היה מניח שכבות של פיגמנטים ושמנים זה על גבי זה כדי ליצור את הזוהר החיוני של העור (למידע נוסף על הדרך שבה צייר רמברנדט עור, ראו כאן). רמברנדט לא הכיר את מבנה העור, אבל באופן אינטואיטיבי כלשהו הוא הבין את העובדה שהעור בנוי מכמה שכבות. בתמונות המסבירות את טכניקת הציור שלו מוצגות קרני האור נכנסות לתוך שכבות העור ובסופו של דבר מוחזרות מהשכבה העליונה שלו. באמצעות שני הרמזים הללו, פיתחתי את המודל המתמטי הראשון של פונקציית הפיזור של העור [2]. מודל זה התבסס על תהליך הנקרא החזרה מתת־פני השטח, שבו האור חודר דרך פני העור, פוגע בשכבותיו הפנימיות מתחת לפני השטח, מתפזר ואז חוזר החוצה (איור 4). רציתי שהמודל הראשון שלי יהיה פשוט ככל האפשר, אז הנחתי שהאור הנכנס ומתפזר מתחת לפני העור יוצא מאותה נקודה שבה הוא נכנס. המודל הזה דימה עור בצורה טובה למדי, וכך ידעתי שאני בדרך הנכונה.
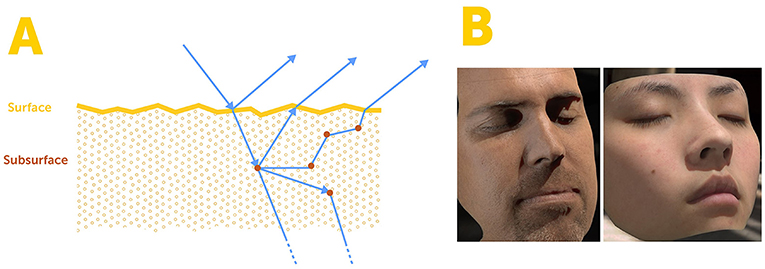
- איור 4 - החזרה מתת־פני השטח.
- (A) העור בנוי מכמה שכבות. כאשר האור פוגע בעור, חלקו מוחזר מפני השטח של העור וחלקו חודר לשכבות התת־עוריות. שם, האור מתפזר לכיוונים שונים וחלקו חוזר החוצה ממקומות השונים מאלו שהוא נכנס מהם. שילבנו את התכונה הזאת במודל המתמטי אותו פיתחנו הנתן הדמיה מציאותית של עור במחשב. (B) הדמיה של רנדרינג של עור נלקח מ-d’Eon [3]. Surface = פני השטח; Subsurface = תת־פני השטח.
עם זאת, המודל הפשוט שלי גרם לעור להיראות גבשושי, כך שבסופו של דבר פיתחתי מודל עור מורכב יותר, שבו האור יוצא מהעור בנקודה השונה מזו שהוא נכנס ממנה. אמנם המתמטיקה מאחורי הדגם נעשתה מורכבת יותר, אבל המחיר היה שווה – העור סוף־סוף נראה חלק! הסיבה שבגללה העור נראה תחילה גבשושי הייתה שאם לאזור קטן יש צד אחד מואר וצד אחר מוצל, הוא ייראה כמו בליטה. אבל אם האור שנכנס מהצד המואר מתפזר בתוך העור ויוצא בצד המוצל, גם הצד המוצל מואר. במילים אחרות, ההחזרה מתת־פני השטח של העור מפזרת את האור באופן שגורם לעור להיראות חלק.
כשניסיתי למדל שיער עברתי עוד מסע מעניין, כי גם השיער נראה בשלבים הראשונים לא מציאותי ברנדרינג. התברר שמידול שיער כגלילים צבעוניים ושקופים הוא שיטה מצוינת [4]. לאדם יש כ־100,000 שערות על הראש, וכיום בסרטים כל שערה מדומה בנפרד באמצעות מודל הגליל. מובן שיש סוגים שונים של שיער, אז מודל השיער באדם שונה מזה של פרוות בעלי חיים, למשל. עם הזמן למדו מעצבי הגרפיקה הממוחשבת כיצד למדל כל אחד מסוגי השיער. כיום, שיער מדומה נראה טוב מאוד.
כוחה של המתמטיקה בגרפיקה ממוחשבת
סימולציה של אור מצריכה שימוש במתמטיקה, כיוון שעלינו למצוא את פונקציות הפיזור הנכונות כדי לעקוב אחר תנועת קרני האור בסצנות המדומות. ואולם, למתמטיקה תפקיד מרכזי נוסף בהדמיות גרפיקה ממוחשבת; בעולם האמיתי, מספר כמעט אין־סופי של קרני שמש נכנסות לכל סצנה. כל קרן אור פוגעת בעצמים ומתפזרת אין־סוף פעמים עד שהאור מגיע לעיני הצופה. כדי לדמות בצורה מציאותית את האור בסצנה מדומה, עלינו לסכום את כל הדרכים שבהן אור יכול לנוע עד שהוא מגיע לנקודה מסוימת, במטרה לדעת כמה אור יש באותה נקודה. אין לנו אפשרות לערוך סיכום כזה בצורה אנליטית, ולכן עלינו להחליט על מספר סופי של דגימות שייצגו במדויק את כל האפשרויות. איך נוכל לדעת כמה דגימות יספיקו כדי לקבל את ההערכה הטובה ביותר של התאורה? לשם כך, אנחנו נעזרים בסימולציית מונטה קרלו [5], שהיא שיטה מתמטית ששימשה במקור לחיזוי התנהגות של חלקיקים הנעים באקראי במרחב.
כיום, לכל פיקסל בתמונת סרט מדומה נכנסות כ־1,000 קרני אור הנעות באקראי. כיוון שיש מיליארדי פיקסלים בכל תמונה, עלינו לעקוב אחר מספר עצום של קרניים בכל פריים, בכל סצנה. מצב זה מצריך חישובים רבים ויקרים. המחשבים המהירים ביותר בעולם משמשים לביצוע חישובים עבור משחקי מחשב וסרטים שיצר מחשב. בסרט טיפוסי, נדרשות שעות חישוב במחשבים המהירים ביותר, כדי לחשב תמונה יחידה. מכאן שעבור סרטים מסוימים נדרשות אפילו מיליון שעות חישוב! אמנם מדובר בזמן רב, אבל לולא הכלים המתמטיים שפיתחנו, שצמצמו דרמטית את מספר החישובים, היה זמן החישוב ארוך בכמה סדרי גודל.
בפעם הבאה שאתם צופים בסצנה שיצר מחשב בסרט, אני מקווה שתעריכו את כמות משאבי המחקר והמחשוב שהושקעו בהכנתה! כשאנחנו מסתכלים על העולם היום־יומי שלנו מנקודת מבטו של מדען המחשב, הוא נראה קסום למדי. אני מזמין אתכם לבחון את היופי בעולם בעיניים סקרניות, ולשאול את עצמכם מדוע דברים נראים דווקא כך ולא אחרת.
מילון מונחים
גרפיקה ממוחשבת (Computer Graphics): ↑ יצירת דימויים דיגיטליים באמצעות מחשבים.
רֶנדֶרִינְג (Rendering): ↑ התהליך שבו הופכים תיאור של סצנה תלת־ממדית לדימוי ממוחשב.
מודל ממוחשב (Computer Model): ↑ ייצוג של מצבים ותהליכים מהחיים האמיתיים באמצעות מחשב.
ניתוב קרניים (Ray Tracing): ↑ שיטה המשמשת ברנדרינג כדי להבין את התאורה של הסצנה באמצעות הדמיה של התנהגות האור.
פונקציית פיזור האור (Scattering Function): ↑ תיאור מתמטי של הדרך שבה חומר ספציפי מפזר את האור הפוגע בו.
החזרה מתת־פני השטח (Subsurface Reflection): ↑ סוג של פיזור אור שבו האור נכנס לחומר בנקודה אחת, מתפזר מתחת לפני השטח שלו, ויוצא מנקודה אחרת.
סימולציית מונטה קרלו (Monte Carlo Simulation): ↑ שיטה מתמטית המשתמשת בדגימה אקראית כדי לחשב את התוצאה של אירוע לא ודאי. השיטה משמשת בגרפיקה ממוחשבת כדי לדמות תאורה בסצנות דיגיטליות.
הצהרת ניגוד אינטרסים
המחברים מצהירים כל המחקר נערך בהעדר כי קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.
תודות
ברצוני להודות לאור רפאל על עריכת הריאיון שעליו מתבסס מאמר זה, ועל השתתפותו בכתיבת המאמר. תודה לאלכס ברנשטיין על האיורים, ולסוזן דבאד על העריכה.
חומרים נוספים
הצהרת כלי בינה מלאכותית
טקסט חלופי הנלווה לאיורים במאמר זה נוצר על ידי פרונטירז בסיוע כלי בינה מלאכותית, ונעשו מאמצים על מנת להבטיח את דיוקו, כולל בדיקה על ידי כותבי המאמר כאשר הדבר התאפשר. אם ברצונכם לדווח על בעיה, אנו צרו איתנו קשר.
מקורות
[1] ↑ Pharr, M., Jakob, W., and Humphreys, G. 2016. Physically Based Rendering: From Theory to Implementation. Cambridge, MA: Morgan Kaufmann.
[2] ↑ Hanrahan, P., and Krueger, W. 1993. “Reflection from layered surfaces due to subsurface scattering," in Proceedings of the 20th Annual Conference on Computer Graphics and Interactive Techniques (New York, NY). p. 165–74.
[3] ↑ d'Eon, E., Luebke, D., and Enderton, E. 2007. “Efficient rendering of human skin," in Proceedings of the 18th Eurographics Conference on Rendering Techniques (Goslar). p. 147–57. doi: 10.5555/2383847.2383869
[4] ↑ Marschner, S. R., Jensen, H. W., Cammarano, M., Worley, S., and Hanrahan, P. 2003. Light scattering from human hair fibers. ACM Transact. Graph. 22, 780–91.
[5] ↑ Harrison, R. L. 2010. “Introduction to monte carlo simulation," in AIP Conference Proceedings, Vol. 1204 (Bratislava: American Institute of Physics). 17–21.
