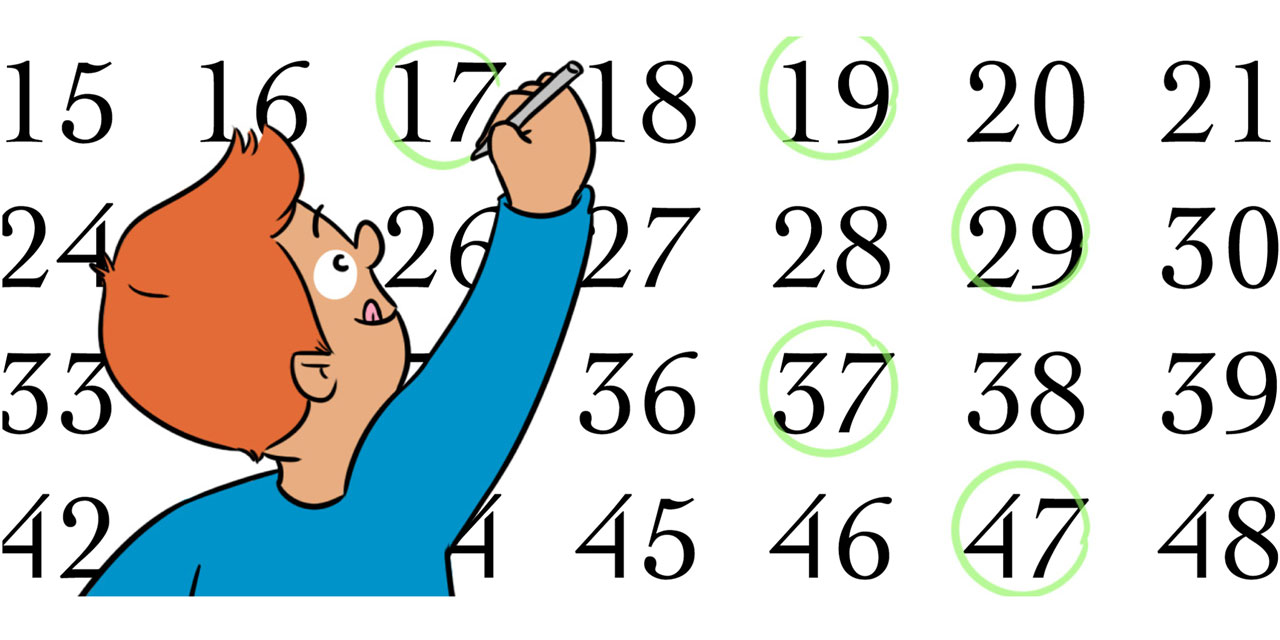תַקצִיר
משחר ההיסטוריה סיקרנו המספרים הראשוניים את האדם. מהם? מדוע השאלות הקשורות בהם כל כך קשות? אחת התופעות המרתקות ביחס למספרים ראשוניים היא התפלגותם בין כל המספרים הטבעיים. בקנה מידה קטן מופע המספרים הראשוניים נראה אקראי, אך בקנה מידה גדול נכרת חוקיות, שעד היום אינה מובנת לכל עומקה. במאמר קצר זה ננסה לעקוב אחר ההיסטוריה של חקר המספרים הראשוניים מימי קדם ועד ימינו, ובהזדמנות זאת נציץ גם אל עולמו של המתמטיקאי וננסה להבין אותו.
מספרים פריקים ומספרים ראשוניים
האם חשבתם פעם מדוע היממה מחולקת דווקא ל-24 שעות, או מדוע המעגל מחולק ל-360 מעלות? למספר 24 תכונה מעניינת: ניתן לחלק אותו במספר רב יחסית של דרכים לחלקים שלמים שווים. למשל 12 = 2 : 24, 8 = 3 : 24, 6 = 4 : 24 וכן הלאה (השלימו בעצמכם את כל הדרכים האפשריות!) כך למשל, ניתן לחלק את היממה לשני חלקים שווים בני 12 שעות כל אחד, היום והלילה. במפעל העובד ללא הפסקה במשמרות בנות 8 שעות, כל יממה מתחלקת ל-3 משמרות בדיוק.
זאת גם הסיבה בגללה חלקו את המעגל ל-360 מעלות. אם מחלקים את המעגל לשתיים, שלוש, ארבע, עשר, שתים עשרה או שלושים גזרות שוות, בכל חלוקה שכזאת, כל גזרה תהיה בת מספר מעלות שלם; ויש עוד דרכים אחרות אותן לא הזכרנו. בעידן הקדום, בו לצרכים הנדסיים או אסתטיים היה צריך לחלק את המעגל למספר גזרות שוות-גודל בדיוק גבוה, והמכשירים היחידים שעמדו לרשות השרטט היו מחוגה ומד־זווית, עובדה זאת היתה בעלת ערך שימושי רב.1
מספר שלם שניתן לכתיבה כמכפלת שני מספרים קטנים ממנו נקרא מספר פריק. למשל, הפירוקים 4 X 6 = 24 או 3 X 11 = 33 מעידים על 24 ו-33 שהם מספרים פריקים. מספר שאי אפשר לפרקו בדרך כזאת נקרא אי-פריק או ראשוני. המספרים
2, 3, 5, 7, 11, 13, 17, 19, 23, 29
כולם ראשוניים. למעשה אלו הם עשרת המספרים הראשוניים הראשונים (בדקו!).
מהתבוננות ברשימה קצרה זאת כבר עולות כמה אבחנות מעניינות. ראשית, פרט ל-2 כל המספרים הראשוניים יהיו אי-זוגיים, כי מספר זוגי הוא בהגדרתו מספר המתחלק ב-2 ולכן פריק. מכאן שהמרחק בין מספר ראשוני אחד למספר הראשוני העוקב לו הוא לפחות 2. ברשימה שלנו יש מספרים ראשוניים עוקבים שההפרש ביניהם הוא בדיוק 2 (למשל הזוג 5 ,3 או הזוג 19 ,17) ויש גם מרווחים גדולים יחסית, כמו המרווח באורך 6 בין 23 ל-29. כל אחד מבין המספרים 28 ,27 ,26 ,25 ,24 הנו מספר פריק. עוד אבחנה מעניינת היא שבעשרת הראשונה וגם בעשרת השנייה יש 4 מספרים ראשוניים, אבל בעשרת השלישית רק שניים. מה זה אומר? האם המספרים הראשוניים הולכים ונהיים נדירים יותר ויותר? מי ערב לנו שנוכל למצוא עוד ועוד מספרים ראשוניים עד בלי די?
אם בשלב זה משהו מדגדג אתכם ואתם רוצים להמשיך ולחקור את רשימת המספרים הראשוניים והשאלות שהעלינו, סימן שיש לכם נשמה של מתמטיקאי. עצרו! אל תמשיכו לקרוא!2 קחו דף נייר ועיפרון. רשמו את כל המספרים עד 100 והקיפו בעיגול את הראשוניים. בדקו כמה זוגות ראשוניים שהמרווח ביניהם הוא 2 מופיעים ברשימה. בדקו כמה ראשוניים יש בכל עשרת. האם אתם מגלים חוקיות כלשהי? או אולי הרשימה שיצרתם נראית לכם אקראית?
קצת היסטוריה, ועל מושג המשפט
המספרים הראשוניים הטרידו את החוקרים מאז ימי קדם, ואף יוחסו להם קדושה. אפילו היום, בעידן הקִדמה, יש המנסים לקשור להם תכונות מיסטיות, על-טבעיות. האסטרונום וסופר המדע הנודע קרל סייגן כתב ב-1985 ספר בשם “מגע” על חוצנים (תרבות אנושית-כביכול המתקיימת מחוץ לכדור הארץ), המנסים לתקשר עם האנושות בעזרת שדר של מספרים ראשוניים. הרעיון ששדרים של מספרים ראשוניים עשויים לשמש בסיס לתקשורת עם תרבויות חוצניות ממשיך להלהיב את דמיונם של חוקרי תרבויות כאלו גם היום.
מקובל להניח שהעניין במספרים הראשוניים החל בימי פיתגורס. תלמידיו, הפיתגוראים – ספק אנשי מדע, ספק מיסטיקנים – חיו ופעלו ביוון, במאה השישית לפני הספירה. הם לא השאירו עדויות כתובות, וכל הידוע עליהם הוא מיד שניה. שלוש מאות שנה אחריהם, במאה השלישית לפני הספירה, היתה אלכסנדריה שבמצרים הבירה התרבותית של העולם ההלניסטי. אוקלידס (איור 1), שחי באלכסנדריה בימי המלך תלמי הראשון, ידוע לרובכם מן הגיאומטריה האוקלידית הקרויה על שמו. הגאומטריה האוקלידית היא מופת לתרבות מתמטית, ונלמדת בבתי הספר בעולם המערבי כבר למעלה מאלפיים שנה. אבל אוקלידס התעניין גם במספרים. בספר התשיעי של עבודתו “יסודות”, בטענה מספר 20, מופיעה הוכחה מתמטית למשפט שקיימים אינסוף מספרים ראשוניים.

- איור 1 - האנשים שמאחורי המספרים הראשוניים.
זה המקום לומר מספר מילים על מושג המשפט וההוכחה המתמטית. משפט הנו אמירה המנוסחת בשפה מתמטית ואשר אפשר לומר עליה בוודאות אם היא מתקיימת או אינה מתקיימת במערכת נתונה. למשל המשפט “קיימים אינסוף מספרים ראשוניים” טוען שבמערכת המספרים הטבעיים (המספרים ...1,2,3) אין גבול לרשימת המספרים הראשוניים. ליתר דיוק הוא אומר שאם נכתוב רשימה סופית כל שהיא של מספרים כאלו, נוכל למצוא מספר ראשוני אחר שאינו בה. כדי להוכיח אותו לא די להצביע על מספר ראשוני נוסף לרשימה נתונה. למשל, אם נצביע על 31 כעל מספר ראשוני מחוץ לרשימת עשרת המספרים הראשוניים הראשונים שנתנו קודם לכן, אכן הראינו שאותה רשימה אינה ממצה את כל המספרים הראשוניים, אבל אולי עכשיו מצאנו את כולם ואין עוד? מה שעלינו לעשות, ומה שאוקלידס עשה לפני 2300 שנה, הוא לתת נימוק משכנע מדוע לכל רשימה סופית, ארוכה ככל שתהיה, ניתן למצוא מספר ראשוני שאינו נמצא בה. בסעיף הבא נביא את ההוכחה שלו, מבלי להכביד על הקורא יתר על המידה בסימונים.
ההוכחה של אוקלידס לקיום אינסוף מספרים ראשוניים
להוכחת הטענה על אינסופיות המספרים הראשוניים, אוקלידס השתמש במשפט בסיסי אחר שהיה ידוע לו, והוא ש“כל מספר טבעי ניתן לפרוק כמכפלה של מספרים ראשוניים”. קל להשתכנע בנכונות המשפט הזה. אם המספר שבחרתם אינו ניתן לפירוק, הוא ראשוני בעצמו. אחרת, כתבו אותו כמכפלת שני מספרים קטנים ממנו. אם כל אחד מהם ראשוני, קבלנו את מבוקשנו. אם לא, נכתוב מי מהם שהוא פריק כמכפלת מספרים קטנים ממנו וחוזר חלילה. בתהליך הזה כל פעם מחליפים את אחד הגורמים במכפלת גורמים קטנים ממנו. מאחר ואי אפשר לרדת עד בלי די, התהליך צריך להסתיים מתישהו וכל הגורמים שקיבלנו אי-פריקים, כלומר, ראשוניים. בתור דוגמא נפרק את המספר 72:
72 = 12 × 6 = 3 × 4 × 6 = 3 × 2 × 2 × 6 = 3 × 2 × 2 × 2 × 3
על סמך עובדה בסיסית זאת, נוכל להסביר עכשיו את ההוכחה היפהפייה של אוקלידס לאינסופיותם של המספרים הראשוניים. נדגים את הרעיון תוך שימוש ברשימה של עשרת המספרים הראשוניים הראשונים, אבל נשים לב שהטיעון שנביא אינו משתמש בשום תכונה מיוחדת לרשימה הזאת, ויהיה תקף לכל רשימה סופית שהיא. נכפיל את כל המספרים שברשימה זה בזה ונוסיף לתוצאה 1. נסמן את המספר שקבלנו (שאין שום טעם לחשבו, כי הטיעון צריך להיות תקף לכל רשימה, ובכל מקרה הוא מאוד מאוד גדול) ב-N:
N = (2 × 3 × 5 × 7 × 11 × 13 × 17 × 19 × 23 × 29) + 1
המספר N ניתן לפירוק, כמו כל מספר טבעי אחר, למכפלה של מספרים ראשוניים. מיהם המספרים הראשוניים המופיעים בפירוק שלו? איננו יודעים, כי לא חישבנו אותו, אבל דבר אחד אנחנו יודעים בוודאות: כל אחד מהם צריך לחלק את N. אבל המספר N משאיר שארית 1 בחלוקה בכל אחד מהמספרים הראשוניים שברשימה 29 ,23 ,... ,7 ,5 ,3 ,2. אי לכך הגורמים הראשוניים של N אינם ברשימה הזאת, ובפרט יש מספרים ראשוניים נוספים שאינם בה.
הנפה של ארתוסטנס
האם מצאתם את כל הראשוניים הקטנים מ-100? באיזו שיטה השתמשתם לשם כך? האם בדקתם כל אחד מן המספרים אם הוא מתחלק במספרים קטנים ממנו? אם בדרך זאת נקטתם, אין ספק שהשקעתם זמן רב. ארתוסטנס (איור 1), מגדולי המלומדים של התקופה ההלניסטית, חי כמה עשורים אחרי אוקלידס. הוא כיהן כמנהל הספרייה של אלכסנדריה, הספרייה הראשונה בהיסטוריה, והגדולה ביותר בעולם העתיק. הוא התעניין לא רק במתמטיקה אלא גם באסטרונומיה, מוסיקה וגיאוגרפיה. הוא היה הראשון שחישב, בדיוק מרשים לתקופתו, את היקף כדור הארץ. בין השאר הציע שיטה מחוכמת למציאת כל המספרים הראשוניים עד מספר נתון. היות והשיטה מבוססת על הרעיון של ניפוי המספרים הפריקים, היא קרויה הנפה של ארתוסטנס.
נדגים את הנפה של ארתוסטנס על רשימת כל המספרים הקטנים מ-100, שאני מקווה עדיין מצויה לפניכם (איור 2). נקיף את 2 בעיגול, שהרי הוא הראשוני הראשון, ואחר כך נמחק את כל הכפולות הגדולות יותר שלו, כלומר את כל המספרים הזוגיים הפריקים. נעבור למספר הבא שאינו מחוק, 3. מאחר ולא נמחק, אינו כפולה של מספר קטן ממנו, ועל כן נקיף אותו בעיגול – הוא ראשוני. שוב נמחק את כל הכפולות שלו הגדולות ממנו. נשים לב שחלק מהכפולות, למשל 6, כבר מחוקות, ואחרות, למשל 9, תמחקנה עכשיו. המספר הבא שאינו מחוק – 5 – שוב יוקף בעיגול, ושוב נמחק את כל כפולותיו הגדולות ממנו: 20, 15, 10 כבר מחוקות, אבל את 25 ו-35 למשל עלינו למחוק עכשיו. כך נמשיך. עד מתי? בתור תרגיל מחשבתי נמקו מדוע, אחרי שעברנו את , לא צריך להמשיך בתהליך. כל המספרים הקטנים מ-100 שלא נמחקו הנם ראשוניים ואפשר להקיפם בעיגול בבטחה!
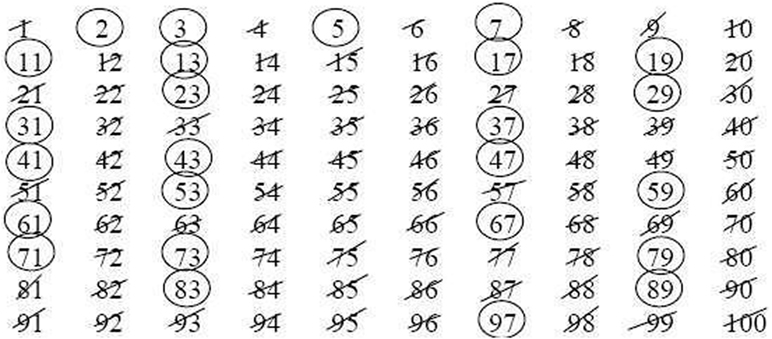
- איור 2 - הנפה של ארתוסטנס.
- המספרים הפריקים מחוקים והראשוניים מוקפים בעיגול.
שכיחות המספרים הראשוניים
מהי השכיחות היחסית של המספרים הראשוניים? כמה מספרים ראשוניים בערך יש בין 1,000,000 ו-1,001,000 (בין מיליון ומיליון ועוד אלף) וכמה בין 1,000,000,000 ובין 1,000,001,000 (בין ביליון וביליון ועוד אלף)? האם נוכל להעריך את מספר הראשוניים בין טריליון (1,000,000,000,000) וטריליון ועוד אלף?
חישובים מראים שהמספרים הראשוניים נהיים נדירים יותר ויותר. אבל האם אפשר לנסח משפט מדויק שיגיד כמה נדירים הם? משפט כזה נוסח לראשונה כהשערה על-ידי המתמטיקאי הדגול קרל פרידריך גאוס, בשנת 1793, בהיותו בן 16 בלבד. המתמטיקאי בן המאה ה-19, ברנרד רימן (איור 1), שהשפיע יותר מכל אחד אחר על חקר המספרים הראשוניים בעידן המודרני, פיתח כלים חשובים לטפל באותו משפט. אבל הוכחה ניתנה לו רק ב-1896, כמאה שנים אחרי שנוסח. באופן מפתיע ניתנו באותה שנה שתי הוכחות בלתי תלויות, על-ידי הצרפתי ז’אק אדמר ועל-ידי הבלגי דה־לה־ולה־פוסן (איור 1). מעניין לציין ששניהם נולדו בסמיכות לתאריך פטירתו של רימן. המשפט שהוכיחו זכה לכינוי “משפט המספרים הראשוניים” בגלל חשיבותו ומרכזיותו.
הניסוח המדויק של משפט המספרים הראשוניים, לא כל שכן ההוכחה שלו, דורשים כלים מתקדמים שאין באפשרותנו לדון בהם כאן. אבל ניסוח מקורב שלו אומר ששכיחות המספרים הראשוניים סביב x נמצאת ביחס הפוך למספר הספרות של x. בדוגמא לעיל, מספר המספרים הראשוניים ב“חלון” (קטע על ציר המספרים) באורך 1000 סביב מיליון יהיה ב-50% יותר גדול ממספר המספרים הראשוניים באותו “חלון” סביב ביליון (היחס הנו 6 : 9, כיחס בין מספר האפסים במיליון ובביליון) ופי שתיים בערך ממספר המספרים הראשוניים בחלון זהה סביב טריליון (כאשר יחס מספר האפסים הנו 6 : 12). ואכן, בבדיקת מחשב עולה שיש 75 מספרים ראשוניים בחלון הראשון, 49 בחלון השני ורק 37 בחלון השלישי, בין טריליון וטריליון ועוד אלף.
מי מכם שכבר נחשף למושגי הפונקציה וגרף של פונקציה, יוכל להיעזר בנוסף להסבר המעט פשטני שנתנו כאן, גם בתרשים המצורף (איור 3). בגרפים שבאיור 3 רואים כיצד משתנה (x)π, מספר המספרים הראשוניים עד x, בטווח 100 ≤ x (איור 3A), ושוב בטווח 1000 ≤ x (איור 3B). בקנה מידה קטן קשה לאתר חוקיות בגרף. אפשר להוכיח בקלות יחסית שיש מרווחים גדולים כרצוננו בהם אין אף מספר ראשוני, כלומר הגרף אינו עולה. מאידך, השערה מפורסמת (ראו להלן) אומרת שיש אינסוף זוגות של ראשוניים תאומים, שההפרש ביניהם הוא 2. אבל בקנה מידה גדול הגרף נראה חלק ומעיד על חוקיות. הניסוח המדויק של חוקיות זאת הוא משפט המספרים הראשוניים.
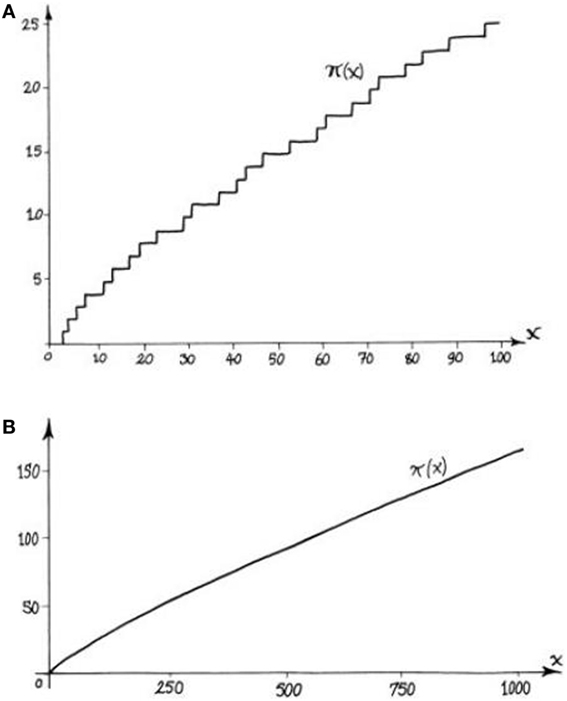
- איור 3 - שכיחות המספרים הראשוניים.
- גרפים המראים את (x)π, מספר הראשוניים עד למספר x. הגרף העליון (A) מתאר את מספר המספר הראשוניים עד x עבור x בין 0 ל-100. בגרף התחתון (B) x בין 0 ל-1000, כך שקנה המידה גדול יותר והגרף נראה יותר חלק.
העובדה שתופעה מתמטית מתנהגת בצורה אקראית בקנה מידה אחד אבל מגלה חוקיות בקנה מידה אחר, חוקיות שהולכת ונהיית מדויקת יותר ככל שקנה המידה גדל, אינה זרה למתמטיקה. מערכות הסתברותיות, כגון ניסיונות בהטלת מטבע, מתנהגות כך. אי אפשר לחזות מראש תוצאה של הטלה אחת, אבל לאורך זמן, אם המטבע אינה מזויפת, מחצית מהפעמים תיפול על ראשה. מה שמפתיע הוא שמערכת המספרים הראשוניים אינה מערכת הסתברותית, אינה תוצאה של הגרלה. זאת מערכת קבועה מראש, ואף על פי כן היא מתנהגת במידה רבה כאילו הוגרלה באקראי, בהתאם לחוקים מסוימים.
סיכום: בעיות פתוחות, או: מי רוצה להיות מיליונר
תורת המספרים, שחקר המספרים הראשוניים משתייך אליה, עשירה בבעיות פתוחות שמיטב המוחות ניסו לפצחן מאות בשנים ולא הצליחו. אחדות מהן מנוסחות כהשערות, כלומר כמשפטים שעוד לא נמצאה להם הוכחה, אך אנחנו מאמינים בנכונותם. הזכרנו כבר את ההשערה בדבר הימצאותם של אינסוף זוגות של ראשוניים תאומים – זוגות ראשוניים בהפרש 2 זה מזה. השערה מפורסמת אחרת, השערת גולדבך, אומרת שכל מספר זוגי יכול להיכתב כסכום של שני מספרים ראשוניים. למשל: 7 + 47 = 54 ,3 + 13 = 16. אם תצליחו להוכיח את ההשערה, תזכו לתהילת עולם.3
ההשערה הפתוחה המפורסמת ביותר במתמטיקה, השערת רימן, קשורה בשמו של אותו ברנרד רימן שהוזכר לעיל. במאמר מכונן על המספרים הראשוניים שפרסם בשנת 1859 ניסח השערה שחוזה באיזו מידה הקירוב למספר המספרים הראשוניים עד x, הנתון על-ידי משפט המספרים הראשוניים, חוטא לאמת. כלומר: מה ניתן לומר על “איבר השגיאה” במשפט המספרים הראשוניים – ההפרש בין המספר האמיתי והנוסחה המוצעת לו. בעיה זאת נמנית על אחת מ-7 בעיות שעל ראשן הוכרז פרס כספי של 1,000,000 דולר. אם לא הסתקרנתם דייכם, אולי פרס זה יהווה תמריץ עבורכם...
למה כל זה חשוב? את מי זה מעניין? מתמטיקאים שופטים את הבעיות שבהן הם עוסקים בראש ובראשונה בהתאם לקשיין, וליופי הפנימי שלהן. בשני מדדים אלו המספרים הראשוניים “מככבים” גבוה. אבל יש להם גם צד מעשי. חקר המספרים הראשונים מצא בעשורים האחרונים שימוש חשוב בהצפנה. הזכרנו קודם לכן את ספרו הבדיוני של קרל סייגן על תרבות חוצנית המתקשרת אתנו באמצעות המספרים הראשוניים. אבל תחום חם הרבה יותר, וכלל לא בדיוני, הוא תחום התשדורות המוצפנות, בין אם לצרכים צבאיים או אזרחיים. בבואנו למשוך כסף מכספומט. אנחנו משתמשים בכרטיס אשראי, והתקשורת בינינו לכספומט מוצפנת. כמו קודים רבים אחרים להצפנה, הקוד המצוי בכל כרטיס אשראי, הקרוי קוד RSA על שם יוצריו (ריבסט,שמיר ואדלמן) מבוסס על תכונות של המספרים הראשוניים.
סיפורם של המספרים הראשוניים עדיין אפוף מסתורין. תם ולא נשלם.
מילון מונחים
מספר פריק: ↑ מספר שלם שניתן לכתיבה כמכפלת שני מספרים קטנים ממנו, למשל: 24 = 3 X 8.
מספר ראשוני (אי־פריק): ↑ מספר שלם שאיננו מספר פריק, למשל 7 או 23.
משפט מתמטי: ↑ טענה בשפת המתמטיקה שניתן לומר עליה בוודאות אם היא נכונה או לא נכונה במערכת נתונה.
הוכחה מתמטית: ↑ סדרת היקשים לוגיים שנועדו להוכיח נכונות של משפט מתמטי. ההוכחה מסתמכת על הנחות יסוד (אקסיומות) שאומתו במערכת הנידונה, או על משפטים אחרים שכבר הוכחו קודם לכן.
השערה מתמטית: ↑ משפט מתמטי שמאמינים בנכונותו אבל עדיין לא נמצאה לו הוכחה. ה“אמונה בנכונות” יכולה לנבוע מבדיקה של מקרים פרטיים, מתימוכין חישוביים או מאינטואיציה מתמטית. יש גם השערות מתמטיות שאין לגביהן תמימות דעים והן נתונות במחלוקת.
ראשוניים תאומים: ↑ זוג מספרים ראשוניים שההפרש ביניהם הנו 2, כגון 7 ,5 או 43 ,41.
הצהרת ניגוד אינטרסים
המחברים מצהירים כי המחקר נערך בהעדר כל קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.
הערות שוליים
[1] ↑ חלוקת המעגל ל-360 מופיעה לראשונה בכתבי האסטרונומים היווניים והמצריים, אך מבוססת על חלוקה מוקדמת יותר של שעה ל-60 דקות על-ידי הבבלים. ללא ספק, זה קשור גם לעובדה כי שנת שמש נמשכת 365 ימים (בממוצע), אך, שימו לב ש- 5 X 73 = 365, ומאחר ש-5 ו-73 הם ראשוניים, 365 מתפרק להרבה פחות גורמים מאשר 360.
[2] ↑ קריאה נכונה של טקסט מתמטי הנה “קריאה פעילה” בה הקורא בודק את הנאמר, מחשב דוגמאות וכו'. אף על פי כן, אם ברצונכם לדלג על המשימה המוצעת, תוכלו לעשות זאת ואנו נחזור ונדון בה בהמשך.
[3] ↑ למרות פריצות דרך נפלאות של Zhang ו-Maynard בשנים האחרונות בהוכחת השערת המספרים הראשוניים התאומים, ההשערה עדיין פתוחה. בנוגע להשערת גולדבך, בשנת 2014 Helfgott הוכיח שכל מספר אי-זוגי גדול מ-5 הוא סכום של 3 מספרים ראשוניים.
לקריאה נוספת
[1] ↑ Du Sautoy, M. 2003. The Music of the Primes. HarperCollins.
[2] ↑ Doxiadis, A. 1992. Uncle Petros and Goldbach’s Conjecture. Bloomsbury.
[3] ↑ Pomerance, C. 2004. “Prime numbers and the search for extraterrestrial intelligence,” in Mathematical Adventures for Students and Amateurs, eds D. Hayes and T. Shubin (M.A.A), 1–4.
[4] ↑ Singh, S. 1999. The Code Book. London, Fourth Estate.