תַקצִיר
לִיאו דוּרוֹשֶר, שחקן בייסבול משנות השלושים של המאה הקודמת, אמר פעם: ”מי שנחמד מגיע למקום אחרון“. אולי זה נכון כשמדובר בבייסבול, אבל לא בחיים באופן כללי. במאמר זה נציג רעיונות מענף של מתמטיקה הנקרא ”תורת המשחקים“, ובייחוד מצב הידוע כ”דילמת האסיר“, המסביר את הקושי של אנשים רבים לשתף פעולה. תורת המשחקים מוכיחה שלאנשים מתחשבים ואמינים יש יתרון אסטרטגי, כי הם יכולים ”להחליף משחק“ ולהיחלץ מדילמת האסיר, ובחשבון הסופי כולם מרוויחים. כלומר, למעשה, ”מי שנחמד מגיע למקום ראשון“.
מבוא: לא נפסיק לשחק
”שׁוּם אָדָם אֵינֶנוּ אִי, כֻּלּוֹ מִשֶּׁל עַצְמוֹ“ (ג’ון דאן, משורר אנגלי בן המאה ה-17).
כשמדברים על ”משחקים“ מתכוונים בדרך כלל למשחקי קופסה, כמו דמקה ומונופול, או משחקי ספורט כמו כדורגל או כדורסל, או משחקי מחשב כמו פורטנייט ומיינקרפט. אבל בענף המתמטי הנקרא ”תורת המשחקים“, הכוונה היא למשחקים במובן הרבה יותר רחב.
הגדרה: מִשחק
בתורת המשחקים, מצב מסוים נחשב למִשחק כאשר:
- א. יש בו יותר מאדם אחד המבצע החלטה;
- ב. ההחלטות של כל שחקן משפיעות על השחקנים האחרים.
לפי ההגדרה הזאת, כמעט כל דבר שאנחנו עושים בחיים הוא משחק. כמעט כל פעילות - בבית, בלימודים, בכל מקום שאנחנו הולכים אליו – מתאימה להגדרה של משחק. לא משוכנעים? חישבו רגע איך התחלתם את היום. המהירות שבה קמתם מהמיטה השפיעה על הוריכם – וההחלטה שלהם לגבי שעת הקימָה השפיעה עליכם. לכן זה משחק! חישבו על כל מה שקרה בשלבים הבאים ובהמשך היום. מחדר האמבטיה לארוחת הבוקר, בכיתה ובהפסקה: אתם מקבלים כל הזמן החלטות המשפיעות גם על אחרים ולא רק עליכם. אתם משַֹחקים משחקים! היכרות עם תורת המשחקים יכולה לשפר את החוויה שלכם בכל המצבים האלה, ולאפשר לכם לא רק ”לנצח“ אלא גם לשפר את היחסים עם אחרים וליהנות יותר מהחיים.
תורת המשחקים נועדה לצפות איך יתנהגו בני אדם במצבים אסטרטגיים. יש לה שימושים בתחומי הכלכלה, מדעי המדינה, מנהל העסקים, המשפט, היזָמוּת והצבא, בין רבים אחרים. כפי שהפיזיקה, למשל, מסבירה איך כוכבי לכת סובבים סביב השמש, תורת המשחקים מנסה להסביר איך בני אדם מגיעים להחלטות במהלך מִשחקים. מתמטיקה היא כלי מועיל בתורת המשחקים, ואפשר להשתמש בה כדי לנתח את המניעים של כל שחקן ולנבֵּא את התוצאות. לפעמים, כמו בדוגמה שנביא מיד, היא מנבאת דברים די מפתיעים.
דוגמה: החברים וההמבורגרים
שמונה חברים מחליטים להיפגש לארוחה במסעדת המבורגרים. הם יחלקו את החשבון ביניהם שווה בשווה. בתפריט יש שתי אפשרויות: א. המבורגר רגיל במחיר 4 דולר, ו-ב. המבורגר דה לוקס במחיר 8 דולר. כל החברים חושבים שהמבורגר רגיל שווה מבחינתם 5 דולר, והמבורגר דה לוקס – 6 דולר. שימו לב שלהרגשתם, המבורגר רגיל שווה יותר ממחירו בתפריט (5 לעומת 4 דולר) והמבורגר דה לוקס שווה פחות (6 לעומת 8 דולר). כלומר, מבחינתם לא משתלם להזמין המבורגר דה לוקס, משום שהם ישלמו 8 דולר על מאכל ששווה לדעתם רק 6 דולר. ובכל זאת, תורת המשחקים מנבאת שכל שמונת החברים יזמינו דווקא המבורגר דה לוקס. מדוע?
כדי להבין את התוצאה המפתיעה הזאת, כדאי לחשוב על המשחק מנקודת מבט מתמטית. נאמר ש-D מייצג את מספר החברים המזמינים המבורגר דה לוקס, ו-R את מספר החברים המזמינים המבורגר רגיל .(D ו-R הם מספרים שלמים בין 0 ל-8; R + D = 8, כי מספר החברים הוא שמונה).
מאחר שהמבורגר דה לוקס עולה 8 דולר והמבורגר רגיל 4 דולר, מחיר ההזמנה יהיה 8D+4R. מכיוון ש- R = 8-D, אפשר לכתוב את הביטוי גם בצורה 8D + 4 (8-D). כשפותחים את הסוגריים מקבלים 8D + 32-4D, ואם נפשט זאת:
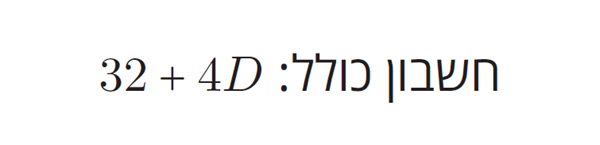
כל חבר נדרש לשלם שמינית מהחשבון. מאחר שהחשבון הכולל הוא 32+4D, כל חבר משלם 32/8+4D/8, כלומר אם נפשט:
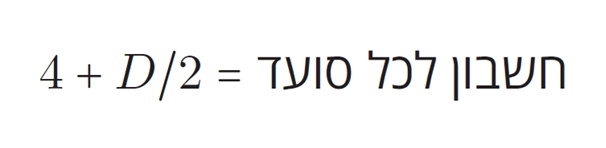
סועד שמשדרג את ההזמנה שלו מהמבורגר רגיל להמבורגר דה לוקס מקבל מנה שהערך שלה מבחינתו גבוה בדולר אחד (הרי היא שווה מבחינתו שישה דולר, ולא חמישה כמו המבורגר רגיל). אבל הוא משלם רק חצי דולר נוסף, כי הרי ארבעת הדולרים הנוספים מתחלקים בין שמונה אנשים. לכן יש לכל סועד מניע להזמין המבורגר דה לוקס – אף על פי שאם כולם יעשו זאת, כל אחד ישלם בסופו של דבר שמונה דולר על מנה ששווה מבחינתו רק שישה דולר. (ואם רק אדם אחד יזמין המבורגר רגיל? אז החשבון הכולל יירד מ-64 ל-60 דולר, והחשבון לכל סועד יהיה 7.50 דולר במקום 8. מי שהזמין המבורגר רגיל יצטרך לשלם 7.50 דולר על מנה ששווה מבחינתו רק 5 דולר – עוד יותר גרוע מאשר לשלם 8 דולר על מנה ששווה 6 דולר!)
המסקנה הזאת נשמעת אולי משונה, אבל למעשה זוהי דוגמה למצב האסטרטגי המפורסם והנחקר ביותר בתורת המשחקים – המשחק הנקרא ”דילמת האסיר“.
דילמת האסיר
אלבּרט טאקֶר, מתמטיקאי מאוניברסיטת פרינסטון ואחד מחלוצי תורת המשחקים1, פיתח את דילמת האסיר ב-1950, כדי להדגים את אחד הלקחים המפתיעים של תורת המשחקים: שבמקרים מסוימים, הבחירה במה שטוב לנו אישית היא דווקא הגרועה ביותר מבחינת כולנו.
דילמת האסיר – הסיפור
המשטרה עצרה שני אסירים – אסיר מס’ 1 (P1) ואסיר מס’ 2 (P2) – בחשד לעבירה שעונשה עד חמש שנות מאסר. אבל למשטרה יש גם חשד כבד שהשניים גם ביצעו פשע חמור יותר – שוד מזוין – שהעונש עליו הוא עד 20 שנות מאסר. חוקר המשטרה מכניס כל חשוד לחדר נפרד ואומר לו: ”הגיע הזמן שתודה בביצוע השוד המזוין. תקופת המאסר שלך תלויה בהודאה שלך ושל השותף שלך לפשע. אם רק אתה תודֶה, תצא עוד היום לחופשי. אם אף אחד מכם לא יודה, שניכם תקבלו עונש מאסר של חמש שנים; אם שניכם תודו, תקבלו עשר שנים; ואם רק השותף שלך יודה, תקבל אתה עונש מאסר של עשרים שנה.“ באיזו אפשרות יבחרו החשודים?
איור 1 מראה מה תהיה תקופת המאסר של אסיר מס’ 1 בכל אחד מהמקרים. שימו לב שבכל מקרה – גם אם אסיר מס’ 2 מודֶה וגם אם לא – משתלם לאסיר מס’ 1 להודות במעשה. (אם אסיר 2 מודה, אסיר 1 יבלה עשר ולא עשרים שנה בכלא. אם אסיר 2 אינו מודה, אסיר 1 ייצא לחופשי במקום לבלות חמש שנים בכלא. כך או כך, יש לאסיר 1 מניע אישי להודות). אותו היגיון תופס כמובן גם לגבי האסיר השני. אם כן, תורת המשחקים צופה ששני האסירים יודו במעשה, ושניהם יישבו בכלא עשר שנים – כלומר שניהם יפסידו, כי אילו היו שניהם שותקים, היו מקבלים רק חמש שנות מאסר.
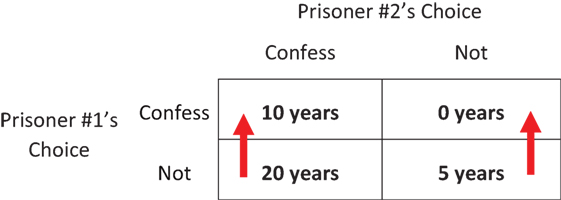
- איור 1 - זמן המאסר לאסיר מס’ 1 כתלות בהחלטה של אסיר מס’ 2.
- ”מטריצת התשלום“ שלפניכם מראה כמה זמן יבלה אסיר מס’ 1 בכלא כתוצאה מכל צירוף החלטות אפשרי שלו ושל שותפו. ארבע המשבצות מייצגות את ארבע התוצאות האפשריות של משחק זה (הברירות של אסיר מס’ 1 רשומות בשורות האופקיות, ושל אסיר מס’ 2 – בטורים האנכיים). שימו לב שבכל מקרה כדאי לאסיר מס’ 1 להודות (ראו חיצים אדומים). Prisoner #1’s Choice = החלטת אסיר מס’ 1 Prisoner #2’s Choice = החלטת אסיר מס’ 2 Confess = להודות Not = לא להודות Years = שנים.
דילמת האסיר במציאות
רוב הסיכויים שאף פעם לא תיחקרו במשטרה – אבל מצבים רבים שאנחנו נתקלים בהם בחיים מתבססים למעשה על העיקרון של דילמת האסיר, מנקודת הראות של תורת המשחקים. כדי להסביר זאת בצורה ברורה יותר, נגדיר בדיוק למה הכוונה במושג ”דילמת האסיר“. כך נוכל לזהות מתי מצב מסוים במציאות הוא ”דילמת אסיר“, גם אם אין לו שום קשר לאסירים. לשם כך צריך קודם להגדיר מושג חשוב אחר בתורת המשחקים: ”אסטרטגיה שולטת“.
הגדרה: אסטרטגיה שולטת
האסטרטגיה השולטת מבחינת כל שחקן היא הפעולה המשתלמת ביותר עבורו, בלי קשר לפעולות שבהן בוחרים האחרים.
הגדרה: דילמת האסיר
משחק מסוים הוא ”דילמת אסיר“ כאשר: א. לכל השחקנים יש אסטרטגיות שולטות, ו-ב. לכל שחקן משתלם יותר לא לבחור באסטרטגיה השולטת שלו.
ההגדרה של דילמת האסיר לא מתייחסת כלל למספר השחקנים במשחק. בסיפור הקלאסי שהבאנו כאן יש רק שני אסירים, אבל אין לכך כל חשיבות: את אותו משחק בסיסי אפשר לשחק עם כל מספר משתתפים. למשל, משחק ”החברים וההמבורגרים“ שתיארנו קודם, הוא דילמת אסיר עם שמונה שחקנים, כי יש בו אסטרטגיה שולטת (במקרה הזה, האסטרטגיה ”להתוודות“ מתחלפת באסטרטגיה ”להזמין המבורגר דה לוקס“), אבל כשכולם בוחרים בה, כולם מפסידים (”משלמים יותר מדי“ במקום ”מקבלים עונש מאסר ארוך יותר“). להלן עוד שתי דוגמאות מחיי היומיום לדילמות אסיר רבות-משתתפים:
דוגמה: השלכת אשפה
התושבים המבלים בפארק ציבורי צריכים להחליט אם לזרוק את הפסולת לפח בסוף הבילוי. מנקודת מבט אישית, קל יותר לכל אחד מהם להשאיר אותה זרוקה על הארץ – אבל אם כולם יעשו כך, הגן יהיה במצב גרוע מאוד. בדילמת האסיר הזאת, השחקנים הם האנשים המבלים בגן הציבורי, האסטרטגיה השולטת של כל שחקן היא להשאיר את האשפה על הקרקע, והיא תוביל לתוצאה גרועה עבור כולם.
דוגמה: התנגדות לבריון
בכיתה יש בריון המציק לכל הילדים. כשהוא מציק לילד מסוים, האם תבואו לעזרתו, או שתעמדו מהצד ולא תתערבו? ההעדפה האישית של כל ילד וילדה בכיתה היא לעבור בשתיקה על ההתנהגות של הבריון – אחרת הוא עלול להפנות את ההצקות אליו/אליה – אבל אם כולם ישתקו, ההצקות עלולות להימשך בלי סוף. בדילמת אסיר זו השחקנים הם תלמידים, האסטרטגיה השולטת של כל שחקן היא לא להתנגד לבריון, והתוצאה הגרועה תהיה שהוא ימשיך בהצקות.
להיחלץ מדילמת האסיר: כוחה של עזרה הדדית
”מה ששנוא עליך אל תעשה לחברך.“ (רבי הלל)
בדילמת האסיר, כל הצדדים מפסידים אם הם נוקטים בפעולה המשתלמת ביותר להם אישית, אבל מרוויחים אם הם מקריבים משהו כדי לעזור לאחרים. לכן, אחת הדרכים להיחלץ מהדילמה היא להחליף את המניע של השחקנים, כך שיהיו מעוניינים לעזור לאחרים. במקרה של השלכת אשפה, למשל, אפשר להציב בגן הציבורי שלטים ועליהם הכתובת ”שכנים טובים זורקים את האשפה לפח“. צעד כזה עשוי להניע את התושבים לנקות אחריהם, כי הם רוצים להרגיש שהם ”שכנים טובים“ – וגם לא רוצים שיחשבו עליהם כעל ”שכנים רעים“. אם הרגשות החדשים האלה יהיו חזקים מספיק כדי לשכנע את כולם לנקות, כולם ירוויחו – כי הגן הציבורי יהיה נקי, והתושבים ירגישו טוב עם עצמם ועם שכניהם כתוצאה מהתנהגותם הטובה.
להיחלץ מדילמת האסיר: כוחן של הבטחות
”גרד את גבי ואגרד את גבך.“ (ביטוי עתיק שמקורו כנראה בחיי המלחים הבריטים במאה ה-17. מקביל לביטוי ”יד רוחצת יד“ בעברית).
במאה ה-17, מלחים בריטים שנתפסו שיכורים בעת מילוי תפקידם קיבלו עונש קשה. הם נכבלו לתורן, ואחד המלָחים האחרים הצליף בהם בשוט מכאיב במיוחד שנקרא ”החתול בעל תשעת הזנבות“. כדי להציל את עצמם מפגיעות חמורות, סיכמו המלחים ביניהם שיסתפקו בהצלפות קלות (הם כּינו אותן ”גירוד“). כל עוד כולם פעלו לפי ההסכם, הם יכלו להיות בטוחים שאם ייענשו יקבלו רק הצלפה קלה.
”גרד את גבי ואגרד את גבך“ היא דוגמה של הבטחה – התחייבות לעזור, בתנאי שהאחֵר יעזור תחילה. זוהי שיטה נוספת להיחלץ מדילמת האסיר.
הבטחת האסיר
”אם אתה לא תודֶה באשמה, אני מבטיח שגם אני לא אודה. אבל אם תודֶה באשמה, גם אני אודה.“
נניח שאסיר מס’ 2 מבטיח את ההבטחה הזאת, ואסיר מס’ 1 מאמין לו. במקרה כזה, אסיר מס’ 1 צריך לבחור בין עשר שנות מאסר (אם שניהם מודים) לבין חמש שנות מאסר (אם אף אחד מהם לא מודה), ולכן הוא יבחר כמובן לא להודות בעבירה. הדילמה נפתרה! ראו איור 2. אבל מה אם אסיר מס’ 1 לא מאמין לשותפו? אם לדעתו הוא יפר את ההבטחה, אסיר מס’ 1 יודה באשמה, ושניהם יקבלו עשר שנות מאסר. הדילמה נשארה בעינה!
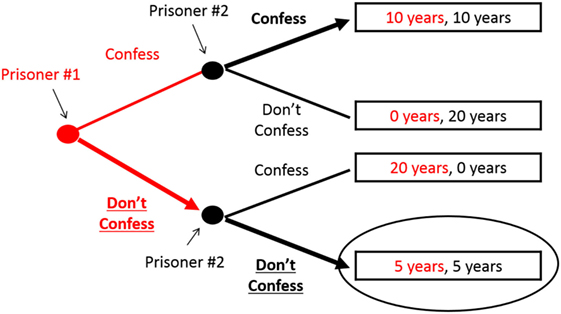
- איור 2 - ”הבטחת האסיר“ מאפשרת לשחקנים להיחלץ מ”דילמת האסיר“ זהו ”עץ המשחק“ של דילמת האסיר, כששחקן אחד (אסיר מס’ 1) עושה את המהלך הראשון, וזה שמשחק את המהלך האחרון (אסיר מס’ 2) יכול להתחייב ל”הבטחת האסיר“.
- הקווים והכיתוב האדום מתייחסים לאסיר מס’ 1, והשחורים לאסיר מס’ 2. המשחק מתחיל משמאל ומתקדם ימינה. הבחירה שכל שחקן מבצע בכל ”נקודת בחירה“ מסומנת בחץ עבה, והאפשרות שוויתר עליה מסומנת בחץ דק. התוצאה החזויה – שאף אחד מהם לא יודה בעבירה, וכל אחד יקבל חמש שנות מאסר – מסומנת בעיגול.
איך תוכלו לוודא שיאמינו להבטחות שלכם? השיטה הפשוטה והיעילה ביותר היא להקפיד לנהוג ביושר ובהגינות. אם אחרים יראו ש”מילה שלכם זו מילה“ ושאכפת לכם מהמוניטין שלכם, הם יסמכו עליכם שתקיימו הבטחות. כך תוכלו לנצל את מלוא הכוח הטמון בהבטחות, להיחלץ מדילמות אסיר שאתם נתקלים בהן, ולשפר את חייכם וגם את חיי הסובבים אתכם.
לקריאה נוספת
במאמר זה מובאות שתי שיטות להיחלץ מדילמת האסיר – החלפת מניע, והבטחה. למעשה יש חמש ”דרכי מילוט“ מהדילמה. עוד מידע על כך ועל נושאים אחרים הקשורים לתורת המשחקים תמצאו בספר שלי, Game-Changer, ובשאר הספרים המופיעים ברשימה הבאה.
ספרים המציעים מבוא קל לקריאה לתורת המשחקים:
- “Game-Changer: Game Theory and the Art of Transforming Strategic Situations” by David McAdams, 2014
- “Thinking Strategically: The Competitive Edge in Business, Politics, and Everyday Life” by Avinash K. Dixit and Barry J. Nalebuff, 1991
ספרים המתעמקים ביישומים חשובים של רעיונות בתורת המשחקים:
- “Getting to YES: Negotiating Agreement Without Giving In” by Roger Fisher and William Ury, 1981
- “Who Gets What—And Why” by Alvin E. Roth (winner of the Nobel Prize in Economics), 2015
הספר האהוב עליי בתחום תורת המשחקים:
“Games of Strategy, fourth edition” by Avinash Dixit, Susan Skeath, and David H. Reiley, Jr., 2015
הצהרת ניגוד אינטרסים
המחברים מצהירים כי המחקר נערך בהעדר כל קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.
הערת שוליים
[1] ↑ אחד מתלמידי הדוקטורט של טאקר, ג’ון נאש, זכה בפרס נובל לכלכלה על תרומתו לתורת המשחקים. הסרט זוכה האוסקר ”נפלאות התבונה“ מספר על חייו של נאש (אותו מגלם ראסל קרואו) בימי לימודיו אצל טאקר בפרינסטון.
