תַקצִיר
דמיינו שבכל פעם שאתם חוֹוִים שקיעה יפהפייה אתם מצלמים אותה ומפרסמים את התמונה באינסטגרם שלכם. התמונות הראשונות שלכם מקבלות אלפי “לייקים”, אולם יום אחד אתם מפרסמים תמונה נוספת והיא מקבלת רק “לייקים” בודדים. האם תפרסמו תמונה של השקיעה הבאה שתראו? קַבָּלַת החלטות והתבוננות בתוצאות שלהן מסייעת לנו ללמוד דברים על העולם שסביבנו, מה שמשפיע על הבחירות העתידיות שנבצע. חוקרי מוח פיתחו מודלים מתמטיים כדי להסביר כיצד אנשים לומדים מתוצאות חיוביות ושליליות של החלטות העבר שלהם. לרוב מתייחסים למודלים האלה כמודלים של למידה באמצעות חיזוק. במאמר הזה נתאר את המצבים שבהם אנו יכולים להשתמש בלמידה באמצעות חיזוק בעולם האמיתי, ונסביר כיצד משוואות מתמטיות יכולות לסייע לנו להבין את התהליך הזה, וכיצד חוקרים איך המוח לומד מחוויות כדי לקבל החלטות טובות.
מהי למידה באמצעות חיזוק?
למידה באמצעות חיזוק (Reinforcement learning) היא תהליך שבו אנו משתמשים בחוויות העבר כדי לסייע לנו לקבל החלטות שיובילו לתוצאות טובות. בואו נחזור לדוגמה שתוארה בתחילת המאמר של פרסום תמונות שקיעה באינסטגרם, ונעבור עליה ביֶתֶר פירוט. בפעם הראשונה שאתם מפרסמים תמונת שקיעה אתם מקבלים המון “לייקים”, מה שגורם לכם להרגיש שמחים – החוויה החיובית של קבלת כל ה“לייקים” האלה תגרום לכם ככל הנראה לפרסם תמונה נוספת. אתם מפרסמים תמונת שקיעה נוספת ומקבלים אותה כמות של “לייקים”. אתם מפרסמים תמונה שלישית וה“לייקים” ממשיכים לזרום. יום אחד, אתם מפרסמים תמונה שנראית לכם יפה ומקבלים מעט מאוד “לייקים”. נוסף על כך מישהו כותב הערה מרושעת על התמונה שלכם. לפתע, לא כל האסוציאציות שיש לכם ביחס לפרסום תמונות שקיעה הן חיוביות. אתם צריכים לעדכן את מה שלמדתם כדי להביא בחשבון את החוויה השלילית של קבלת הערה מרושעת. בפעם הבאה שתהיה לכם הזדמנות לפרסם תמונת שקיעה אתם עשויים להיות קצת פחות נלהבים לעשות זאת. אפשר לחשוב על התוצאות של הבחירות שלכם כאותות של חיזוק. אם אנו מקבלים החלטה וחווים משהו חיובי כתוצאה ממנה, כלומר מקבלים אות חיזוק חיובי, מרבית הסיכויים שנחזור על הבחירה הזו בעתיד. אולם אם אנו מקבלים החלטה וחווים משהו שלילי, אנו עשויים לבחור באפשרות אחרת בפעם הבאה. התהליך הזה נקרא למידה באמצעות חיזוק.
למה משתמשים במשוואות כדי להבין למידה וקבלת החלטות?
באופן כללי, חוויות חיוביות (כמו קבלת “לייקים” רבים ברשת החברתית) גורמות לציפייה שלנו לקבלת תגמול לעלוֹת, וחוויות שליליות (כמו קבלת הערות מרושעות) גורמות לציפייה לקבלת תגמול לרדת. אולם התיאור הכללי הזה של תהליך למידה אינו מסייע לנו להפיק ניבויים מסוימים על כמה חוויה מסוימת תגרום לנו לשנות את הציפיות שלנו. לדוגמה, דמיינו שאתם מפרסמים תשע תמונות שמקבלות הרבה “לייקים” ותמונה אחת שמקבלת הערה מרושעת. כמה ההערה המרושעת הזו תשנה את הערכתכם בנוגע למידת התגמול שתרגישו בעקבות פרסום תמונה? כמה פחות סביר שתפרסמו תמונה דומה בעתיד? בלי משוואה מתמטית שמתארת את תהליך הלמידה לא נוכל לענות על השאלות האלה.
נוסף על כך חוקרים יכולים לרשום משוואות עם חלקים שונים כאשר כל חלק מייצג תהליך אחר שמעורב בחשיבה או בקבלת החלטות. לאחר מכן, אנו יכולים לראות מה קורה כשאנו משנים כל חלק במשוואה כדי להבין כיצד תהליכי חשיבה שונים תורמים ללמידה.
מודל רֶסְקוֺרְלָה-וַגְנֶר
במהלך השנים, חוקרים פיתחו משוואות מתמטיות שונות, או “מודלים חישוביים” שונים, כדי להסביר כיצד אנשים לומדים מחוויות חיוביות ושליליות. אחד המודלים הראשונים, שעדיין שימושי כיום, נקרא מודל רסקורלה-וגנר (Rescorla-Wagner) [2, 1].
החוקרים רוברט רסקוֹרלה ואלן ווגנר רצו להבין טוב יותר את סדרת הניסויים המפורסמים שבוצעו על-ידי חוקר אחר, איוון פבלוֹב. בניסויים האלה פבלוב צלצל בפעמון שוב ושוב (למעשה זה היה מכשיר אחר שמייצר צליל, ושמו מֶטְרוֹנוֹם, אולם למען הפשטות נקרא לו פעמון), ואז נתן לכלבים אוכל. בהתחלה, הכלבים לא קישרו בין התגמול של האוכל ובין צליל הפעמון. אולם פבלוב מצא שאחרי כמה חזרות על התהליך הזה הכלבים התחילו לרייר כשהם שמעו את הצליל, אפילו אם לא ניתן להם אוכל. הממצאים האלה מציעים שבמשך הזמן הכלבים למדו לְקַשֵּׁר בין הפעמון ובין קַבָּלַת אוכל באופן כזה שהם ציפו לקבלת אוכל (והתחילו לרייר!) בכל פעם שהם שמעו את הפעמון.
אולם כפי שצוין קודם, למידה היא לרוב תהליך הדרגתי שמורכב מצעדים קטנים. משמעות הדבר היא שבכל פעם שהכלבים של פבלוב שמעו את הפעמון וניתן להם אוכל, עוצמת הקישור שבין הפעמון ובין האוכל התחזקה קצת, וגדל הסיכוי שהכלבים יריירו לְמִשְׁמַע צליל הפעמון.
האם אנו יכולים לנבּא כמה חזק הכלבים מצפים לקבל אוכל כשהם שומעים פעמון? האם אנו יכולים לדעת כיצד הניבויים של הכלבים ישתנו אחרי כל חוויה? רסקורלה ווגנר רצו לנסח משוואה מתמטית כדי לענות על השאלות האלה. אולם הם לא יכלו לכתוב כל משוואה, אלא הם היו צריכים לכתוב משוואה שתתאר באופן מדויק את תהליך הלמידה. כדי לעשות זאת הם היו צריכים ראשית להבין את המצבים שבהם חיות לומדות במטרה לְפַתֵּחַ קישורים (אסוציאציות) בין החוויות שלהן.
במקום לערוך ניסויים נוספים עם כלבים, פעמונים ואוכל, רסקורלה ווגנר ערכו את רוב ניסוייהם בחולדות באמצעות צליל ושוק חשמלי. בניסויים האלה חולדות היו שומעות צליל ואז מקבלות שוק חשמלי. באופן רגיל החולדות היו רצות בכלוביהן. אולם מאחר שחולדות אינן אוהבות לקבל שוק חשמלי, הן לעיתים קרובות היו קופאות כשחשבו שהשוֹק עומד להתרחש. עוצמת הקישור שהתפתח אצל החולדות בין השוק ובין הצליל ניתנת למדידה באמצעות מידת הקיפאון שחולדות מפגינות כשהן שומעות את הצליל. לדוגמה, בפעם הראשונה שחולדה שומעת את הצליל היא לא תצפה לקבל את השוק, ולכן היא תמשיך לזוז בכלוב כרגיל. אולם אם היא תשמע את הצליל ואז תקבל שוק, היא תתחיל ללמוד שהצליל והשוק קשורים זה לזה. בפעם הבאה שהיא תשמע את הצליל, החולדה תתחיל לזוז פחות ולקפוא במקום יותר.
רסקורלה ווגנר הבחינו בכך שבתחילת התהליך, כאשר החולדות התחילו ללמוד על הקשר שבין הצליל ובין השוק, הן הראו שינויים גדולים יותר בתדירות ובמשך הזמן שהן קפאו. אחרי שהן קיבלו שוקים רבים הן הגיעו לתבנית התנהגות יציבה יותר – הן המשיכו לקפוא, אולם כמות הזמן שהן קפאו גדלה מעט מאוד אחרי כל שוק.
האבחנה הזו, כמו גם ניסויים רבים אחרים, הובילה את רסקורלה ווגנר לגלות כי למידה באמצעות חיזוק מוּנַעַת על-ידי הפתעה. במילים אחרות, חיות לומדות יותר כשהן פוגשות במשהו שהן לא ציפו לו. הם קראו לסוג ההפתעה הזה במהלך למידה בשם “טעות ניבּוי”, מאחר שהיא מייצגת את המידה שבּה הניבוי של החיה על מה שהיה צפוי להתרחש היה שונה ממה שהיא חוותה. לדוגמה, בפעם הראשונה שהכלבים של פבלוב שמעו פעמון לא הייתה להם סיבה לצפות לקבל אוכל. כשהם קיבלו אוכל, הם חוו הפתעה – או טעות ניבוי גדולה – מאחר שהאירוע שהתרחש (אוכל!) היה שונה מאוד ממה שהם ציפו לו (כלום!). טעות הניבוי הזו גרמה להם ללמוד שהם עשויים לקבל אוכל כשהם שומעים פעמון. כשהם כן קיבלו אוכל בפעם הבאה שהם שמעו פעמון, טעות הניבוי שלהם קָטְנָה מאחר שהם היו קצת פחות מופתעים מהתוצאה. ככל שהם המשיכו לשמוע פעמון ולקבל אוכל הציפיה שלהם על כך שהפעמון מנבא קבלת אוכל המשיכה להתחזק, אולם כבר לא במידה גדולה כמו בפעמים הראשונות שבהן הם היו יותר מופתעים מקבלת האוכל.
אנו חווים “טעויות ניבוי” כל הזמן. לדוגמה, אתם עשויים לחשוב שאינכם אוהבים לאכול ברוקולי. אולם יום אחד אתם עשויים להחליט לנסות ברוקולי ולגלות שלמעשה הוא די טעים! במקרה כזה, החוויה שלכם של אכילת ברוקולי תהיה שונה מהניבוי שלכם שברוקולי הוא מגעיל. אתם תחוו טעות ניבוי, וזה יגרום לכם ללמוד משהו על ברוקולי ולשנות את אמונתכם בנוגע לכמה הוא טעים.
ללא טעויות ניבוי איננו לומדים שום דבר דרך חיזוק. למשל, ייתכן שאתם אוהבים לאכול פיצה. יום אחד אתם עשויים לעצור ולקנות פיצה בדרך הביתה מבית הספר. היא טעימה מאוד! במקרה כזה חוויית אכילת הפיצה אינה שונה מהניבוי שלכם. אתם לא תחוו טעות ניבוי, ולכן אתם לא תלמדו שום דבר חדש. אתם תמשיכו לחשוב שפיצה טעימה מאוד.
רסקורלה ווגנר רשמו משוואה מתמטית כדי לתאר את תהליך הלמידה הזה. המשוואה שלהם מציינת שהַגְּדִילָה בעוצמה שבּה החיה מקשרת משהו עם תגמול (כמו פעמון עם אוכל) מחושבת באמצעות לקיחת ההפרשׁ בין כמה תגמול החיה קיבלה ובין כמה תגמול החיה ציפתה לקבל (איור 1).
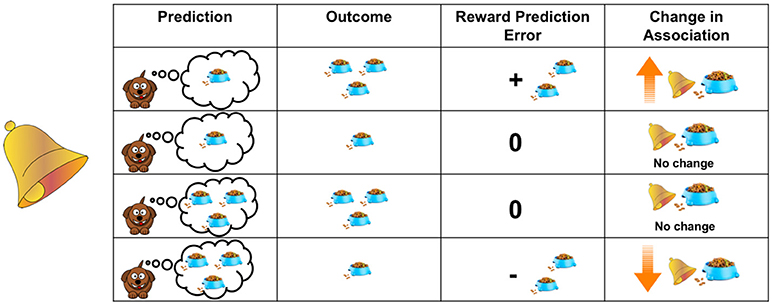
- איור 1 - למידה שמוּנַעַת מטעויות ניבוי.
- הטבלה מציגה דוגמאות שונות לאופן שבו ניבויים של הכלב וחוויות שנחווּ משפיעים על מה שהוא לומד. המידה שבה הכלב מגביר את עוצמת הקישור בין הפעמון לאוכל (עמודה ראשונה מימין) נקבעת על-ידי ההפרש שבין כמות האוכל שהכלב קיבל כשהוא שמע את הפעמון (עמודה שנייה משמאל) ובין הכמות שהוא ציפה לקבל (עמודה ראשונה משמאל). מתייחסים להפרש הזה כטעות ניבוי התגמול (עמודה שלישית).
המשוואה הזו יכולה לומר לנו כמה חזק החיה מקשרת בין שני דברים, או לכמה תגמול היא מצפה שהחלטה מסוימת תגרום, כמו בדוגמה של פרסום תמונה באינסטגרם.
נוסף על המונח החשוב של טעות הניבוי במשוואה, ישנוֹ מושג נוסף שנקרא “קצב הלמידה”. קצב הלמידה אומר לנו עד כמה החיה מעדכנת את הציפיות שלה אחרי כל חוויה, והוא מוכפל על-ידי טעות הניבוי. אנו יכולים לחשוב על קצב הלמידה בתור ייצוג של המהירוּת שבה החיה לומדת. אם לחיה יש קצב למידה גבוה היא תעדכן את הציפיות שלה הרבה כשהיא תחווה טעות ניבוי. אולם אם לחיה יש קצב למידה נמוך היא עשויה להתבסס יותר על כל חוויות העבר שלה, ולשנות רק במעט את הציפייה שלה בכל פעם שהיא חווה טעות ניבוי.
כיצד המוח לומד מחיזוק?
מודלים של למידה באמצעות חיזוק היו מוצלחים בלסייע לנו להבין כיצד מוחות לומדים. המוח מורכב מסביבות 100 מיליארד תאים שנקראים תאי עָצָב (נוירונים). תאי עצב משחררים כימיקלים שנקראים מוליכים עצבּיים (נוירוטרנסמיטרים) אשר מסייעים לתאי העָצָב לשלוח (להעביר) ביניהם הודעות. דּוֹפָּמִין הוא אחד המוליכים העצביים החשובים ביותר במוח. תאי עצב שרגישים לדופמין מגיבים לתגמולים שאנו חווים בסביבתנו.
באמצעות שימוש בניסויים כמו אלה שתוארו קודם לכן, מדענים הראו כי הפעילוּת של תאי עצב שרגישים לדופמין ממלאה תפקיד חשוב בייצוג של טעויות ניבוי במוח. אחרי שמתרחשת למידה, תאי העצב האלה מראים עלייה בפעילות בתגובה למשהו שמנבא תגמול, כמו למשל פעמון, לפני שהחיה אפילו קיבלה את התגמול. אם החיה מצפה לקבל תגמול ואז אינה מקבלת אותו, תאי העצב האלה יפחיתו את פעילותם. במונחים של מודל הלמידה באמצעות חיזוק, אנו יכולים לחשוב על דופמין בתור אות ניבוי טעות – הפעילות של תאי עצב שרגישים לדופמין מצביעה על הבדלים בין כמות התגמול שחשבנו שנקבל ובין כמה תגמול קיבלנו בפועל [3]. זה מסייע לנו ללמוד מהחיזוק, ובסופו של דבר מסייע לנו להשתמש בחוויות העבר שלנו כדי לקבל החלטות שאנו חושבים שיובילו אותנו לקבלת תגמולים (איור 2).
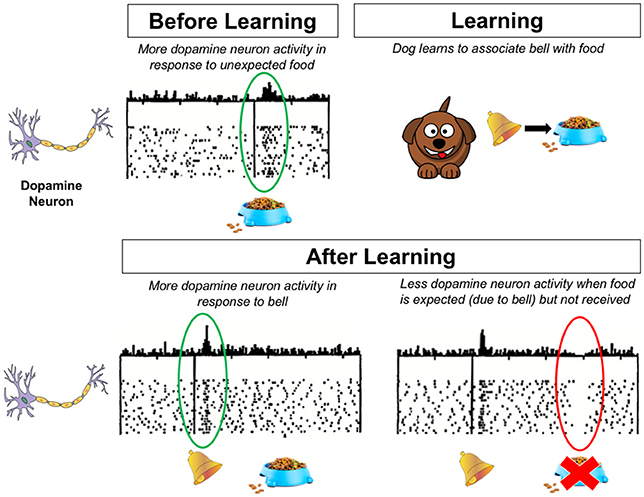
- איור 2 - מה קורה במוחו של כלב לפני למידה ואחריה.
- תאי עצב שרגישים לדופמין מגיבים לתגמולים ולניבויים על תגמולים. הנקודות מייצגות פעילות של תאי העצב האלה במשך הזמן. גובה הקווים מעל לנקודות מייצג את מספר הנקודות שנמצאות מתחתם, עבור נקודת זמן מסוימת. תאי עצב שרגישים לדופמין מגיבים לתגמול, כמו אוכל (משמאל למעלה). אחרי שהכלב לומד לְקַשֵּׁר בין הפעמון ובין האוכל, תאי העצב שרגישים לדופמין יכולים להגיב למשהו שמנבא תגמול, כמו פעמון (משמאל למטה). שימו לב לכך שתאי העצב שרגישים לדופמין לא יגיבו לאוכל עצמו במקרה הזה מאחר שהוא כבר לא מפתיע. אולם אם התגמול שנובא לא מתרחש, התאים האלה יהפכו להיות פחות פעילים (מימין למטה). התמונה נלקחה מ- Schultz ואחרים [3]. Dopamine Neuron = תא עצב שרגיש לדופמין.
אזורים שונים רבים במוח מראים תבניות פעילוּת אשר נראות דומות לאותות ניבוי הטעות שמפיקים תאי עצב שרגישים לדופמין. אזור אחד כזה במוח הוא רשת של תאים הממוקמת עמוק בחלק הפנימי של המוח, וידועה בשם גַּנְגָּלְיַית הבסיס. גנגליית הבסיס חשובה לא רק כדי לסייע לנו ללמוד אלא גם עבור שליטה בתנועות ובהֶרְגֵּלִים שלנו. החלק הגדול ביותר בגנגליית הבסיס הוא הסְטְרִיאָטוּם. הסטריאטום הוא האתר העיקרי של שחרור דופמין, והוא חלק מרכזי במערכת המוחית ששולטת על תגובותינו לתגמולים.
מחקרים רבים שבוצעו בחיות ובבני אדם הראו שפעילות בסטריאטום מקושרת לטעויות ניבוי, וממלאה תפקיד מרכזי בלמידה באמצעות חיזוק [4]. דפוסים של פעילות מוחית שקשורים בטעויות ניבוי יכולים גם להיראות בקליפת המוח הקדמית, אזור שמעורב בקבלת החלטות. הסטריאטום וקליפת המוח הקדמית מחוברים זה לזה באמצעות קשרים רבים, ונחשבים מכריעים בביצוע מהיר של החישובים אשר מתוארים במשוואות הלמידה באמצעות חיזוק. הַקְּשָׁרִים האלה עשויים להסביר כיצד אנו יכולים ללמוד במהרה מהחוויות שלנו, ולהשתמש ביֶדַע הזה כדי לסייע לנו בקבלת החלטות בעתיד (איור 3).
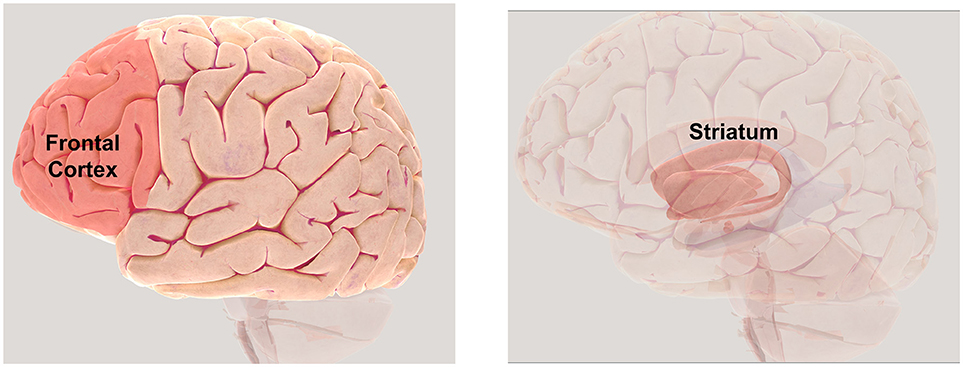
- איור 3 - אזורים מוחיים שמעורבים בלמידה באמצעות חיזוק.
- קליפת המוח הקדמית (משמאל) ממוקמת בחלקו הקדמי של המוח (מאחורי המצח) וממלאה תפקיד חשוב בקבלת החלטות, והסטריאטום (מימין) מראֶה פעילות שקשורה לטעויות ניבוי. זכויות היוצרים שייכוֹת ל- Copyright Society for Neuroscience (2017). כדי לחקור יותר את המוח באמצעות מפה תלת-ממדית, בקרו באתר http://www.brainfacts.org/3d-brain.
בכל זאת, השינויים שנצפו בפעילות בסטריאטום ובקליפת המוח הקדמית הם רק פיסה קטנה מהפאזל! חשוב לזכור שהמוח מורכב מהרבה חלקים קטנים שונים שעובדים יחד כדי לסייע לנו לחשוב ולבצע את הדברים המורכבים שאנו לומדים. מדענים ממשיכים לחקור כיצד הסטריאטום, קליפת המוח הקדמית ואזורים מוחיים אחרים פועלים יחד כדי לסייע לנו ללמוד מחיזוק, ובסופו של דבר לקבל את ההחלטות הטובות ביותר שאנו יכולים לקבל בהתבסס על המידע שלמדנו. במאמר הזה אומנם סקרנו את מודל הלמידה הקלאסי – מודל רסקורלה-וגנר – אולם ישנם מודלים מתמטיים רבּים נוספים אשר מנסים לסייע לנו להבין למידה וכיצד היא מתרחשת במוח.
לכן, בפעם הבאה שאתם חושבים אם לפרסם תמונה באינסטגרם, זיכרו שבאותו הזמן המוח שלכם פותר מהר בעיות מתמטיות, בלי שאתם אפילו מוּדעים לכך!
מילון מונחים
מודל חישובי (Computational model): ↑ מודל חישובי הוא ייצוג מתמטי פשוט של תהליך מורכב יותר. מודל הלמידה מבוססת החיזוק שמתואר במאמר הזה הוא משוואה שיכולה לייצג את תהליכי החשיבה שמעורבים בסוגים מסוימים של למידה.
טעות ניבוי (Prediction error): ↑ טעויות ניבוי מייצגות הפתעה. הן מייצגות את ההבדלים בין מה שהחיה ציפתה לחוֹות ובין מה שהיא חוותה בפועל.
קצב הלמידה (Learning rate): ↑ קצב הלמידה של חיה מייצג כמה מהר היא מעדכנת את האמונות שלה בהתבסס על מידע חדש.
דופמין (Dopamine): ↑ דופמין הוא סוג מיוחד של כימיקל במוח שנקרא מוליך עצמי (נוירוטרנסמיטר), אשר לעיתים קרובות מעורב באיתוּת על תגמולים.
הצהרת ניגוד אינטרסים
המחברים מצהירים כי המחקר נערך בהעדר כל קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.
מקורות
[1] ↑ Rescorla, R. 1998. Pavlovian conditioning. Am Psychol. 43:151–60.
[2] ↑ Rescorla, R., and Wagner, A. R. 1972. “A theory of Pavlovian conditioning: variations in the effectiveness of reinforcement and nonreinforcement,” in Classical Conditioning II: Current Research and Theory, eds A. H. Black and W. F. Prokasy (New York, NY: Appleton-Century-Crofts). p. 64–99.
[3] ↑ Schultz, W., Dayan, P., and Montague, P. R. 1997. A neural substrate of prediction and reward. Science 275:1593–9.
[4] ↑ Dayan, P., and Niv, Y. 2008. Reinforcement learning: the good, the bad and the ugly. Curr Opin Neurobiol. 18:185–96. doi: 10.1016/j.conb.2008.08.003
