Résumé
La pratique des mathématiques simples semble être un exercice courant. 2 + 2 font 4 en France et en Chine. 7 × 8 est égal à 56 aux États-Unis d’Amérique et en Allemagne. Certes, nous utilisons tous les mêmes symboles pour écrire les nombres (1, 2, 3, 4, …), mais nous employons d’autres mots pour ces derniers, simplement parce que nous parlons des langues différentes. Dans le présent article, nous donnerons des exemples de nombres en lettres dans différentes langues. Nous montrerons aussi comment les nombres avec plusieurs chiffres sont construits et comment ils peuvent faciliter ou compliquer l’apprentissage des mathématiques et la gestion des grands nombres.
Les nombres et les mathématiques sont universels
La pratique des mathématiques simples1 semble être un exercice courant que tout le monde fait. Même les très jeunes enfants le font avant d’aller à l’école, par exemple lorsqu’ils comptent des billes. Cette réalité s’applique aussi aux calculs : 2 + 2 = 4 en France et en Chine. 7 × 8 = 56 aux États-Unis et en Allemagne.2 La plupart des pays utilisent le système de numérotation indo-arabe pour écrire les nombres. Ce système utilise dix symboles auxquels tu es probablement habitué : 1, 2, 3, 4, 5, 6, 7, 8, 9 et 0. Ces dix symboles servent à écrire des nombres à un seul chiffre et nous les combinons pour obtenir des nombres à plusieurs chiffres.
Les nombres à plusieurs chiffres obéissent à la règle de la valeur de position, qui nous permet d’écrire autant de nombres que nous souhaitons avec les dix symboles que nous connaissons déjà.
La règle de la valeur de position signifie que l’on ne peut déterminer la valeur d’un chiffre qu’en fonction de sa place dans un nombre à plusieurs chiffres. Par exemple, la valeur de 9 dans 92 est 90 (9 × 10) et celle de 2 dans 92 est 2 (2 × 1). Toutefois, dans 29 c’est le contraire : la valeur de 9 est seulement 9 (9 × 1) et celle de 2 est 20 (2 × 10). C’est pourquoi 92 est différent de 29, même si les deux nombres sont le résultat d’une combinaison des mêmes chiffres.
Avoir les mêmes règles et les mêmes symboles est important, car cela permet de mieux aborder les nombres et les calculs. Cela revient presque à dire qu’il existe un seul langage mathématique dans le monde et que s’instruire en mathématiques dans un pays est suffisant pour comprendre les mathématiques n’importe où ailleurs. Où que tu sois, 2 + 2 = 4.
Les langues nomment les nombres différemment, ce qui peut faciliter ou compliquer l’apprentissage des mathématiques
Un seul petit problème se pose. Certes nous utilisons presque tous les mêmes symboles pour écrire les nombres, mais nous employons des mots différents pour ces derniers parce que nous parlons des langues différentes. Le Tableau 1 présente des exemples de nombres en lettres de 1 à 10 dans différentes langues. Comme tu peux le constater, ils diffèrent considérablement d’une langue à une autre, tout comme la plupart des autres mots. La connaissance des nombres de 1 à 10 et de leurs sens dans une langue constituent l’une des premières et des plus importantes étapes dans l’apprentissage des mathématiques. Toutefois, apprendre dix nombres en lettres est aussi difficile pour les enfants qui parlent plusieurs langues. Finalement, ils doivent apprendre dix nouveaux nombres, voire onze si nous considérons 0 et 10.
| Mandarin | English | French | German | Basque | Hindi | ||
| 0 | ling | zero | zéro | null | zero, hutsa | shuniye | 0 |
| 1 | yi | one | un | eins | bat | ek | 1 |
| 2 | èr | two | deux | zwei | bi | do | 2 |
| 3 | sān | three | trois | drei | hiru | teen | 3 |
| 4 | sì | four | quatre | vier | lau | chat | 4 |
| 5 | wǔ | five | cinq | fünf | bost | panch | 5 |
| 6 | liù | six | six | sechs | sei | cheh | 6 |
| 7 | qi | seven | sept | sieben | zazpi | saat | 7 |
| 8 | bā | eight | huit | acht | zortzi | aath | 8 |
| 9 | jiǔ | nine | neuf | neun | bederatzi | nao | 9 |
| 10 | shí | ten | dix | zehn | hamar | das | 10 |
| 11 | shí yi [dix un] |
eleven [onze] |
onze | elf [onze] |
hamaika [dix un] | gyaarah [un dix] |
11 |
| 12 | shí èr [dix deux] |
twelve [douze] |
douze | zwölf [douze] |
hamabi [dix deux] |
baarah [deux dix] |
12 |
| 13 | shí sān [dix trois] |
thirteen [trois dix] |
treize | dreizehn [trois dix] |
hamahiru [dix trois] |
tehrah [treize] |
13 |
| 16 | shí liù [dix six] |
sixteen [six dix] |
seize | sechzehn [six dix] |
hamasei [dix six] |
saulah [seize] |
16 |
| 17 | shí qi [sept dix] |
seventeen [sept dix] |
dix-sept | siebzehn [sept dix] |
hamazazpi [dix sept] |
satrah [dix-sept] |
17 |
| 20 | èr shí [deux dix] |
twenty [vingt] |
vingt | zwanzig [vingt] |
hogei [vingt] |
bees [vingt] |
20 |
| 21 | èr shí yi [deux dix un] |
twenty-one [vingt un] |
vingt et un | einundzwanzig [un et vingt] |
hogeita bat [vingt et un] |
ikis [un et vingt] |
21 |
| 29 | èr shí jiǔ [deux dix neuf] |
twenty-nine [vingt neuf] |
vingt-neuf | neunundzwanzig [neuf et vingt] |
hogeita bederatzi [vingt et neuf] |
unatis [trente moins un] |
29 |
| 48 | sì shí bā [quatre dix huit] |
forty-eight [quarante huit] |
quarante-huit | achtundvierzig [huit et quarante] |
borrogeita zortzi [quarante et huit] |
adtalis [huit et quarante] |
48 |
| 75 | qi shí wǔ [sept dix cinq] |
seventy-five [septante cinq] |
soixante- quinze | fünfundsiebzig [cinq et septante] |
hirurogeita hamabost [soixante et quinze] |
chiyahatar [cinq et septante] |
75 |
| 97 | jiǔ shí qi [neuf dix sept] |
ninety-seven [nonante-sept] |
quatre-vingt -dix-sept | siebenundneunzig [sept et nonante] |
laurogeita hamazazpi [huitante et dix sept] |
sataanave [sept et nonante] |
97 |
| 100 | yì bǎi [un cent] |
one hundred [cent] |
cent | (ein)hundred [(un) cent] |
ehun [cent] |
ek sau [un cent] |
100 |
- Tableau 1 - Nombres en lettres dans différentes langues. Pas d’inquiétude, tu n’as pas besoin de les examiner tous en détail. Regarde juste ceux qui sont écrits en bleu, car ils ont quelque chose de spécial par rapport aux nombres en mandarin, qui sont très réguliers. Tu peux également voir la traduction des nombres à deux chiffres en anglais. La construction de ces nombres est assez compliquée. Si tu veux savoir comment les prononcer, regarde sur internet. Pour le mandarin, l’anglais, l’allemand et l’hindou, rends-toi sur bing.com/translator et écris le nombre en question. Pour le basque, regarde ces vidéos Youtube : https://www.youtube.com/watch?v=6eb0J4Vg5ysfeature (nombres de 1 à 19), https://www.youtube.com/watch?v=wPbYCBzsw2Afeature (nombres de 20 à 39).
L’apprentissage des nombres en lettres plus grands que dix diffère beaucoup d’une langue à une autre (fais le jeu de la Figure 1). Dans certaines langues, la manière dont les nombres à plusieurs chiffres sont désignés est très simple et très claire. Le mandarin (la langue la plus répandue en Chine) est une de ces langues. En mandarin, le nombre 29 se traduit par « deux-dix-neuf » et 97 par « neuf-dix-sept ». Une telle langue est qualifiée de « transparente » par les scientifiques. Ce qui signifie qu’en mandarin, les nombres en lettres traduisent précisément la manière dont on écrit ceux à plusieurs chiffres et démontrent clairement la règle de la valeur de position : 97 = 9 x 10 + 7 = « neuf-dix-sept ».
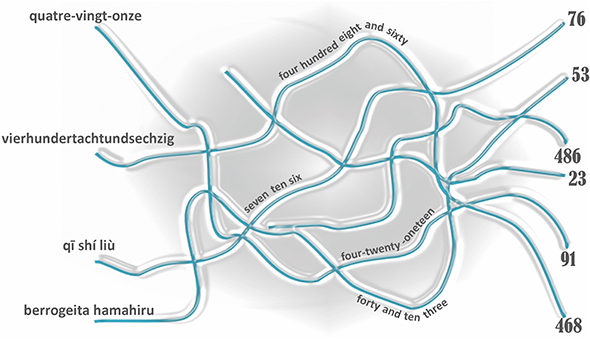
- Figure 1 - Quel nombre en lettres sur la gauche correspond à quel nombre indo-arabe sur la droite ?
- Essaye de trouver la réponse par toi-même puis suis la ligne afin de savoir si tu as raison. Cet article propose certains indices qui peuvent t’aider à trouver la bonne réponse et le Tableau 1 peut aussi t’être utile.
Les scientifiques ont constaté que l’apprentissage des mathématiques et la gestion des nombres à plusieurs chiffres sont plus faciles pour les enfants qui parlent une langue avec des nombres faciles. Toutefois, le problème est que toutes les langues n’utilisent pas nécessairement des nombres faciles. Mais alors, à quoi ressemblent les nombres complexes ? Examine les mots qui correspondent à 97. En basque (langue principalement parlée dans une région du nord de l’Espagne), on dit « laurogeita hamazazpi », qui veut dire « quatre-vingt-dix-sept » (80 + 17). En français, nous disons « quatre-vingt-dix-sept », (4 × 20 + 10 + 7). La construction de ces nombres est vraiment compliquée. En hindi (l’une des langues les plus répandues en Inde), certains nombres nécessitent même la soustraction plutôt que l’addition pour former un nombre en lettres. Par exemple, le nombre 29 se dit « unatis », qui signifie « un avant trente » (30-1).
Le Tableau 1 indique les nombres à plusieurs chiffres dans différentes langues. Tous ceux qui sont en bleu sont, d’une certaine manière, uniques. L’apprentissage des nombres de la dizaine est particulièrement difficile dans beaucoup de langues. Ne serait-il pas plus simple de dire « un-dix-deux » au lieu de « douze » pour 12 ? Douze est un nouveau nombre qu’il faut apprendre, alors que « un-dix-deux » (comme en mandarin) pourrait simplement servir de règle générale. Dans certaines langues, on change parfois l’ordre des nombres pour désigner les unités en premier. Cette permutation est ce qu’on appelle l’inversion des nombres. En anglais, seuls quelques nombres de la dizaine (de treize à dix-neuf) sont permutés. Dans d’autres langues comme l’allemand, le néerlandais, l’arabe ou le maltais, tous les nombres à deux chiffres connaissent l’inversion (97 est « siebenundneunzig » en allemand; ce qui veut dire « sept et quatre-vingt-dix »). Les grands nombres sont encore plus confus. Le nombre allemand 234 se traduit par « deux-cent-quatre-et trente ». Dans cet exemple, on prononce d’abord le chiffre de gauche, puis celui de droite et enfin celui du milieu. C’est compliqué, n’est-ce pas?
C’est d’ailleurs pourquoi les enfants qui parlent des langues avec des nombres permutés ont du mal à traiter les nombres à plusieurs chiffres. Les enfants allemands (permutation nécessaire) commettent par exemple 5 fois plus d’erreurs que les jeunes japonais (aucune permutation requise) quand ils doivent écrire des nombres [1]. Près de la moitié de leurs erreurs est due à la confusion quant à l’ordre normal des nombres [2]. Par exemple, lorsqu’ils entendent « cinq-et-quarante », ils écrivent souvent 54 au lieu de 45. Tout enfant qui grandit avec un système de nombres plus transparents peut donc se réjouir de pouvoir les apprendre plus facilement.
Toutefois, avec de la pratique, la plupart des gens comprennent comment ça marche
Nous savons déjà que les enfants qui parlent une langue avec des nombres non transparents rencontrent plus de difficultés avec les mathématiques que ceux dont la langue comporte des nombres transparents. Toutefois, en grandissant, cette difficulté a tendance à s’estomper. Si l’apprentissage des nombres non transparents est juste une question de temps ou de pratique, pose-t-elle réellement un problème ? Oui, car même si beaucoup d’enfants les maîtrisent rapidement, d’autres ont du mal à s’en sortir. Par exemple, une étude a révélé que les enfants qui ont des difficultés avec les nombres écrits à l’âge de 7 ans sont plus susceptibles d’avoir des difficultés en mathématiques 3 ans plus tard [3]. Ces difficultés peuvent donc permettre de détecter les enfants qui ont besoin d’aide en mathématiques. Plus vite on les aidera, mieux ils s’en sortiront.
… Mais, les problèmes ressurgissent lorsqu’on essaie de faire des maths dans une autre langue !
De plus en plus de personnes voyagent ou vivent dans d’autres pays dont ils doivent apprendre la langue. Parfois, cette nouvelle langue a une manière particulière de désigner les nombres à plusieurs chiffres et ceux-ci doivent être appris par cœur. Cela peut poser de gros problèmes, notamment si tu viens de Pologne (aucune permutation requise) et que tu souhaites vivre en Allemagne (permutation requise). C’est notamment le cas de Krzysztof, l’un des auteurs de cet article. Chaque fois qu’il fait des courses et veut les payer, il s’embrouille. Quand la caissière lui dit « Neunundzwanzig euro, bitte ! » [« Neuf-et-vingt euros, s’il vous plaît ! »], la première question que Krzysztof se pose est : « Comment ai-je pu dépenser presque cent euros pour des courses que je compte consommer dans les 3 prochains jours ? » Il a beau savoir qu’il doit procéder par permutation et faire des recherches sur ce sujet, il lui faut toujours quelques instants pour se calmer et payer le bon montant.
Apprendre des nombres en lettres dans une nouvelle langue est un bon début, même si cela est déjà délicat. Il convient de noter toutefois que tu n’auras pas forcément pour autant envie de faire des mathématiques dans cette langue. Généralement, les gens préfèrent faire des maths dans une seule langue, et pas dans celle qu’ils viennent juste d’apprendre. Il est plus probable qu’ils privilégient leur langue maternelle ou celle avec laquelle ils ont appris les maths.
Conclusion
Nous utilisons chaque jour les nombres ainsi que leur désignation et pour beaucoup d’entre nous, ils sont faciles – du moins après suffisamment de pratique. Cependant, lorsqu’on les examine attentivement, il est intéressant de voir comment les langues diffèrent dans la désignation des nombres à plusieurs chiffres. Malgré ces différences, leur construction n’est pas hasardeuse mais obéit a des règles précises. Regarde de nouveau le jeu de la Figure 1. Maintenant que tu as appris les règles énoncées, vois si tu peux lire certains de ces nombres plus aisément. Un examen détaillé des nombres en lettres permet de comprendre pourquoi les enfants qui parlent une seule langue ont plus de difficultés en mathématiques que ceux qui en parlent deux. Il nous aide aussi à identifier de manière précoce les enfants ayant des difficultés en maths et à trouver des solutions pour les aider. Bien sûr, les règles de construction de ces nombres ne constituent pas le seul point essentiel pour l’apprentissage des mathématiques, mais elles sont une pièce déterminante du puzzle.
Glossaire
Système de numérotation indo-arabe: ↑ C’est un ensemble de symboles employés dans la plupart des pays pour écrire les nombres. Le Système de numérotation indo-arabe utilise exactement 10 symboles : 1, 2, 3, 4, 5, 6, 7, 8, 9, et 0. Ces dix symboles servent à écrire des nombres à un seul chiffre et nous les combinons pour obtenir des nombres à plusieurs chiffres.
La règle de la valeur de position: ↑ C’est une règle qui nous permet d’écrire autant de nombres que nous souhaitons avec les 10 symboles que nous connaissons déjà (1, 2, 3, 4, 5, 6, 7, 8, 9 et 0). Elle implique que la valeur d’un chiffre est connue lorsqu’on regarde sa position dans un nombre à plusieurs chiffres. Par exemple, dans 92, la valeur de 9 est 90 (9 × 10) et celle de 2 est 2 (2 × 1) alors que dans 29 c’est le contraire : la valeur de 9 est 9 (9 × 1) et celle de 2 est 20 (2 × 10). Par conséquent, 92 est différent de 29, même si les deux nombres sont le résultat d’une combinaison des mêmes chiffres.
Transparent: ↑ Transparent est le synonyme de clair ou bien structuré. Pour ce qui est de l’écriture en lettres, l’adjectif transparent est utilisé pour décrire les langues où les nombres se disent précisément en suivant la manière dont ils sont écris en chiffres. Les langues transparentes mettent clairement en lumière la règle de la valeur de position (par exemple, 97 = 9 × 10 + 7 = « neuf-dix-sept »).
Inversion des nombres: ↑ Dans certaines langues, l’ordre dans les nombres à deux chiffres est permuté. À titre d’exemple, plutôt que de dire quarante-deux pour 42, on dira deux-et-quarante. Cette permutation constitue l’inversion des nombres.
Conflit d’intérêts
Les auteurs déclarent que les travaux de recherche ont été menés en l’absence de toute relation commerciale ou financière pouvant être interprétée comme un potentiel conflit d’intérêts.
Remerciements
Nous remercions Ani, âgé de 11 ans, pour ses commentaires sur la première version du manuscrit. Nous remercions aussi tous ceux qui ont contribué à la traduction des articles de cette Collection afin de les rendre accessibles et compréhensibles aux enfants des pays non anglophones et la Fondation Jacobs pour avoir octroyé les fonds nécessaires pour cette traduction.
Déclaration d’utilisation des outils d’IA
Tout texte alternatif fourni avec les figures de cet article a été généré par Frontiers grâce à l’intelligence artificielle. Des efforts raisonnables ont été déployés pour garantir son exactitude, notamment par une relecture par les auteurs lorsque cela était possible. Si vous constatez des problémes, veuillez nous contacter.
Notes de bas de page
1. ↑ “Maths” est l’abréviation de mathématiques utilisée au Royaume-Uni. Aux États-Unis d’Amérique, on utilise “math”.
2. ↑ Le « × » dans 7 × 8 est un symbole de multiplication. Cependant, on utilise aussi « ⋅ » (7 ⋅ 8) ou « * » (7 * 8).
Références
[1] ↑ Moeller, K., Zuber, J., Olsen, N., Nuerk, H.-C., and Willmes, K. 2015. Intransparent German number words complicate transcoding–a translingual comparison with Japanese. Front. Psychol. 6:740. doi: 10.3389/fpsyg.2015.00740
[2] ↑ Zuber, J., Pixner, S., Moeller, K., and Nuerk, H.-C. 2009. On the language-specificity of basic number processing: transcoding in a language with inversion and its relation to working memory capacity. J. Exp. Child Psychol. 102:60–77. doi: 10.1016/j.jecp.2008.04.003
[3] ↑ Moeller, K., Pixner, S., Zuber, J., Kaufmann, L., and Nuerk, H.-C. 2011. Early place-value understanding as a precursor for later arithmetic performance–a longitudinal study on numerical development. Res. Dev. Disabil. 32:1837–51. doi: 10.1016/j.ridd.2011.03.012
