ملخص
يمكن أن يؤثر عليك أصدقاؤك بطرق لا تدركها، على طريقة تفكيرك وتصرفك وما تحبه وما تكرهه وما تشتريه وأدائك في المدرسة. ويقدّر العلماء أهمية المعلومات عن معارفك من الناس لأنه يمكن استخدامها لفهم كيفية انتشار الأفكار بل والأمراض في بعض الأحيان. ويمكن للعلماء بوجه عام وعلماء الرياضيات بوجه خاص استخدام البيانات والرياضيات المتقدمة لصياغة تخمينات مدروسة حول مدى احتمال حدوث شيء ما. على سبيل المثال، يمكننا التنبؤ باحتمال إقامة صداقة بينك وبين شخص آخر بالنظر إلى القليل من المعلومات فقط، مثل المدرسة التي تذهبان إليها وهواياتكما ومعارفكما من الناس. في هذا المقال، ستتعرّف على بعض الأدوات التي ستساعدك على أن تصبح عالمًا في الشبكات وتصيغ توقعات رياضية حول الصداقات.
هل يمكن للعلماء توقع نوعية أصدقائك؟
يقول المثل: لا يهم ما تعرف، بل مَن تعرف. يجمعك بأصدقائك على الأرجح الكثير من الأمور المشتركة. فهل يمكنك إعداد قائمة بها؟ ما الاهتمامات والسمات المشتركة بينك وأصدقائك؟ هل تذهبون إلى المدرسة نفسها أو تلعبون في الفريق نفسه؟ هل تعيشون في الحيّ نفسه أو المدينة نفسها؟ هل لديكم أصدقاء مشتركون؟ ستجيب بنعم في الغالب على بعض الأسئلة على الأقل فيما يخص كل واحد من أصدقائك المقربين. قد لا تكون مدركًا لاشتراكك مع أصدقائك أيضًا في كل أنواع المعلومات والمواقف والسلوكيات المتعلقة بالمدرسة. وجد العلماء أن الأشخاص المحيطين بك وما يعرفونه ويعتقدونه حول المدرسة وشكل سلوكهم، كل ذلك يمكن أن يؤثر على مستقبلك الدراسي [1]. بمعنى آخر، يؤثر أصدقاؤك على عاداتك وأدائك في المدرسة. على الجانب الآخر، يمكن أن يؤثر أداؤك في المدرسة على نوعية أصدقائك [2]. وقد اتضح أن علماء الاجتماع والرياضيات يمكنهم أيضًا إلى حد ما توقّع نوعية أصدقائك.
ما الشبكة الاجتماعية؟
يستخدم العلماء الدارسون للشبكات المعادلات الرياضية لإنشاء رسوم بيانية للسلوكيات وسمات العلاقات وقياسها، ومن أمثلة ذلك مَن تطلب منهم المساعدة ومدى قرب الأصدقاء إليك [3]. ويمكن تعريف الشبكة الاجتماعية على أنها شبكة من الصلات الشخصية يتبادل الناس فيها المعلومات والموارد. ويعتمد حجم المعلومات والموارد المتبادلة في أي شبكة على أنماط وجودة العلاقات داخل الشبكة [4]. إذا أردت معرفة المزيد حول علم الشبكات، يمكنك قراءة مقالة Frontiers for Young Minds هذه.
يمكننا أيضًا تصوّر الشبكات الاجتماعية بإنشاء الرسوم البيانية، حيث يتم تمثيل الأشخاص كدوائر ملونة تُسمى العُقد. ويمكن أن تمثل ألوان العُقد خصائص الأشخاص في الشبكة، مثل الصف الدراسي أو العمر أو الجنس. ويتم تمثيل الصلات بين الأشخاص (على سبيل المثال الصداقات) في شكل خطوط بين العُقد، واسمها ''الحواف'' (الشكل 1).
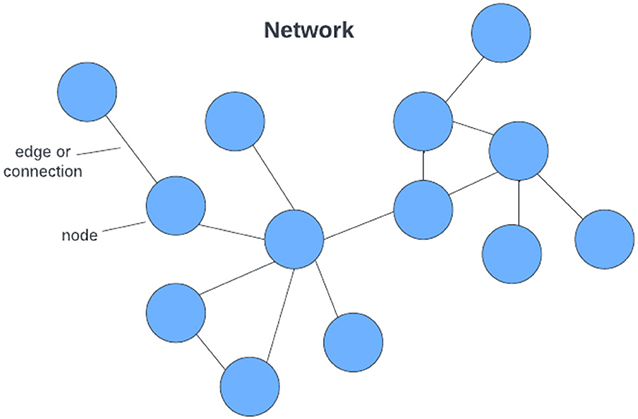
- شكل 1 - مثال على رسم بياني لشبكة اجتماعية:
- كل نقطة زرقاء هي عقدة تمثل طالبًا والخطوط بين الطلاب (الحواف) تشير إلى أنهم أصدقاء.
توقّع نوعية الأصدقاء باستخدام الرياضيات المتقدمة ونماذج الرسم البياني العشوائي الأسي (ERGM)
يُعدّ نموذج الرسم البياني العشوائي الأسي (ERGM) من أدوات الرياضيات المتقدمة التي تتوقع مدى احتمال ارتباط شخصين بصلة معينة بالاعتماد على خصائص شبكة ما. يقارن نموذج ERGM كل الصلات العشوائية المحتملة في شبكة ما لمعرفة مدى احتمال ارتباط شخصين بصلة محددة في مرحلة ما في المستقبل. إذًا في الأساس، يُعد نموذج ERGM أداة لتوقع الصلات بين الأشخاص.
باستخدام نموذجنا المبسط، يمكنك التوصل إلى توقعاتك على أساس خمسة أسئلة فحسب. هل يخطر ببالك شخصًا ما؟ رائع، لنجرّب الأمر.
ما مدى كثافة شبكتك؟
هل أنت منضم إلى فريق أو نادٍ رياضي يرتبط أغلب أعضائه بصداقة مع بعضهم؟ ستكون هذه شبكة كثيفة، وأغلب أفرادها الذين يُحتمل أن يرتبطوا بصداقة معًا هم أصدقاء في الواقع. توصف الكثافة بقيمة مئوية يتم حسابها على الشكل التالي: عدد الصلات الفعلية (الروابط) في مجموعة معينة (الشبكة) مقسومًا على كل الصلات المحتملة (الروابط) في المجموعة (الشبكة). على سبيل المثال، كلتا الشبكتين في الصورة أدناه (الشكل 2) لديهما 50 عقدة، ولكن الشبكة على اليمين لديها صلات أكبر كثيرًا (خطوط) بين العُقد ولذلك فهي أكثف.
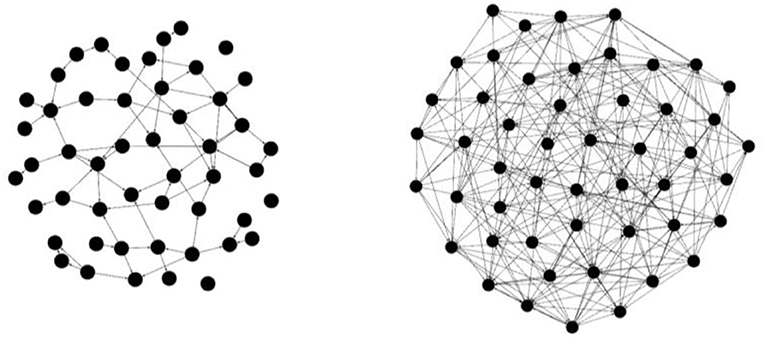
- شكل 2 - (اليسار) مثال على شبكة اجتماعية ذات روابط أقل كثافة.
- (اليمين) مثال على شبكة اجتماعية ذات روابط أعلى كثافة.
الكثافة مهمة في حاسبات ERGM لأنه يمكن أن تزيد أو تقل من احتمال ارتباط شخصين بصلة معينة في المستقبل. وفي الشبكات عالية الكثافة، سيكون احتمال نشوء صلة بين فردين أكبر كثيرًا، أي أنه في الشبكات عالية الكثافة، يزيد كثيرًا احتمال ارتباط أي شخصين في الشبكة بصلة محددة في النهاية.
كم عدد الأصدقاء المشتركين بينكم؟
هل يرتبط أي من أصدقائك بصداقة ببعضهم أيضًا؟ يُسمى هذا التثليث، وهو ارتباط الأشخاص بصداقة مع أصدقاء أصدقائهم. سترتبط على الأرجح بصداقة مع أصدقائهم لهذا السبب. في الرسوم البيانية للشبكات، تتسبب هذه الصلات (الخطوط) في ظهور أشكال مثلثة، ولذلك نسمي ذلك التثليث. وعندما تكثر المثلثات في رسم بياني لشبكة، تزيد قيمة التثليث. وتزيد قيمة التثليث العالية من احتمال ارتباط شخصين بصلة معينة في النهاية، على عكس قيمة التثليث المنخفضة.
هل يعتبرك أصدقاؤك صديقًا؟
لنفترض أننا طلبنا منك تحديد أعز أصدقائك، فهل يعتبرك هذا الشخص أقرب صديق له أيضًا؟ إذا كانت الإجابة نعم، نسمي ذلك المعاملة بالمثل. إليك مثال آخر: في شبكة فصل مدرسي، قد يعتبرك طالب معين بين الأشخاص الذين يقصدهم لطلب المساعدة، وتعتبره أنت أيضًا كذلك. في كلتا الحالتين، ''يرسل'' الأشخاص صلات إلى بعضهم. ولأن المعاملة بالمثل تدل على كثافة الصلات في الشبكة، فهي قيمة مهمة لحاسبات نموذج ERGM. وكما هي الحال مع الكثافة والتثليث، تزيد القيمة العالية للمعاملة بالمثل من احتمال ارتباط شخصين بصلة محددة في النهاية.
هل تقصد أصدقاءك لطلب النصيحة؟
إذا طلبنا منك إنشاء قائمة بأصدقائك ثم قائمة بالأشخاص الذين تقصدهم لمساعدتك في الفروض الدراسية وقائمة أخرى بالأشخاص الذين تقصدهم لطلب الدعم في وقت الضيق، يُحتمل أن يتواجد صديق واحد على الأقل في أكثر من قائمة من هذه القوائم. وفقًا لعلماء الشبكات، لديك أنواع كثيرة من الصلات (الحواف) مع ذلك الصديق. وعندما تتعدد أنواع الصلات (الحواف) مع فرد ما، يُسمى ذلك بظاهرة تأثير الحافة. في الأساس، يعني مصطلح ''تأثير الحافة'' أنك إذا قضيت الكثير من الوقت مع صديق ما، من المحتمل أن تكون مرتبطًا به بعدة طرق. وكلما زادت تأثيرات الحافة في شبكة ما، زاد احتمال ارتباط شخصين بصلة معينة في نهاية الأمر، ما يجعل ذلك قيمة أخرى مهمة في حاسبات نموذج ERGM.
هل تتشاركون في خصائص؟
هل سمعت من قبل مقولة ''الطيور على أشكالها تقع''؟ هل تلاحظ أنك وأصدقاءك تتشاركون في الغالب فيما تحبونه وتكرهونه وفي الهوايات، بل والاعتقادات؟ يُسمى ذلك الهموفيليا ويحدث عندما يرتبط الناس بصلات مع آخرين يشبهونهم. إذًا، عندما يزيد مقدار الهموفيليا في شبكة ما، ينشئ الناس في الغالب الكثير من الصلات. وعلى غرار الخصائص الثلاث الأخرى في الشبكات (الكثافة والتثليث والمعاملة بالمثل وتأثير الحافة)، يمكن أن يزيد مقدار الهموفيليا أو يقل من احتمال ارتباط شخصين بصلة ما في النهاية، ولذلك يود علماء الشبكات إدراجه في حاسبات ERGM.
توقعّ الأصدقاء: كيف يتم الأمر؟
يتم التعبير عن تقديرات نماذج ERGM في شكل وحدات من ''الأرجحية اللوغاريتمية'' (لوغاريتم نسبة أرجحية). ويستخدم علماء الرياضيات الأرجحية اللوغاريتمية لأنها أداة سهلة لدمج متغيرات الاحتمال.
الأرجحية هي احتمال النجاح (الفوز في لعبة بينك وبيني) مقابل احتمال الفشل (خسارة اللعبة). على سبيل المثال، لنفترض أن هناك احتمال 1 من 4 (0.25) أن تفوز (تنجح) واحتمال 3 من 4 (0.75) ألا تفوز (تفشل). لحساب قيمة الأرجحية الخاصة بفوزك، نقسم احتمال النجاح (0.25) على احتمال الفشل ،(0.75) فنحصل على (0.25/0.75).
لنفترض الآن أنني لست بارعًا مثلك في اللعبة، إذًا احتمال أن أفوز يعادل (0.10) واحتمال ألا أفوز يعادل (0.9). لحساب قيمة الأرجحية الخاصة بفوزي، نقسم احتمال النجاح (0.10) على احتمال الفشل (0.9)، فنحصل على (0.10/0.9).
وبعد ذلك لمقارنة احتمال فوزي وفوزك، علينا دمج قيمتي الأرجحية من خلال إنشاء نسبة، وهذا بقسمة قيمة الأرجحية الخاصة بك على القيمة الخاصة بي. تصاغ نسبة الأرجحية بين احتمال فوزنا باللعبة كالتالي، (0.25/0.75)/(0.1/0.9) ويتم تبسيطها إلى 3، ما يعني أن أرجحية فوزك أكبر 3 مرات من أرجحية فوزي.
قد تلاحظ أن نسب الأرجحية غير متناظرة. على خط أعداد عادي، يكون أقل رقم هو لانهاية سالبة وأكبر رقم هو لانهاية موجبة والرقم ''الأوسط'' هو الصفر. ولكن في نسب الأرجحية، أقل رقم محتمل هو الصفر وأعلى رقم محتمل هو لانهاية موجبة والرقم ''الأوسط'' هو واحد.
فكّر في ذلك كالتالي: إذا كان احتمال أن أهزمك في التنس أكبر بمرتين، فإن احتمال هزيمتك لي هي النصف. وهما متساويان من حيث النسبة ولكنهما (2 و0.5) من الناحية العددية عبارة عن مسافتين مختلفتين من 1 على خط الأعداد، ويعني الرقم 1 أن احتمالات هزيمتنا لبعضنا متساوية. نحسب بعد ذلك لوغاريتم نسبة الأرجحية. تتميز الدالة اللوغاريتمية بعدة أشياء، ولكن الميزة الأكثر صلة بموضوعنا هي أن لوغاريتم 1 يساوي 0 ولموجب x، تكون المعادلة: log(x) = −log(1/x). على سبيل المثال، لوغاريتم 2 يساوي 0.69 ولوغاريتم 1/2 يساوي−0.69. إذًا، عند حساب نسبة الأرجحية على أساس أنها احتمال فوزي مقابل احتمال فوزك أو العكس وهذا من خلال حساب اللوغاريتم، سنحصل على الأرقام نفسها. والاختلاف الوحيد هو علامة الموجب أو السالب، أي أنهما مسافتان متساويتان من الرقم 0 على خط الأعداد.
إذًا، عند حساب لوغاريتم الأرجحية، تتحول الاحتمالات المتساوية إلى 0، وينتج تقدير متناظر للأرجحية. ويستخدم علماء الرياضيات الأرجحية اللوغاريتمية لأنها أداة سهلة لدمج عدة نسب أرجحية، وهذا ما ستطبقه حاسبتنا التفاعلية. ولكن في حالتنا، يمكننا أن نستخدم ''النقاط'' بدلاً من الأرجحية اللوغاريتمية.
استخدام الحاسبة التفاعلية
اخترنا قيمًا محددة للحاسبة التفاعلية (النموذج) أدناه على أساس النواتج العادية للشبكة الاجتماعية. على سبيل المثال، فإن أرجحية نشوء صداقة بين الأشخاص الذين يجمعهم أصدقاء مشتركون تكون مرتفعة (الاحتمالات أكبر ثلاث مرات في هذه الحالة) حتى في الشبكات الأقل كثافة عادةً، مثل شبكات الصداقة.
يمكن تغيير الأرقام في الحاسبة التفاعلية (النموذج) أدناه (الشكل 3) حسب أنواع التشابه التي يعتقد واضعو النموذج أنها أكبر أهمية بالنسبة لتكوين الصداقة في الشبكة المحددة. والاختيارات مثل ''4 نقاط لتبادل النصيحة، ونقطة واحدة لنفس الهوية الجنسية'' هي مجرد اختيارات وليست قواعد ثابتة. ففي كثير من الأحيان، تعدّل الرياضيات التطبيقية أي نموذج لتجعله يمثل الواقع بصورة أدق. غير أنه وفقًا للبحث، ثبت أن أنواعًا معينة من التشابه ساهمت أكثر في تكوّن الصداقة في شبكات المدارس الكبيرة (ولذلك أدرجنا بعضها فيما يلي). على سبيل المثال، إذا كان لديكما أصدقاء مشتركون، فاحتمالات تكوّن الصداقة بينكما كبيرة وإذا كنت تطلب النصيحة من شخص ما في المدرسة، فهناك احتمال كبير أن تنشأ صداقة بينكما. ومع ذلك، فالقيم الفعلية افتراضية.
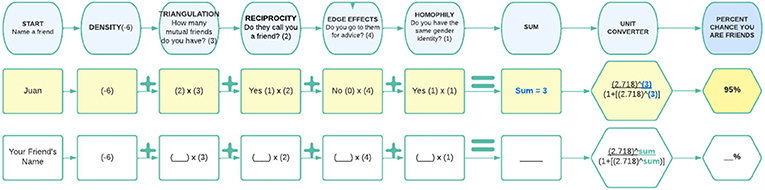
- شكل 3 - (الصف العلوي) مثال على كيفية استخدام الحاسبة التفاعلية لتحديد النسبة المئوية لاحتمال تكوّن صداقة بينك وبين ''سامي''.
- (الصف السفلي) الحاسبة التفاعلية لتحديد النسبة المئوية لاحتمال تكوّن صداقة بينك وبين شخص آخر.
''نقاط'' الصداقة
تخيّل شخصين يذهبان إلى المدرسة نفسها، وهما أنا وأنت. في الغالب، لا تكون شبكات الصداقة في المدارس الكبيرة كثيفة للغاية، ولذلك سنبدأ بافتراض كثافة شبكة (منخفضة)، وبهذا يكون لدينا سالب 6 نقاط. لنفترض أن لدينا صديقين مشتركين (التثليث)، فنستعيد 6 نقاط. وكلانا يعتبر الآخر صديقًا (المعاملة بالمثل)، ما يضيف نقطتين إلى المجموع. ولكن لا يطلب أحد منا النصيحة من الآخر (تأثيرات الحافة)، فلا نحصل إذًا على نقاط هذه الميزة. والآن لنفترض أيضًا أننا نتشارك الهوية الجنسية نفسها (الهموفيليا)، فنحصل إذًا على نقطة. عند حساب الإجمالي، يكون كالتالي: −6 + 6 + 2 + 0 + 1 = 3.
حساب الأرجحية
هذا المجموع البالغ 3 لنقاط الصداقة يمثل الأرجحية اللوغاريتمية لاحتمال تكوّن الصداقة بيننا. ولتحويل ذلك إلى رقم مفهوم (النسبة المئوية للاحتمال)، علينا حساب عكس اللوغاريتم. وهذا ما تقوم به الصيغة في الحاسبة التفاعلية بالضبط، فهي تحوّل الأرجحية اللوغاريتمية إلى نسبة مئوية للاحتمال. للقيام بذلك، نرفع عدد أويلر (ثابت رياضي يساوي تقريبًا 2.718) إلى أس مجموع نقاط الصداقة، مقسومًا على 1 زائد عدد أويلر مرفوعًا إلى أس مجموع نقاط الصداقة. وعند وضع الأعداد الخاصة بمثالنا في الصيغة التالية، تكون النتيجة 0.95، أي احتمال بنسبة 95% أن نتحوّل إلى أصدقاء.
دورك الآن
بناءً على إجاباتك عن الأسئلة أدناه، ستتغير قيمة نقاط نموذج ERGM. وسنحوّل قيمة النقاط إلى نسبة مئوية عند انتهائك لجعلها أسهل في التطبيق على الحالات الواقعية. إذا كانت النسبة المئوية عالية (أكبر من 50%)، فالصداقة محتملة. إذا كانت النسبة المئوية منخفضة (أقل من 50%)، فالصداقة غير محتملة.
والآن يمكنك استخدام حاسبة نموذج ERGM التفاعلية وحدك لمعرفة احتمالات نشوء صداقة بينك وبين شخص تعرفه في الواقع.
المستوى المتقدم
إذا أردت تجربة شيء أكثر تقدمًا بعض الشيء، فجرّب اللعب بالنموذج لتغيير هذه الأرقام ورؤية النتيجة، أيّ القيم تؤدي إلى أكثر الشبكات الفعلية دقة؟ هذه هي الطريقة التي تعمل بها نماذج الحياة الواقعية.
تجدر الإشارة إلى أن مثالنا حول شبكة الصداقة في إطار مدرسة كاملة ليس كثيفًا بدرجة كبيرة. ولكن لنفترض أنك تريد تجربة ذلك مرة أخرى مع شبكة أصغر وأكبر كثافة مثل نادي معين متخصص في أشياء غير دراسية مثل فرقة موسيقية أو نادي خطابة ومناظرات. يصعب التعرّف على كل شخص في مدرستك، ناهيك عن إقامة صداقة مع الجميع. ولكن يسهل أكثر التعرّف على كل الأشخاص في مجموعة صغيرة وتكوين صداقة معهم. وفي حالة المجموعة أو النادي الصغير، من المحتمل أن ينتج معامل كثافة موجب في الحاسبة (مثل 3 أو 6 نقاط بدلاً من سالب 6). يمكنك أيضًا تقدير الكثافة الفعلية لشبكة صغيرة من خلال حساب صلات الصداقة الفعلية الحالية في المجموعة مقسومة على إجمالي عدد الصلات المحتملة بين الأفراد في المجموعة.
وبعد أن عرفت كيفية القيام بذلك، حاول رسم خريطة لشبكتك الاجتماعية واستخدم قيم الكثافة في الحاسبة. ستلاحظ أنه كلما زادت الكثافة، زادت النسبة المئوية لاحتمال تكوّن الصداقات. وهكذا تطبق بنفسك علم الشبكات.
الخاتمة
قد تكون تتساءل الآن عن السبب وراء رغبة أي شخص في توقع نوعية أصدقائي. حسنًا، هناك استخدامات كثيرة لهذا النوع من المعلومات. فالقدرة على توقع صلاتك الاجتماعية بدقة يفيد في العثور على ''أصدقاء'' لك على تطبيقات التواصل الاجتماعي، كما أنها فرصة غانمة لبائعي التجزئة على الإنترنت أو مسؤولي الحملات السياسية أو أولئك الساعين وراء نشر المعلومات الزائفة على سبيل المثال لا الحصر. لفهم ذلك، تصوّر أنه لو كان التطبيق مجانيًا، فأنت وصلاتك الاجتماعية (شبكاتك الاجتماعية) المنتج. تتلاعب عمليات التصيد الاحتيالي أيضًا بشبكاتك الاجتماعية لنشر فيروسات الكمبيوتر، حيث يتم تنزيل كل جهات اتصالك وإرسال فيروس إليهم كما لو كنت أنت مَن ترسل الرسالة الإلكترونية. ويستخدم علماء الأوبئة نماذج توقع الشبكات الاجتماعية الكبيرة وتتبع مخالطي المرضى لتحديد كيفية تقديم أفضل حماية لك من انتشار المرض المعدي.
ولكن الأصدقاء لا يتبادلون الجراثيم وفيروسات الكمبيوتر فحسب، بل الأفكار والمواقف تجاه العالم، ويؤثرون في سلوكيات بعضهم، بما في ذلك التمارين والاهتمامات والتغيب عن المدرسة بدون أعذار والنتائج الدراسية. لا نقصد بذلك أنه لا بد أن يكون أصدقاؤك الأوائل في الفصل حتى تنجح أنت في الحياة، ولكن بناءً على الرياضيات، من الأفضل بالطبع أن تبقى على صلة بأصدقائك المتفوقين في المدرسة. ولا تنس أن جودة العلاقات مهمة أيضًا. وهكذا من منطلق الرياضيات، أنت تعرف الآن أن نوعية معارفك من الأشخاص مهمة.
مسرد للمصطلحات
الشبكة الاجتماعية (SOCIAL NETWORK): ↑ مجموعة من الأشخاص (يُطلق عليهم العُقد) والصلات (الروابط أو الحواف) بين هؤلاء الأشخاص (العُقد).
العُقد (NODES): ↑ دوائر تمثل الأفراد في الرسوم البيانية للشبكات الاجتماعية.
الحواف (EDGES): ↑ خطوط تربط العُقد (الأشخاص) في الرسوم البيانية للشبكات الاجتماعية.
نموذج الرسم البياني العشوائي الأسي (ERGM): ↑ أداة من أدوات الرياضيات المتقدمة يتم استخدامها لتوقع الصلات بين الأشخاص في الشبكات الاجتماعية.
الكثافة (DENSITY): ↑ النسبة المئوية للصلات في شبكة اجتماعية.
التثليث (TRIANGULATION): ↑ ميل الأشخاص إلى الدخول في صداقة مع أصدقاء أصدقائهم.
المعاملة بالمثل (RECIPROCITY): ↑ ميل الأشخاص إلى ''رد'' الصلات (الروابط) إلى الأشخاص الذين بادروهم بإرسال صلة (رابط).
الهموفيليا (HOMOPHILY): ↑ ميل الأشخاص إلى إقامة صداقة مع الأشخاص الذين يشبهونهم.
إقرار تضارب المصالح
يعلن المؤلفون أن البحث قد أُجري في غياب أي علاقات تجارية أو مالية يمكن تفسيرها على أنها تضارب محتمل في المصالح.
المراجع
[1] ↑ Bourdieu, P., and Passeron, J. C. 1977. Reproduction in Education, Society and Culture. New York, NY: Oxford University Press.
[2] ↑ Ito, M. 2010. Hanging Out, Messing Around, and Geeking Out: Kids Living and Learning With New Media. Cambridge, MA: The MIT Press.
[3] ↑ Lin, N. 1999. Building a network theory of social capital. Connections 22: 28–51.
[4] ↑ Daly, A. J., Moolenaar, N. M., Bolivar, J. M., and Burke, P. 2010. Relationships in reform: the role of teachers’ social networks. J. Educ. Administr. 48:359–91. doi: 10.1108/09578231011041062