ملخص
الرياضيات جزء لا يتجزأ من الطب. فجميع الرسوم البيانية والمعادلات والإحصاءات والرياضيات العامة التي نتعلمها في المدرسة تساعدنا في فهم الجوانب المهمة للطب البشري والبيطري وعلم الأحياء والعلوم بصفة عامة. ومن المعتقدات الشائعة لدى الناس أن علم الأحياء والكيمياء من العلوم المهمة للأطباء وطواقم التمريض والقابلات والعلماء وجميع الأشخاص الآخرين الذين يشغلون وظائف لها صلة بالطب والرعاية الصحية، لكنهم يغفلون عن الرياضيات التي لها أهمية حيوية أيضًا في مجال الطب. لذلك، إذا كنت تحلم بأن تصبح طبيبًا أو تبتكر تقنيات طبية أو كنت مريضًا كل ما تريده هو فهم العلاجات التي تتناولها، فإن فهم الرياضيات التي ينطوي عليها الطب أمر لا غنى عنه. ونحن في هذا المقال نتناول بالبحث كيف نتحقق من إصابة الشخص بمرض مثل فيروس كورونا أو بأمراض القلب، وكيف نتنبأ بعدد الأشخاص الذين سيُصابون بأمراض مختلفة ونقيس هذا العدد، وكيف يمكننا استخدام الرياضيات لعلاج المرضى ومنع انتشار الأمراض المعدية. يدرك الناس عمومًا أهمية الإلمام بالعلوم مثل الأحياء والكيمياء للوظائف في المجال الطبي، ولكن لا يعرف الكثير منهم أن الرياضيات لا تقل أهمية أيضًا لمعظم هذه الوظائف. لهذا، سيتطرق هذا المقال لبعض استخدامات الرياضيات في الطب. فإذا كنت تطمح إلى أن تصبح طبيبًا أو جراحًا بيطريًا أو ممرضًا أو قابلة أو عالمًا طبيًا أو أن تشغل أي وظيفة تتعلق بعلاج الأشخاص والحيوانات، أو حتى إذا كان كل ما تريده هو أن تكون مريضًا ملمًا بطبيعة مرضك وبما تتلقاه من علاج، فلا بد أن تعلم أن معرفتك بالرياضيات لها أهمية كبيرة!
دور الرياضيات في دراسة توزيع الأمراض وانتشارها
علماء الأوبئة هم عاملون في المجال الطبي يمارسون أعمالًا تتعلق بعلم الأوبئة، وهو دراسة توزيع الأمراض والاضطرابات مثل فيروس كورونا وشلل الأطفال والربو وأمراض القلب والسرطان وانتشارها والوقاية منها.
ويجب أن يعرف علماء الأوبئة مستوى العدوى الموجودة ليفهموا مدى خطورة المرض المُعدي. أما معدل الوقوع فهو عدد حالات الإصابة الجديدة بالمرض ضمن مجموعة من السكان في غضون فترة زمنية معينة (سنويًا أو شهريًا أو أسبوعيًا أو يوميًا). وعلاوةً على عدد الحالات الجديدة، فإن معرفة كيفية انتشار المرض بالفعل لهي أمر بالغ الأهمية. ويبين الانتشار نسبة السكان المصابين بالمرض في أي وقت معين، بحيث يمكننا تقديم يد العون للأشخاص الذين بحاجة للمساعدة أكثر من غيرهم. فمثلًا، إذا أُصيب 500 شخص في بلدة يبلغ عدد سكانها 1000 نسمة (50%) بفيروس كورونا، فهذا أخطر من إصابة 500 حالة في مدينة يبلغ عدد سكانها 20.000 نسمة (2.5%)، على الرغم من تماثل عدد المصابين.
ربما سمعت في الآونة الأخيرة عن رقم يُسمى عدد التكاثر R0 (يُنطق في اللغة الإنكليزية «آر نوت»). عدد التكاثر R0 يُسمى أيضًا بمعدل التكاثر الأساسي لكائن مُعدٍ (مثل الحصبة أو فيروس كورونا) ويعني متوسط عدد الحالات التي تسببها حالة واحدة حالية (الأشكال من 1A إلى 1C). ويسمح عدد التكاثر R0 لعلماء الأوبئة بفهم كيفية انتقال مرض من شخصٍ لآخر؛ حيث يعني عدد التكاثر R0 أقل من 1 أن المصاب سينقل العدوى لأقل من شخص آخر -في المتوسط- في حين إذا كان عدد التكاثر R0 أكثر من 1، فسيعني هذا أن سرعة انتشار المرض ستكون أكبر بكثير. وقد لا يبدو عدد التكاثر 3 R0 سيئًا، ولكن إذا نقل مصاب واحد العدوى إلى ثلاثة آخرين، الذين نقلوها بدورهم إلى 3 آخرين، فسيؤدي هذا بسرعة إلى إصابة 27 شخصًا بالعدوى (شكل 1D). وهذا ما يُسمى بالنمو الأُسي، وستزداد أعداد الحالات الجديدة بصورة أسرع وأسرع، ما لم نقلل عدد التكاثر R0 وننجح في وقف انتشار المرض (شكل 1E). يمكنك قراءة المزيد عن هذا في كتاب ديزيز ديتكتيف: الاستفادة من الرياضيات في التنبؤ بانتشار الأمراض المُعدية [1]. يتأثر عدد التكاثر R0 بالكثافة السكانية وعدد الأشخاص المُعرضين للخطر ومدى مخالطة الأشخاص بعضهم بعضًا ومدى عدوى المرض.
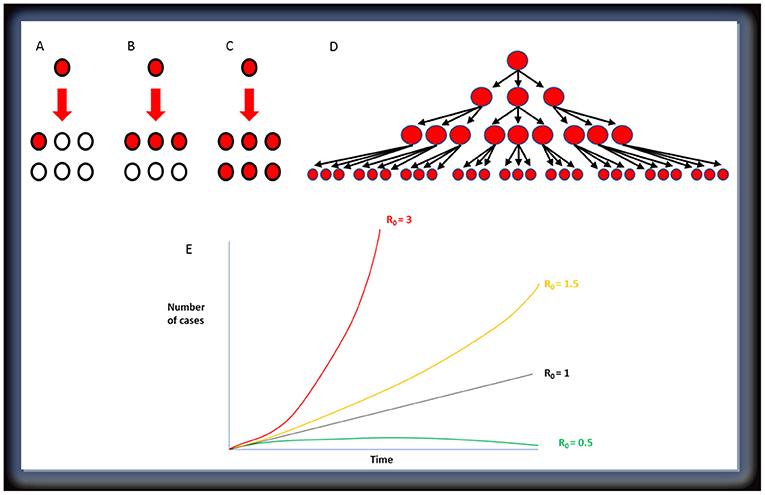
- شكل 1 - تمثل قيمة عدد التكاثر R0 عدد الأشخاص المُرجح أن تتنقل إليهم العدوى من الشخص المصاب.
- يظهر الأشخاص المصابون باللون الأحمر والأشخاص غير المصابين باللون الأبيض. (A) عندما يكون عدد التكاثر R0 = 1، ينقل شخص 1 العدوى لشخص 1 آخر. (B) عندما يكون عدد التكاثر R0 = 3، ينقل شخص 1 العدوى لثلاثة أشخاص آخرين. (C) عندما يكون عدد التكاثر R0 = 6، ينقل شخص 1 العدوى لستة أشخاص آخرين. (D) انتشار مرض بعدد تكاثر R0 3. (E) يرتفع عدد الحالات بوتيرة أسرع حتى عند وجود زيادات طفيفة في عدد التكاثر R0.
استخدام الرياضيات لتشخيص الحالات الطبية والأمراض
قبل أن نحسب عدد التكاثر 0R، علينا تحديد عدد الأشخاص الذين أُصيبوا فعلًا بالمرض أو الحالة الصحية. وتساعدنا الرياضيات في التأكد من تحديدنا للمشكلات الطبية وتشخيصها بطريقة صحيحة.
ويُطلق على فحص المرض مثل أمراض القلب أو مرض السكري الفحص التشخيصي، ويتضمن قياس كميات مواد معينة في عينات الدم أو أنواع أخرى من العينات. وعند فحص العينات، قد نحصل على مجموعة من النتائج:
• إيجابية صحيحة: نتيجة إيجابية مع وجود المرض
• إيجابية خاطئة: نتيجة إيجابية على الرغم من عدم وجود المرض
• سلبية صحيحة: نتيجة سلبية مع عدم وجود المرض
• سلبية خاطئة: نتيجة سلبية على الرغم من وجود المرض
دقة التشخيص هي قياس مدى جودة الفحص التشخيصي في معرفة الفرق بين الأصحاء والمرضى. وتُحسب باستخدام هذه المعادلة:

غير أن دقة التشخيص لا تظهر الصورة كاملة، ومن هنا تتجلى الحاجة أيضًا إلى مقاييس الحساسية والنوعية [2]. وتكمن حساسية الفحص التشخيصي في قدرته على تحديد النتائج الإيجابية الصحيحة بطريقة سليمة، في حين تكمن نوعية الفحص التشخيصي في قدرته على تحديد النتائج السلبية الصحيحة:

تعني النتيجة السلبية في فحص تبلغ نسبة حساسيته 100% أن المريض قطعًا ليس مصابًا بالمرض. بيد أن النتيجة الإيجابية في فحص ذي حساسية عالية لا تعني أن المرض موجود. وهنا تظهر فائدة النوعية؛ حيث تفيد النتيجة الإيجابية في فحص ذي حساسية عالية في تأكيد المرض. والوضع المثالي هو أن تكون الفحوصات التشخيصية حساسة ونوعية للغاية، ولكننا في بعض الأحيان لا نستطيع الحصول على كلتا الصفتين.
فمن المستحب أن تكون الفحوصات التشخيصية دقيقة وأن تكون على درجة عالية من الإحكام؛ حيث يشير الإحكام إلى قدرة الفحص على تحقيق نتائج موثوقة في كل مرة نستخدمه فيها. ويُحسب الإحكام باستخدام المعادلة التالية:

ونستخدم الرماية كمثال في شكل 2 لتوضيح هذه المفاهيم.
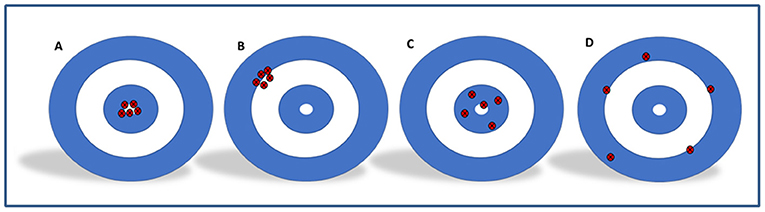
- شكل 2 - تساعدنا الرماية في فهم دقة التشخيص وإحكامه.
- تخيل أن نقطة الهدف هي التشخيص الفعلي للمريض، في حين أن النقاط الحمراء هي القِيَم التي تعطيها الفحوصات. (A) تتجمع الأسهم معًا وبالقرب من نقطة الهدف، لذلك يكون الفحص دقيقًا ومحكمًا. (B) تتجمع الأسهم معًا، لذلك يكون الفحص محكمًا، ولكن ليس بالقرب من نقطة الهدف، لذا فهو ليس دقيقًا. (C) جميع الأسهم بالقرب من نقطة الهدف ولكنها غير متجمعة، لذلك فالفحص دقيق ولكنه ليس محكمًا. (D) الأسهم منتشرة في كل مكان، لذلك فالفحص ليس دقيقًا ولا محكمًا.
دور الرياضيات في أمراض القلب
يُستخدم تخطيط كهربية القلب في مراقبة العديد من الناس عندما يُشتبه في تعرضهم لمشكلة قلبية أو عندما يكون تعرضهم لهذه المشكلة أمرًا معروفًا أو إذا كانوا مصابين بوعكة صحية من نوعٍ آخر. فيقيس تخطيط كهربية القلب حجم الإشارات الكهربائية في القلب وإيقاعها من خلال أقطاب كهربائية تُوضع على صدر المريض وذراعيه وساقيه. ويمكن بعد ذلك تخطيط هذه المعلومات على ورقة رسم بياني (شكل 3A). ويكون للرسم البياني المستمد من تخطيط كهربية القلب شكلًا مميزًا، مع تخصيص أحرف للمستويات الأعلى والأدنى المحددة؛ حيث تمثل الموجة P انقباض الأذينين (الحجرتين الموجودتين في الجزء العلوي من القلب). ويمكنكم الاطلاع على المزيد في المقال الذي يحمل عنوان «علاج القلب المنكسر: علم الوراثة في أمراض القلب» [3]. ويوضح مركب QRS انقباض البطينين (الجزأين السفليين من القلب). ويرجع كِبَر حجم الموجة R إلى أن البطينين هما الجزء الأكبر من القلب. وتوضح الموجة T الجزء الأخير من الدورة. ويمكن تحليل الأجزاء المختلفة للرسم البياني المستمد من تخطيط كهربية القلب لفهم ما إذا كان القلب يؤدي وظائفه كما ينبغي.
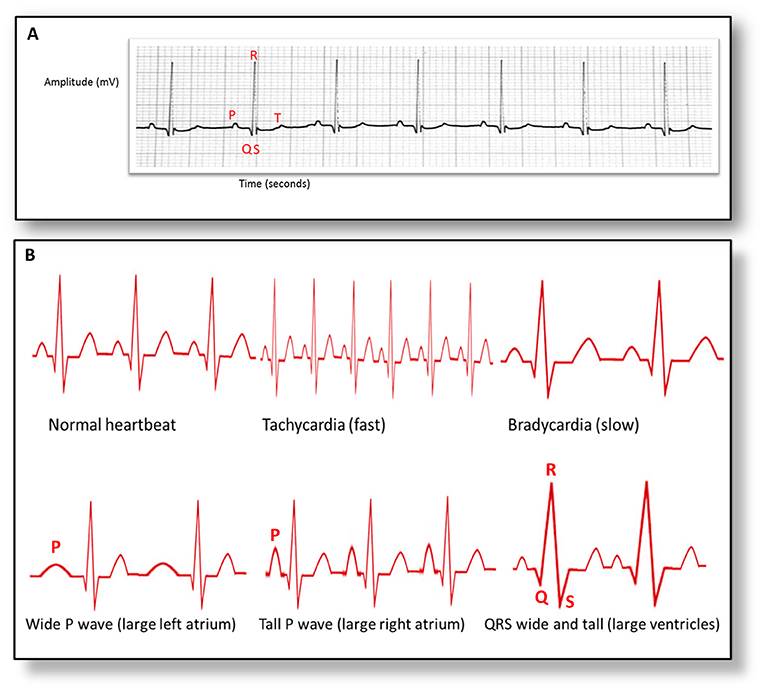
- شكل 3 - مخطط كهربية القلب (A) تمثل الأحرف المراحل المختلفة لدورة ضربات القلب.
- تُقاس المسافة بين موجتي R وتُحول إلى زمن لتحديد معدل ضربات القلب. فمثلًا، إذا كانت المسافة بين موجتي R هي 12.5 مم وكل مم يمثل 0.04 ثانية، فإن 12.5 × 0.04 = 0.5 ثانية بين ضربات القلب. وبما أن معدل ضربات القلب يُحسب على أنه عدد النبضات في الدقيقة، إذن 60 ثانية/0.5 = 120 نبضة في الدقيقة. (B) يمكن استخدام مخطط كهربية القلب لتشخيص اضطرابات القلب المختلفة، استنادًا إلى شكل الموجات وتباعدها.
فإذا كان شكل هذه الموجات أو توقيتها غير عاديين، فقد يعني هذا أن القلب يعمل بصورة غير طبيعية (شكل 3B).
وتوضح الفجوة بين موجات R معدل ضربات القلب. ويُطلق على معدل ضربات القلب السريع تسرع القلب، في حين يُطلق على معدل ضربات القلب البطيء بطء القلب. وقد يهدد الاضطرابان حياة الأفراد. فقد تعني موجة P العريضة بصورة غير عادية أن الأذين الأيسر متضخم، في حين قد تعني موجة P الأطول من المعتاد أن الأذين الأيمن متضخم. وقد يعود الشذوذ في الموجة T إلى مجموعة متنوعة من الأسباب، وهو شائع للغاية، ولا يؤدي دائمًا إلى وقوع مشاكل كبيرة. أما إذا كان المركب QRS عريضًا وطويلًا، فقد يكون البطينان متضخمين. ويُعرف هذا باسم تضخم القلب، وقد يكون مؤشرًا على فشل القلب أو إصابة أنسجة القلب أو ارتفاع ضغط الدم.
الاستخدامات الأخرى للرياضيات في الطب
قد يرغب أطباء القلب وأنواع أخرى من الأطباء في إلقاء نظرة على بنية القلب أو الأوعية الدموية أو الأعضاء الأخرى. وثمة عدة أساليب مستخدمة للتصوير داخل الجسم، منها الأشعة السينية والتصوير المقطعي بالحاسوب والموجات فوق الصوتية والتصوير بالرنين المغناطيسي [4]. وتحتاج جميع أساليب التصوير المذكورة إلى الرياضيات، ويجب أن تكون القياسات دقيقة، فلا مجال للخطأ في الطب.
وفور تشخيص حالة طبية، يجب مراقبة حالة المرضى وإعطاءهم الأدوية بطريقة صحيحة. ويعتمد حساب جرعات الأدوية على الرياضيات، مثل الجمع والكسور والمعادلات الجبرية، وهذه العمليات الحسابية بالغة الأهمية لأن جرعة الدواء التي قد تساعد البالغين قد تؤذي الأطفال، في حين قد تكون الجرعة المناسبة للأطفال غير كافية لمساعدة البالغين. ناهيك عن ضرورة إعطاء العديد من الأدوية لكل كيلوغرام من وزن الجسم.
وإذا كان المريض بحاجة إلى جراحة، فسيكون من الضروري حضور طاقم طبي لفحص ضغط دم المريض وحساب مستويات الأكسجين ومراقبة درجة حرارة الجسم ومعدل التنفس وإعطاء الجرعات الصحيحة من التخدير والسوائل. ولمزيد من المعلومات عن التخدير، انظر مقال «ما هو التخدير»؟ [5]. ويمكن لهذا الطاقم الطبي تحديد ما إذا كانت حالة المريض تتحسن أم تتدهور، وما الذي يحتاج إليه المريض أثناء العلاج من خلال إعداد الرسوم البيانية والمعادلات.
الخاتمة
تتجلى الأهمية البالغة للرياضيات في الطب البشري والبيطري في عدة جوانب. فقد يريد العاملون في المجال الطبي حساب مخاطر انتشار المرض، أو جرعة الدواء التي يجب إعطاؤها، أو سرعة ضربات القلب، أو تحديد ما إذا كانت حالة المريض تتحسن أم تسوء. لذا، في المرة القادمة التي تجري فيها بعض العمليات الحسابية، فكّر في مدى أهميتها واستخداماتها المفيدة للأطباء وطواقم التمريض والأطباء البيطريين والعلماء والأشخاص الآخرين الذين أخذوا على عاتقهم مهمة الحفاظ على صحتنا. وإذا كنت تفكر في العمل في إحدى هذه الوظائف في المستقبل، فتذكّر أن حصص الرياضيات لا تقل أهمية عن حصص العلوم!
إقرار
تمكننا من إنجاز جزء من هذا العمل بفضل منحة إنسباير للطلاب الممولة من مؤسسة ويلكوم ترست التابعة لأكاديمية العلوم الطبية. وقد قُدمت هذه المنحة للأطباء سي. إس روتلاند وف. جيمس وك. برايثويت وك. كوب والأستاذين ن. مونجان وج. إنجلاند لتعزيز البحث والمشاركة العامة. ونشعر بالامتنان تجاه الأستاذ مالكولم كوب لتزويدنا بمخطط كهربية القلب لاستخدامه في شكل 3. ونتقدم بالشكر أيضًا لجمعية لينيان والصندوق الوطني لمحو الأمية لدعم كاثرين بصفتها سفيرة للكتابة العلمية للشباب. ونشكر أيضًا جمعية العلوم البريطانية وجامعة نوتنغهام لمنح كاثرن زمالة الإعلام التابعة لجمعية العلوم البريطانية.
مسرد للمصطلحات
علم الأوبئة (Epidemiology): ↑ هو دراسة توزيع الأمراض ومسبباتها والحالات الصحية الأخرى لدى السكان.
معدل الوقوع (Incidence Rate): ↑ هو معدل حالات الإصابة الجديدة بالمرض في حجم السكان المعروف في غضون فترة زمنية معينة.
الانتشار (Prevalence): ↑ هو نسبة السكان المصابين بالمرض في وقت معين.
عدد التكاثر R0: ↑ هو عدد/معدل التكاثر الأساسي الذي يوضح مدى نقل مرض مُعدٍ للعدوى.
الفحص التشخيصي (Diagnostic Test): ↑ فحص طبي يُستخدم لتشخيص مرض أو حالة صحية.
دقة التشخيص (Diagnostic Accuracy): ↑ هي قدرة الفحص على تمييز الفرق بين الأصحاء والمرضى.
تخطيط كهربية القلب (Electrocardio-Graph): ↑ أسلوب يُستخدم لقياس النشاط الكهربائي في القلب، مما يساعد في فهم ما إذا كان القلب يؤدي وظائفه كما ينبغي.
إقرار تضارب المصالح
يعلن المؤلفون أن البحث قد أُجري في غياب أي علاقات تجارية أو مالية يمكن تفسيرها على أنها تضارب محتمل في المصالح.
المراجع
[1] ↑ Brooks, H., Kanjanasaratool, U., Kureh, Y., and Porter, M. 2021. Disease detectives: using mathematics to forecast the spread of infectious diseases. Front. Young Minds. 9:577741. doi: 10.3389/frym.2020.577741
[2] ↑ Sitch, A. J., Dekkers, O. M., Scholefield, B. R., and Takwoingi, Y. 2021. Introduction to diagnostic test accuracy studies. Eur. J. Endocrinol. 184:E5–9. doi: 10.1530/EJE-20-1239
[3] ↑ Clark, N., Alibhai, A., and Rutland, C. S. 2018. Mending a broken heart—the genetics of heart disease. Front. Young Minds 9:19. doi: 10.3389/frym.2018.00019
[4] ↑ Keane, M., Paul, E., Sturrock, C. J., Rauch, C., and Rutland, C. S. 2017. ''Computed tomography in veterinary medicine: currently published and tomorrow's vision,'' in Computed Tomography - Advanced Applications, ed A. M. Halefoglu (London: IntechOpen). p. 271–89.
[5] ↑ Lendner, J. 2021. What is anesthesia? Front. Young Minds 9:524571. doi: 10.3389/frym.2021.524571
