Résumé
Combien font 2 × 4 ? Cela semble facile, mais as-tu déjà pensé à la façon dont tu résous ce problème ? Dans cet article, tu découvriras deux stratégies différentes que nous utilisons pour résoudre des problèmes d’arithmétique. Tu apprendras également à connaître les différentes zones du cerveau (comme le sillon intrapariétal) qui fonctionnent ensemble lorsque tu utilises ces différentes stratégies. La stratégie et les régions du cerveau que tu utilises changent avec le temps à mesure que tu te familiarises avec l’arithmétique. Cette transition est particulièrement visible dans la façon dont les zones cérébrales fonctionnent et communiquent entre elles : certaines zones deviennent plus actives, tandis que d’autres le deviennent moins. Après avoir lu cet article, tu en sauras plus sur les techniques que nous utilisons pour résoudre les problèmes d’arithmétique et les zones du cerveau nécessaires pour trouver les réponses à ton prochain devoir de mathématiques.
Introduction
Parce que les mathématiques sont l’une des compétences les plus importantes à maîtriser, comprendre comment les problèmes d’arithmétique sont résolus peut avoir un très grand impact sur ton quotidien. Non seulement tu as besoin de mathématiques tous les jours à l’école, mais tu en auras aussi besoin dans ta vie d’adulte. Si tu souhaites devenir programmeur, ingénieur ou scientifique, tu seras confronté aux chiffres au quotidien. Parce que les mathématiques sont importantes dans presque tous les emplois, les personnes peu douées en mathématiques ont parfois du mal à trouver un travail. Certaines d’entre elles pourraient même souffrir de ce qu’on appelle la dyscalculie de développement. Par conséquent, comprendre ce qui se passe dans le cerveau quand on effectue un calcul peut être très utile pour les enfants qui ont des difficultés avec les mathématiques. Comprendre la raison de ces difficultés permet aux enseignants de structurer leurs cours de manière à permettre aux enfants d’apprendre plus facilement. Et bien sûr, être curieux de savoir comment les choses fonctionnent est toujours une raison suffisante pour mener une expérience !
Existe-t-il diverses façons de résoudre un problème arithmétique ?
Pour étudier l’arithmétique, les enfants et les adultes sont généralement invités à résoudre des problèmes d’arithmétique aussi rapidement et précisément que possible. Les problèmes sont généralement présentés sur un écran d’ordinateur, l’un après l’autre (voir Figure 1). Une fois que le participant a répondu, le problème suivant apparaît. Pour étudier les différentes stratégies que nous utilisons en arithmétique, les scientifiques utilisent généralement un mélange de différentes opérations arithmétiques de difficulté variable.

- Figure 1 - Exemple de mise en place d’une étude portant sur la résolution de problèmes arithmétiques.
- Les participants sont confrontés à un problème arithmétique sur un écran d’ordinateur. Une fois la réponse donnée, un nouveau problème apparaît. Pour chaque problème, les chercheurs notent le temps qu’il a fallu pour résoudre le problème (vitesse) et si la réponse était correcte (précision).
En utilisant ces méthodes, les scientifiques ont découvert que les problèmes arithmétiques peuvent être divisés en deux catégories : les petits et les grands problèmes. Les petits problèmes sont résolus très rapidement et les participants font moins d’erreurs lors de la résolution de ces problèmes. Un bon exemple serait «2 × 4». Les grands problèmes sont généralement plus difficiles à résoudre. Les participants mettent plus de temps à résoudre ces problèmes et font également plus d’erreurs. Un bon exemple serait «12 × 3». Les scientifiques sont parfois en désaccord sur la façon dont on peut définir la limite entre les petits et les grands problèmes. La difficulté à résoudre un problème dépend de ton âge et de tes capacités. Cependant, les différences de vitesse et d’erreur entre les petits et les grands problèmes suggèrent que nous utilisons deux stratégies principales pour les résoudre [2].
La première stratégie, à savoir le calcul de la réponse, est souvent utilisée pour de grands problèmes. C’est ce qu’on appelle la stratégie procédurale, car trouver la réponse implique plusieurs étapes - ou plusieurs procédures. Par exemple, pour résoudre «12 × 3», tu peux diviser le problème en deux plus simples comme «10 × 3 = 30» et «2 × 3 = 6». Ensuite, tu peux additionner les résultats pour obtenir la réponse : «36». Mais l’ajout d’étapes supplémentaires a ses inconvénients. Cela prend plus de temps et chaque étape augmente également le risque de faire des erreurs. Cependant, ce n’est pas la stratégie que tu utiliseras toujours pour résoudre ce même problème. Après l’avoir résolu plusieurs fois, la bonne réponse apparaîtra un jour dans ta tête. Cela montre que la façon dont tu résous ce problème a changé.
Tu utilises maintenant la deuxième stratégie : connaître la réponse par cœur - souvent appelée «recherche de faits». En pratiquant le même problème plusieurs fois, tu as stocké sa réponse dans ta mémoire à long terme. Le passage de l’utilisation de stratégies procédurales à l’utilisation de la recherche de faits est une étape importante dans le développement des capacités arithmétiques [3]. Au lieu de calculer la réponse, tu peux maintenant t’en souvenir. De plus, en devenant meilleur pour résoudre des problèmes plus faciles, tu deviens également meilleur pour résoudre des problèmes plus difficiles. Pour mieux comprendre ces changements, nous devons regarder à l’intérieur de notre cerveau pendant qu’il résout les problèmes d’arithmétique. Pour ce faire, les scientifiques utilisent différents outils, tels que l’électroencéphalographie (EEG) et l’imagerie de résonance magnétique fonctionnelle (IRMf, voir Figure 2).

- Figure 2 - Enfants participant à l’une de nos études d’imagerie par résonance magnétique fonctionnelle (IRMf, à gauche) et d’électroencéphalographie (EEG, à droite).
- Ces deux outils permettent aux scientifiques d’étudier le cerveau pendant qu’il fonctionne.
Quelles zones du cerveau sont impliquées dans la résolution des problèmes arithmétiques ?
Essayer de comprendre le fonctionnement du cerveau peut parfois donner l’impression que l’on est en train de résoudre un puzzle compliqué. Tout comme un puzzle qui est composé de différentes pièces, ton cerveau est composé de différentes zones cérébrales (voir Figure 3). Comprendre la fonction de chaque zone cérébrale te donnera une image plus claire de la façon dont elle s’intègre dans le puzzle.
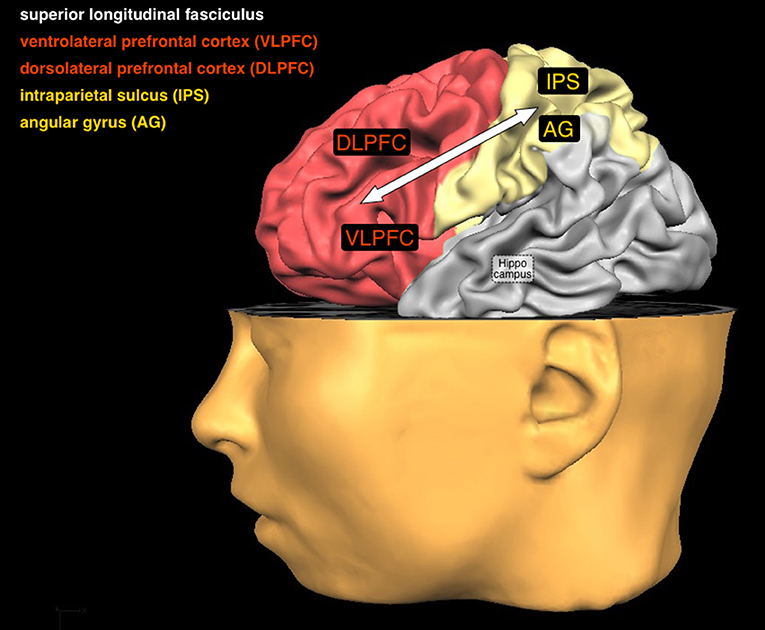
- Figure 3 - Dans cette figure, tu peux voir un certain nombre de zones cérébrales et une connexion qui sont importantes pour l’arithmétique.
- Deux d’entre elles se trouvent dans le cortex frontal (rouge) et deux dans le cortex pariétal (jaune). La façon dont elles fonctionnent ensemble lorsque tu calcules dépend de ton âge et de tes capacités. Une autre zone cérébrale importante, l’hippocampe, se trouve au centre même de ton cerveau et n’est donc pas visible.
La première pièce du puzzle est le sillon intrapariétal. Il est situé dans le cortex pariétal et est chargé de comprendre la signification des nombres [4]. La première étape de la résolution d’un problème arithmétique est de comprendre la grandeur d’un nombre. Par exemple, tu dois savoir que «4 chiens» sont plus que «2 chiens». Tu dois également comprendre l’ordre des nombres (c’est-à-dire que «1» vient avant «2», que «2» vient avant «3», et ainsi de suite). Lors du calcul, tu utilises ta compréhension de la grandeur et de l’ordre pour trouver la bonne réponse.
Les pièces suivantes du puzzle impliquent trois zones cérébrales dans le cortex frontal. Le cortex préfrontal ventrolatéral travaille avec les régions du cortex pariétal pour atténuer les distractions, comme lorsque tu rêvasses à propos de ta prochaine balade à vélo avec tes amis. Le cortex préfrontal dorsolatéral est nécessaire pour manipuler les nombres, comme pour diviser un gros problème en étapes plus faciles. Il s’avère que le gyrus frontal inférieur joue un rôle important parce qu’il ignore les réponses similaires qui se trouvent être incorrectes [5].
Les dernières pièces de notre puzzle sont l’hippocampe et le gyrus angulaire. L’hippocampe est situé au plus profond de ton cerveau. Il joue un rôle important dans le stockage des faits arithmétiques [6]. L’hippocampe est le bouton «enregistrer» de ton cerveau. En matière de mathématiques, il fonctionne avec le cortex frontal pour t’aider à stocker les réponses aux problèmes arithmétiques sous forme de faits arithmétiques dans ta mémoire à long terme. Le gyrus angulaire est alors impliqué dans la recherche de ces faits lorsque tu résous des problèmes arithmétiques.
Comment la résolution des problèmes arithmétiques change-t-elle à mesure que nous vieillissons ?
As-tu déjà tenté d’assembler un puzzle difficile avec des amis ? Si tel est le cas, vous avez probablement travaillé ensemble pour le résoudre. Ton cerveau fonctionne de la même manière. Différentes régions du cerveau travaillent ensemble lors de la résolution d’un problème. La dernière pièce de notre puzzle consiste à comprendre comment ces zones cérébrales fonctionnent ensemble lorsque tu effectues des calculs. Comme tu le sais maintenant, la façon dont tu résous les problèmes arithmétiques change à mesure que tu vieillis. Au lieu d’utiliser principalement des stratégies procédurales pour résoudre des problèmes d’arithmétique, tu commences à utiliser plus souvent la recherche de faits. Mais ce n’est pas la seule chose qui change. Les scientifiques ont découvert qu’au cours de ce processus, la manière dont les différentes zones du cerveau fonctionnent ensemble change également. Par exemple, lorsque tu es jeune, le cortex frontal joue un rôle très important. Il gère ta mémoire de travail et ton attention, car la façon dont tu résous les problèmes arithmétiques implique plusieurs étapes (stratégies procédurales). Lorsque tu vieillis et que tu commences à utiliser la recherche de faits, le rôle de ton cortex frontal change. Lorsque tu regardes le cortex frontal à l’aide de l’IRMf ou de l’EEG, tu peux voir qu’il devient moins actif à mesure que tu vieillis. Il est toujours impliqué dans le processus de recherche de la bonne réponse, mais il n’a pas à travailler aussi dur qu’avant. Peut-être as-tu vécu quelque chose de similaire en coopérant avec tes amis. Au début, l’un de vous devait peut-être garder un œil sur le progrès de chacun et donner des instructions sur la marche à suivre (semblable au cortex frontal). Après avoir résolu avec succès quelques énigmes ensemble, vous êtes en mesure de travailler ensemble sans avoir besoin de quelqu’un chargé de vérifier le progrès de chacun. Le rôle de l’hippocampe change également. Lors de la recherche des faits, il est plus actif chez les jeunes enfants que chez les adultes [7]. En effet, lorsque tu es jeune, l’hippocampe travaille toujours dur pour enregistrer les réponses aux problèmes d’arithmétique dans ta mémoire à long terme. En vieillissant, ton hippocampe doit travailler de moins en moins, car tu rencontres de moins en moins de nouvelles réponses à enregistrer.
Toutes les zones du cerveau travaillent ensemble en communiquant les unes avec les autres. Cette communication se produit sur un vaste réseau de voies (appelées «matière blanche») qui relient toutes les zones du cerveau. Ces réseaux sont similaires à la manière dont les routes relient différentes villes. L’une de ces routes dans le cerveau est appelée le fascicule longitudinal supérieur. Cette route relie le cortex préfrontal au cortex pariétal (où se trouve l’IPS) [8]. Parce que diverses régions du cerveau sont impliquées dans le processus de résolution de problèmes arithmétiques à certains moments de ta vie, les connexions entre ces régions changent également. Les scientifiques essaient toujours de comprendre pleinement comment et pourquoi ces connexions changent avec l’âge. Cela signifie que, même si nous en savons déjà beaucoup sur la façon dont tu résous les problèmes arithmétiques, nous devons faire davantage de recherches pour compléter le puzzle du cerveau calculateur.
Récapitulatif
Même si à première vue cela s’apparente à un processus simple, la résolution d’un problème arithmétique implique de nombreuses étapes. Par ailleurs, plus nous vieillissons, plus nous utilisons des stratégies différentes pour résoudre ces problèmes d’arithmétique. Presque toutes les parties impliquées dans ton cerveau changent. Dans un premier temps, de nombreuses zones du cerveau travaillent ensemble pour résoudre un problème arithmétique. Certaines parties te permettent de rester concentré sur la tâche, d’autres en gardent une trace et mémorisent les résultats de tes calculs. L’hippocampe enregistre le résultat correct dans ta mémoire à long terme. En vieillissant, tu n’as besoin que de quelques zones cérébrales spécialisées pour résoudre le même problème. Ton cerveau fonctionne maintenant très efficacement. La prochaine fois que tu feras tes devoirs de maths, prends une minute pour réfléchir à toutes les différentes zones du cerveau impliquées !
Glossaire
Dyscalculie de développement: ↑ Il s’agit d’une difficulté à apprendre ou à comprendre l’arithmétique. Pour un bon aperçu de l’article de Young Minds; Quand votre cerveau ne peut pas faire 2 + 2 : un cas de dyscalculie de développement [1].
Électroencéphalographie (EEG): ↑ Un outil de neuroscience pour mesurer les signaux électriques produits par le cerveau. Cette méthode peut nous dire avec une grande précision à quel moment les zones cérébrales effectuent une tâche spécifique.
Imagerie de résonance magnétique fonctionnelle (IRMf): ↑ Un outil pour mesurer les différences d’oxygène dans le cerveau. Parce que les zones actives ont besoin de plus d’oxygène lorsque nous effectuons une tâche, nous pouvons définir avec une grande précision les parties qui font le travail.
Zones du cerveau: ↑ Le cerveau peut être divisé en quatre parties principales : le cortex frontal, le cortex pariétal, le cortex temporal et le cortex occipital. Chaque cortex contient des zones cérébrales ayant des fonctions uniques.
Mémoire de travail: ↑ Une fonction cruciale de ton cerveau. Semblable à la mémoire de travail d’un ordinateur, elle stocke des informations dans ton esprit afin de pouvoir les utiliser lorsque tu en as besoin.
Conflit D’intérêts
Les auteurs déclarent que les travaux de recherche ont été menés en l’absence de toute relation commerciale ou financière pouvant être interprétée comme un potentiel conflit d’intérêts.
Remerciements
Nous tenons à remercier de tout cœur ceux qui ont aidé à la traduction des articles de cette collection pour les rendre plus accessibles aux enfants en dehors des pays anglophones, et la Fondation Jacobs pour avoir fourni les fonds nécessaires pour traduire les articles.
Déclaration d’utilisation des outils d’IA
Tout texte alternatif fourni avec les figures de cet article a été généré par Frontiers grâce à l’intelligence artificielle. Des efforts raisonnables ont été déployés pour garantir son exactitude, notamment par une relecture par les auteurs lorsque cela était possible. Si vous constatez des problémes, veuillez nous contacter.
Références
[1] ↑ Bugden, S., and Ansari, D. 2014. When your brain cannot do 2 + 2: a case of developmental dyscalculia. Front. Young Minds 2:8. doi: 10.3389/frym.2014.00008
[2] ↑ Siegler, R. S. 1996. Emerging Minds: The Process of Change in Children’s Thinking. New York, NY: Oxford University Press. doi: 10.5860/choice.34-5984
[3] ↑ De Smedt, B. 2016. “Individual differences in arithmetic fact retrieval,” in Mathematical Cognition and Learning, eds D. B. Berch, D. C. Geary, and K. M. Koepke (San Diego, CA: Academic Press). p. 219–43. doi: 10.1016/B978-0-12-801871-2.00009-5
[4] ↑ Vogel, S. E., Goffin, C., and Ansari, D. 2015. Developmental specialization of the left parietal cortex for the semantic representation of Arabic numerals: an fMR-adaptation study. Dev. Cogn. Neurosci. 12, 61–73. doi: 10.1016/j.dcn.2014.12.001
[5] ↑ De Visscher, A., Vogel, S. E., Reishofer, G., Hassler, E., Koschutnig, K., De Smedt, B., et al. 2018. Interference and problem size effect in multiplication fact solving: individual differences in brain activations and arithmetic performance. Neuroimage 15:718–27. doi: 10.1016/j.neuroimage.2018.01.060
[6] ↑ Qin, S., Cho, S., Chen, T., Rosenberg-Lee, M., Geary, D. C., and Menon, V. 2014. Hippocampal-neocortical functional reorganization underlies children’s cognitive development. Nat. Neurosci. 17:1263–9. doi: 10.1038/nn.3788
[7] ↑ Cho, S., Metcalfe, A. W. S., Young, C. B., Ryali, S., Geary, D. C., and Menon, V. 2012. Hippocampal–prefrontal engagement and dynamic causal interactions in the maturation of children’s fact retrieval. J. Cogn. Neurosci. 24:1849–66. doi: 10.1162/jocn_a_00246
[8] ↑ Matejko, A. A., and Ansari, D. 2015. Drawing connections between white matter and numerical and mathematical cognition: a literature review. Neurosci. Biobehav. Rev. 1:35–52. doi: 10.1016/j.neubiorev.2014.11.006