ملخص
عند انتخاب مندوبين في مجلس النواب الأمريكي (أو الهيئات التشريعية للولاية، أو حتى مجلس إدارة المدرسة)، تجري عملية الانتخاب عن طريق تقسيم الأشخاص إلى دوائر انتخابية، وتنتخب كل دائرة مندوبًا واحدًا يمثلها. قد تؤثر الدوائر الانتخابية التي نرسمها كأشكال على الخرائط على نتيجة الانتخابات. ونتيجةً لذلك، تحظى عملية إنشاء أو تغيير الدوائر الانتخابية، والأشكال التي نرسمها خلال إنشاء تلك الدوائر بأهمية كبيرة. وبعد كل عملية تعداد للسكان، يجب على كل ولاية إعداد خريطة جديدة للدوائر الانتخابية. وعند إجراء عملية انتخابية غير عادلة، قد يقدم ذلك ميزة غير عادلة لأحد الأحزاب السياسية. وهذا ما يُعرف باسم التلاعب في الدوائر الانتخابية (التزوير الانتخابي). فمن خلال النظر إلى أشكال الدوائر وفحص الكتل السكانية، يمكننا البدء في التمييز بين خرائط الدوائر النزيهة وغير النزيهة.
هل تعد الانتخابات نزيهة؟
كثيرًا ما تُستخدم الانتخابات لاتخاذ مجموعة متنوعة من القرارات؛ على سبيل المثال، ربما تكون قد أدليت بصوتك بالفعل على نشاط أو مكافأة في الفصل، أو داخل إطار العائلة. وتعد هذه سمة مشتركة بين الحكومات؛ لأنها تسمح للناخبين المصوتين بالتعبير عن آرائهم وجمع تلك الآراء لاتخاذ قرار ما. وعند الاختيار من بين أكثر من خيارين، أو عند تصويت العديد من الأشخاص بطرق مختلفة أو في أماكن متفرقة، تصبح الانتخابات معقدة، وقد تبدو العملية أو النتائج غير نزيهة. ما معنى أن تكون الانتخابات نزيهة أو غير نزيهة؟ اتضح أن هناك الكثير من الجوانب التي يمكننا دراستها في هذا الجانب، لكننا سنركز على جانب واحد فقط وهو ما يدرسه علماء الرياضيات مؤخرًا: عند تقسيم الأشخاص إلى مجموعات للتصويت، كيف تؤثر الأشكال التي نرسمها على الانتخابات؟
في الولايات المتحدة، تنتخب كل ولاية المسؤولين العاملين في جزء من الحكومة الفيدرالية يعرف بمجلس النواب. وعلى نحو أكثر تحديدًا، تُقسم الولايات نفسها إلى دوائر انتخابية، وتنتخب كل منها شخصًا واحدًا في مجلس النواب. على سبيل المثال، يوجد في فلوريدا 27 دائرة انتخابية، وفي كولورادو 7 دوائر انتخابية. وبما أنه يحق للجميع التصويت، فلماذا تعتبر الدوائر الانتخابية مهمة؟ إذا صوّت كل شخص في ولاية ما بنفس الطريقة، فلن تحظى الانتخابات بأهمية على الإطلاق، لكن قلما ما يحدث ذلك. فإذا كان بعض سكان الولاية يفضلون الحزب ”أ“ والبقية يفضلون الحزب ”ب“، فمن المنطقي أن يكون بعض ممثلي الولاية من الحزب ”أ“ والبعض الآخر من الحزب ”ب“؛ وذلك لتمثيل خيارات التصويت للولاية بأكملها على نحو أكثر دقة. وإذا كانت هناك دائرة انتخابية تضم ناخبين للحزب ”أ“ أكثر من ناخبي الحزب ”ب“، فسوف ينتخبون ممثلًا من الحزب ”أ“، والعكس صحيح.
إنشاء الدوائر الانتخابية
كل 10 سنوات، يُجرى التعداد السكاني في الولايات المتحدة، وهو يحصر كل شخص يعيش في البلد ويسجل مكان إقامته [1]. وبناءً على أرقام التعداد، يتم إبلاغ كل ولاية بعدد النواب الذين يمكن انتخابهم. وعليه، ترسم الولايات خرائط جديدة للدوائر الانتخابية بناءً على عدد النواب المسموح به. لكن السؤال هنا: كيف تُقسم الولايات الأشخاص للتصويت؟ وأي الأشكال تعد نزيهة؟
في البداية، دعونا نفكر في ثلاثة مخططات مختلفة ممكنة. أولًا، هل يمكننا فرض شبكة على كل ولاية، مثل ورق الرسم البياني؟ للولايات حدود غير منتظمة وأجزاء وعرة، ولكن ربما يكون استخدام مربعات متساوية بداية جيدة لهذا الأمر. وقد تشمل الطريقة الثانية استخدام التقسيمات الموجودة بالفعل في الولايات - هل يمكن أن تمثل كل بلدة (أو أبرشيّة) دائرة انتخابية؟ بما أن هذه الحدود مرسومة وقد تم الاتفاق عليها بالفعل، فيبدو أن هذه طريقة منطقية للبدء بها. ثالثًا، ربما يمكننا محاولة خلط الأشخاص. فهل يمكن تخصيص كل ناخب لدائرة ما بشكل عشوائي، بحيث يتم توزيع جميع الدوائر الانتخابية في جميع أنحاء الولاية؟ لاختيار الطريقة الأمثل من بين جميع الطرق الممكنة، نحتاج أولاً إلى فهم القواعد التي يجب أن تتبعها الدوائر الانتخابية.
قواعد وضع خرائط الدوائر الانتخابية
القاعدة الأولى التي يجب على الدوائر الانتخابية اتباعها هي أنه يجب أن يكون في كل دائرة انتخابية نفس العدد من الأشخاص. وتعد هذه القاعدة الوحيدة الموجودة في دستور الولايات المتحدة الخاصة بإعادة تقسيم الدوائر. وتعد بيانات التعداد السكاني ركيزة أساسية في وضع خرائط الدوائر الانتخابية. ونتيجةً لذلك، قد تتخذ الدوائر المرسومة على الخريطة أحجامًا مختلفة للغاية في مناطق مختلفة للغاية، ولكن يُسمح بذلك طالما يعيش نفس العدد من الأشخاص في كل منطقة.
ويعني ذلك أن فكرتنا الأولى قد لا تنجح، لأن مربع الشبكة الذي توجد به أي مدينة يحتوي على عدد سكان أكبر بكثير مقارنة بمربع الشبكة الذي يحتوي على مزرعة. ويعني ذلك أيضًا أنه إن لم نكن محظوظين للغاية وكان لكل بلد نفس العدد من السكان، فإن فكرتنا الثانية لن تنجح أيضًا. لكننا لم نستبعد الاقتراح الثالث. هل يمكننا خلط الأشخاص والتأكد من تخصيص نفس العدد من الأشخاص لكل دائرة انتخابية؟
للأسف، الأمر ليس بهذه السهولة لأن هناك المزيد من القواعد التي وضعتها الولايات. كما توجد بعض الاختلافات القائمة بين الولايات والتي يجب أخذها في الاعتبار عند ترسيم الدوائر، لكن الولايات تتفق على أشكال الدوائر المسموح بها: إذ يجب أن تكون كل منطقة متجاورة ومتكتلة [1]. تمثل المناطق المتجاورة القاعدة السهلة: فهي تعني أنه يجب أن تكون الدائرة كلها في منطقة واحدة. لكن ذلك سيجعلنا نستبعد خطة التوزيع العشوائي للجماهير على الدائرة! وإذا قمنا بتوزيع الأشخاص عشوائيًا على الدوائر الانتخابية، فستكون هناك فجوات وقطع متناثرة، ولن تكون الدوائر متجاورة.
أما التكتل فهو القاعدة المثيرة للاهتمام. تمهل للحظة وتصور صنع شيئًا متكتلًا. ربما تخيلت طوي قطعة من الورق أو الضغط على كرة من الطين. على الرغم من أن كلمة ”تكتل“ وُضعت في القوانين على أساس أن الجميع يعرف معناها، فإنها في الحقيقة ليست واضحة تمامًا. وعندما حاول السياسيون والمحامون توضيح المصطلح، توصلوا إلى أكثر من 30 طريقة مختلفة لقياس ”التكتل“ أو وصفه [2]. وبهذا يتبقى الآن سؤال حول الأشكال التي تتطلب طرقًا مبتكرة لفهمها؛ وهذا هو السؤال الشيق الذي جذب علماء الرياضيات.
التلاعب في الدوائر الانتخابية
عندما يكون للأحزاب السياسية رأي في ترسيم خرائط الدوائر الانتخابية، فغالبًا ما تحاول ترسيمها بحيث تتمكن من الفوز بأكبر عدد ممكن من الدوائر الانتخابية. ويسمى ترسيم خرائط الدوائر الانتخابية بطريقة قد تؤثر على من يتم انتخابه بالتلاعب في الدوائر الانتخابية. وعندما يرسم الأشخاص الدوائر الانتخابية للتأثير على نتائج الانتخابات، قد تصبح أشكال الدوائر غريبة. ومن هنا جاء اسم ”التلاعب في الدوائر الانتخابية“ (الجيرماندرية). ففي مطلع القرن التاسع عشر، كان هناك مرشح يدعى ”إلبريدج جيري“ (Elbridge Gerry) سيفوز في انتخابات دائرة أنشئت بطريقة غير نزيهة، وكانت هذه الدائرة غريبة المظهر وذات حواف غير منتظمة وملتفة حول خليج ماساتشوستس (الشكل 1). ومن هنا أطلق رسام كاريكاتير تحريري اسم سمندر جيري (Gerry’s Salamander) على هذه الظاهرة، وظل الاسم مرتبطًا به [1].
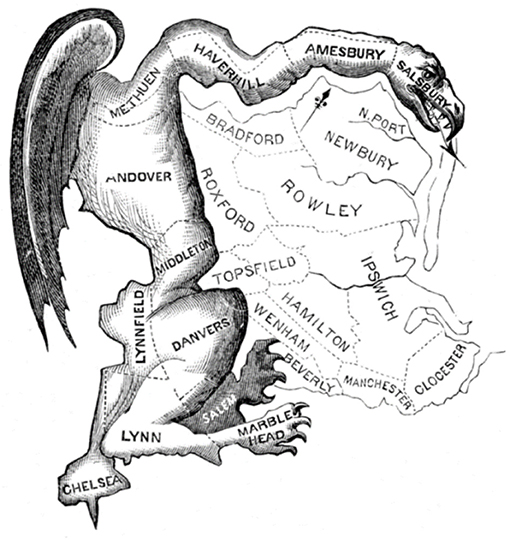
- شكل 1 - أضاف هذا الرسم الكاريكاتيري السياسي، الذي رسمه إلكانه تيسدال، ونُشر في الجريدة الرسمية لبوسطن (Boston Gazette) عام 1812، مخالب وأجنحة وأسنان إلى الدائرة ذات الشكل الغريب التي تلتف حول الحدود الغربية والشمالية للمنطقة الانتخابية في ولاية ماساتشوستس.
- وأطلق عليها تيسدال اسم ”سمندر جيري“ (Gerry’s Salamander) على اسم المرشح السياسي Elbridge Gerry، وتطورت إلى كلمة ”gerrymandering“ (التلاعب في الدوائر الانتخابية)، التي تصف ترسيم الدوائر الانتخابية لتحقيق مكاسب سياسية (بدلًا من النزاهة).
ومنذ ذلك الحين، حاولت الأحزاب السياسية ترسيم الدوائر الانتخابية التي تخدم مصلحة مرشحيها، ويظل النقاش محتدمًا بشأن مدى نزاهة الدوائر الانتخابية من عدمها. تم تناول موضوع التلاعب في الدوائر الانتخابية في قانون حقوق التصويت لعام 1965، ولا يزال المشرعون والمحاكم ينظرون فيه اليوم، وأصدرت المحكمة العليا حكمًا في قضية تتعلق بالتلاعب في الدوائر الانتخابية مؤخرًا في عام 2019.
تحديد الدوائر غريبة الشكل
عند ترسيم الدوائر الانتخابية مع وضع الأهداف الانتخابية في الاعتبار، تميل الأشكال إلى أن تصبح غريبة. وتتمثل طريقة اكتشاف هذا الغرابة في العودة إلى فكرة التكتل. فقد تكون كرة الورق المطوية من وقت سابق متكتلة، لكنها ثلاثية الأبعاد. أما دوائرنا الانتخابية (على الخريطة على الأقل) فهي ثنائية الأبعاد. ويمكن تمثيل الشكل الأقرب للكرة الورقية في صورة بُعدين على شكل الدائرة، لذا فإن إحدى الطرق لبدء التفكير في مدى تكتل المنطقة هي التفكير في طرق تقيس مدى قرب شكل الدائرة الانتخابية من الشكل الهندسي للدائرة.
من الأشياء التي تجعل الدائرة فريدة من نوعها هي أنها الشكل الهندسي الذي يحوي أكبر مساحة في محيط معين؛ فمثلًا إذا كان لديك قطعة من الخيط وترغب في إحاطة أكبر قدر ممكن من الأشياء داخل حدودها، فيمكنك صنع دائرة لتحقيق ذلك. ويمكن التعبير عن مساحة الدائرة المسماة A على النحو التالي: A = πr2، حيث يمثل r نصف القطر. ويمكن التعبير عن محيط الدائرة P على النحو التالي P = 2πr. وإذا أردنا التفكير في العلاقة بين المساحة والمحيط، فيمكننا تكوين نسبة: ، وفكر في الأمر باعتباره ”الدرجة“ التي يحصل عليها هذا الشكل. لكن ظهور نصف القطر (r) في النتيجة يعني أن الدوائر ذات الأحجام المختلفة سيكون لها درجات مختلفة، وهذا ليس دقيقًا لأن الدائرة الأكبر ليست أقل تكتلًا من الدائرة الأصغر. ولمنع حدوث ذلك (أي لإلغاء جميع الوحدات)، يمكننا تربيع المحيط بحيث يكون هناك نصف قطر (r) آخر في المقام، حتى يتم إلغاء هذه القيمة بالكامل. جرب . الآن، ستحصل كل دائرة على الدرجة نفسها. ولكن نظرًا لأن الدوائر هي الشكل الأفضل والأكثر تكتلًا، فقد أراد الأشخاص أن يحصلوا على درجة 1. وسيحدث ذلك إذا أضفنا 4π إلى أعلى درجاتنا، بحيث يتم إلغاء 4π ”المتبقية“: . وتُعرف هذه الدرجة بدرجة اختبار Polsby-Popper [2]. تسجل الدائرة درجة 1، بينما يسجل المربع (طول ضلعه s) درجة ، ويسجل المستطيل الطويل الضيق (على سبيل المثال، وحدة واحدة عرض في 100 وحدة طول) درجة (الشكل 2).
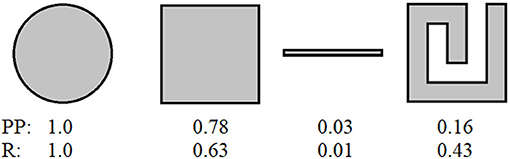
- شكل 2 - درجات اختبار Polsby-Popper وReock لدائرة ومربع ومستطيل طويل ضيق ومربع به قطع ”حلزوني“.
- قد ترى أن درجة Polsby-Popper تدلل على أن الشكل الحلزوني المربع يشبه إلى حد كبير المستطيل الضيق الطويل (يتضمن محيطًا كبيرًا بالنسبة لمساحته)، لكن درجة Reock للمربع الحلزوني تشبه إلى حد بعيد المربع (سيكون لهما دوائر متشابهة تناسبهما). ويمكننا، بدلالة درجات أي من الاختبارين، أن نقول إن كلًا من المستطيل الضيق الطويل والمربع الحلزوني أقل تكتلًا من المربع، لكنهما يختلفان في مدى سوء كل منهما، ومن حيث الأشكال الأكثر تشابهًا مع بعضهما البعض.
وهناك طريقة أخرى محتملة لقياس مدى تشابه شكل هندسي معين مع الدائرة؛ وهي أخذ شكل الدائرة الانتخابية والعثور على أصغر دائرة تتلاءم معها. تخيل البدء بدائرة كبيرة وتقليصها حتى يلامس الشكل الداخلي الدائرة في أماكن كافية بحيث لا توجد مساحة كبيرة للحركة. إذا كان الشكل الداخلي عبارة عن دائرة أيضًا، فستتطابق الأشكال في كل مكان، ولكن إذا لم يكن كذلك، فستكون هناك فجوات بين الشكل الداخلي والدائرة. وكلما كان شكل الدائرة الانتخابية أقل شبهًا بالدائرة، زادت الفجوات الموجودة. ويمكننا بناء نسبة أخرى، ، حيث تمثل A مساحة الدائرة الانتخابية وتمثل C مساحة شكل الدائرة، والتي تسمى درجة Reock [3] للتكتل. وباستخدام هذه الطريقة، سيحصل شكل الدائرة على درجة 1، والمربع على ، ومستطيلنا الضيق الطويل سيسجل درجة .
قد ترى أن الدرجات التي تم الحصول عليها باستخدام هاتين الطريقتين تقل بالترتيب نفسه للأشكال الثلاثة، وهو ما يتوافق مع تخميننا المنطقي، لكنها لا تنقص بالمقدار نفسه في كل طريقة، لأنها تقيس أشياء مختلفة. لكن السؤال هنا: أي مقياس للتكتل يعد الأفضل؟ حسنًا، يعتمد الأمر على عدة محاور، وهي إجابة محبطة. فكر في شكل آخر: مربع به شكل حلزوني مقطوع منه. يحصل هذا الشكل على درجة في اختبار Polsby-Popper تساوي ، ودرجة في اختبار Reock. هل هذا شكل أفضل أم أسوأ لدائرة انتخابية مقارنة بالدوائر الأخرى التي درسناها؟ ما نسبة نجاح المتلاعب الأصلي في الدوائر الانتخابية في الشكل 1 في ظل هذه الدرجات؟
ترسيم الدوائر ليس سهلًا!
قد يبدو تحديد الشكل الأكثر نزاهة للدوائر الانتخابية أمرًا معقدًا بالفعل؛ ولكنه يصبح أكثر تعقيدًا بمرور الوقت! ماذا يحدث عندما تكون الدائرة الانتخابية على ضفاف مياه؟ سيكون جزء من حدودها الخط الساحلي، وهو وعر بطبيعته [4]. عندما تقوم بتكبير الخط الساحلي على خريطتك، سترى المزيد من النتوءات على امتداده (التفاصيل التي أخفاها انخفاض الجودة). تجعل هذه النتوءات قياس الخط الساحلي، وبالتالي محيط الدائرة، أطول، بنسبة كبيرة على الأرجح. فالدائرة الانتخابية هي نفسها، لكن القياسات تختلف بتغيير النظر إلى الخرائط المختلفة. وبالتالي، تختلف الدرجات التي حسبناها. كما نحتاج إلى التفكير مليًا فيما نريد تضمينه عند التفكير في مساحة الدائرة الانتخابية. على سبيل المثال، إذا كانت هناك بحيرة داخل دائرة انتخابية ما، فهل نحسبها كجزء من المساحة؟ وإذا لم نحسب مساحة البحيرة، فهل يتعين علينا حساب الخط الساحلي كجزء من المحيط؟ ولهذه المناقشات أكثر من إجابة واحدة معقولة. تقلل أداة قياس الخرائط المتسقة من هذه المشكلات، ولكن من الصعب تحديد الطريقة الصحيحة.
الانتخابات النزيهة تحتاج إلى خرائط دوائر انتخابية عادلة
تعد الانتخابات جزءًا مهمًا من طريقة اختيار قادتنا، لذا من المهم فهمها ومحاولة إبقائها نزيهة. وتعد أحد الأشياء التي تسلل إليها الظلم في نظامنا هي كيفية تقسيم الأشخاص إلى دوائر انتخابية لاختيار النواب (على مقاعد مجلس نواب الولايات المتحدة)، أو في انتخابات المستويات الأدنى، مثل مجلس إدارة المدرسة أو مجلس المدينة. وعندما يحاول الأشخاص التلاعب في تلك الدوائر الانتخابية، يظهر ذلك التلاعب في أشكالها.
إن درجات اختبار Polsby-Popper وReock ليست سوى طريقتين من عدة طرق ابتكرها الأشخاص لقياس التكتل في الدوائر الانتخابية. وتحديد المقاييس الأكثر نزاهة ليس مجرد سؤال في الرياضيات - بل إنه أمر علينا أن نقرره كمجتمع. ومع ذلك، قد تساعدنا الرياضيات في توضيح الأسئلة. ويوضح علماء الرياضيات أيضًا أن نوعًا واحدًا من الدرجات قد يُخطئ في رصد أنواع مختلفة من حالات فشل التكتل، ولكن إذا نظرنا إلى عدة مقاييس مختلفة معًا، فمن المحتمل أن نتمكن من توضيح التلاعب في الدوائر الانتخابية بنجاح. وتعد خرائط الدوائر الانتخابية النزيهة جزءًا مهمًا من الانتخابات النزيهة، ومن خلال النظر إلى التكتل واستخدام العديد من الأدوات الأخرى، تساعدنا الرياضيات على تحسين اكتشاف عدم النزاهة.
مسرد للمصطلحات
دائرة انتخابية (District): ↑ الدائرة الانتخابية هي منطقة جغرافية تشارك معًا في الانتخابات. فمثلًا، في انتخابات مجلس النواب، تنتخب كل دائرة ممثلًا واحدًا في مجلس النواب.
الدوائر المتجاورة (Contiguous): ↑ تكون أي دائرة انتخابية (أو أي شكل هندسي آخر) متجاورة إذا كانت كلها في قطعة واحدة. ويمكنك التنقل بين أي مكانين في الدائرة دون مغادرتها.
التكتل (Compact): ↑ تكون أي دائرة انتخابية (أو أي شكل آخر) متكتلة إذا اقتربت أجزائها من بعضها البعض. وهناك جدل قائم حول كيفية تعريف هذا المصطلح، لكننا سنقول إن التكتل يشبه حلقة دائرية.
التلاعب في الدوائر الانتخابية (Gerrymandering): ↑ التلاعب في الدوائر الانتخابية هو ترسيم خرائط الدوائر الانتخابية بهدف إعطاء مجموعة سياسية واحدة الأفضلية في الانتخابات، بدلًا من ترسيم خرائط الدوائر الانتخابية لتعكس آراء الناخبين بإنصاف.
درجة اختبار (Polsby-Popper): ↑ تجمع هذه الدرجة بين محيط الدائرة ومساحتها في المعادلة . ستحصل الدائرة على درجة 1، بينما تحصل الأشكال الأقل تكتلًا على درجات بين 0 و1.
درجة اختبار (Reock): ↑ تقارن هذه الدرجة مساحة الدائرة الانتخابية بمساحة الدائرة الأصغر التي تحتوي عليها وفقًا للمعادلة. وتحصل الدائرة في هذا الاختبار على درجة 1.
إقرار تضارب المصالح
يعلن المؤلفون أن البحث قد أُجري في غياب أي علاقات تجارية أو مالية يمكن تفسيرها على أنها تضارب محتمل في المصالح.
المراجع
[1] ↑ ACLU. 2010. Everything You Wanted to Know About Redistricting But Were Afraid to Ask. Voting Rights Project. Available online at: www.aclu.org/voting-rights
[2] ↑ Lunday, B. J. 2014. A metric to identify gerrymandering. Int J Soc Syst Sci. 6:285–304. doi: 10.1504/ijsss.2014.065207
[3] ↑ Young, H. P. 1988. Measuring the compactness of legislative districts. Legis Stud Q. 13:105–15.
[4] ↑ Mandelbrot, B. 1967. How Long is the coast of Britain? Statistical self-similarity and fractional dimension. Science. 156:636–8.
