Abstract
Most cars use gasoline as a fuel. But cars can run on other fuels, such as natural gas (NG), the same gas that is used for cooking and for heating our homes. NG is cheaper and possibly better for the environment than gasoline. However, gasoline is much more dense than NG since gasoline is a liquid and NG is a gas. So, to run a car on NG, we need to increase its density so that we can fit enough NG in the fuel tank to drive a similar distance as with a tank of gasoline. Researchers around the world are working on synthesizing materials that act as sponges that adsorb NG. By putting these sponge-like materials inside of the fuel tank, we can increase the density of NG to efficiently store it onboard the vehicle. In our study, we show that how computers can be used to search for the most promising sponge-like materials to store NG.
Natural gas (NG) is an attractive fuel for vehicles as an alternative to gasoline. The United States has an abundant supply of NG, much of it trapped in deep, underground rock formations. The recent increase in the use of hydraulic fracturing (known as “fracking”) and horizontal drilling has made it possible for us to extract more of this NG. This abundant supply, which is expected to last far into the future, makes NG a relatively cheap alternative to gasoline. There are many discussions about the impact of fracking on the environment, but, on the other hand, NG as a fuel may be less harmful to the environment than gasoline. For example, burning NG releases 25% less carbon dioxide than burning gasoline. Carbon dioxide is the greenhouse gas primarily responsible for global warming. NG is mostly methane, which itself is a potent greenhouse gas. So, to take advantage of the environmental benefits of NG, we must be careful to avoid additional emissions of methane as a result of an increase in the production, transportation, and use of NG as a fuel for vehicles.
If NG has economic and possibly environmental advantages over gasoline, why are most cars still running on gasoline? The problem is that NG suffers from a low energy density. The Energy density is an important quantity, as it tells us how much energy we can obtain from a given volume of fuel. The more energy we have in our fuel tank, the longer distance we can drive before we need to refill our tank. Let us now compare the energy densities of NG and gasoline at room temperature and atmospheric (normal) pressure. The energy density of gasoline is 950 times higher than the energy density of NG. The reason is that molecules are very far apart in a gas compared to in a liquid, leading to less molecules per volume. What this means in practice is illustrated in Figure 1; to drive the same distance with NG, we need to take with us 950 times the volume of NG as we would if we were carrying gasoline. A typical gasoline tank can contain 50 L; imagine what a car would look like with a tank 950 times bigger!
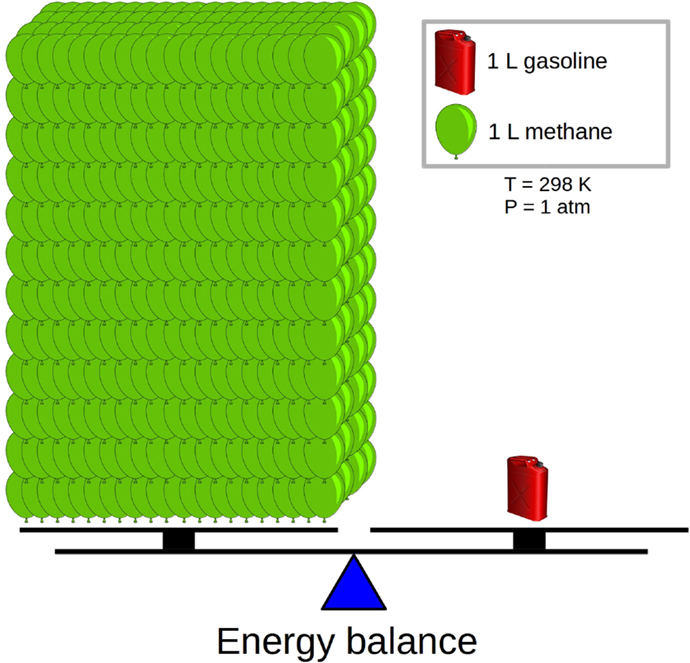
- Figure 1 - Energy balance - both sides of the balance allow us to drive the same distance (left: natural gas, right: gasoline).
- At room temperature (298 K) and atmospheric (normal) pressure (1 atm), burning 1 L of gasoline yields 950 times the energy of burning 1 L of natural gas, which is mostly methane.
Thus, to use NG as a vehicular fuel without such impractically large fuel tanks, we need to put more methane molecules into the fuel tank. Two strategies are used today to increase the energy density of a tank filled with NG. One strategy is to compress NG; at a higher pressure, there are more gas molecules in the same volume. The other strategy is to cool NG to such a low temperature that it becomes a liquid, a process called liquefaction. Since molecules in a liquid are much closer together than in a gas, this increases the energy density.
Increasing the Density of Natural Gas
For Liquefied natural gas (LNG), the NG is cooled to a very low temperature, around –162°C (–260°F), so that it condenses into a much denser liquid. LNG has some problems that prevent it from being used for passenger vehicles. The process used to liquefy NG takes a lot of energy. Big, expensive, specialized fuel tanks are required to store LNG at such low temperatures. Unfortunately, the heat insulation on these tanks is not perfect. Therefore, to keep LNG cool, some NG needs to be vented into the atmosphere. Venting not only keeps the LNG cool but also wastes fuel and more importantly releases methane into the atmosphere, adding to global warming.
For Compressed natural gas (CNG), the NG is compressed at room temperature to around 200 times atmospheric pressure. The problem with CNG is that the compression equipment needed to achieve such a high pressure is expensive. Furthermore, the fuel tanks in the vehicles using CNG must have thick walls and a spherical or cylindrical shape to withstand such a high pressure. This makes for a heavy, expensive tank, which only fits in the trunk of the vehicle, leaving no space for luggage. The tank that is used for gasoline, however, can be any shape and therefore is designed and placed to more efficiently use space in the car.
In Figure 2, we compare the energy density of LNG and CNG to the energy density of gasoline. The energy density of a balloon filled with NG at room temperature and atmospheric pressure is also shown, demonstrating that LNG and CNG have a much higher energy density than a balloon of NG. While the density of CNG or LNG is not as high as gasoline, it is high enough that we can still drive quite a long distance with a fuel tank containing CNG or LNG.
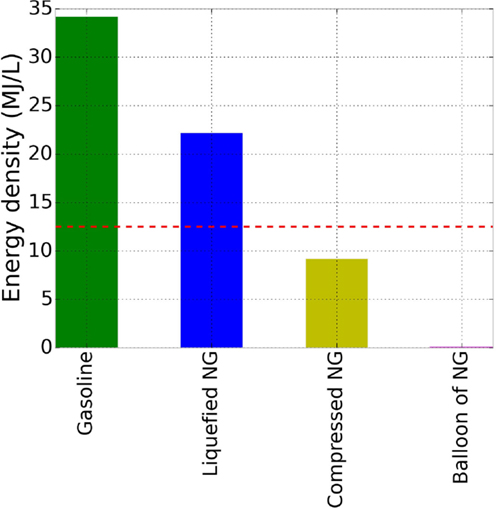
- Figure 2 - Energy density of fuels.
- We compare the energy density of gasoline to natural gas (NG) at different conditions [1]. Gasoline has the highest energy density, almost 35 MJ/L. The most dense form of natural gas is liquefied natural gas, and then compressed natural gas. On the far right, the energy density of a balloon of natural gas at room temperature and atmospheric pressure is so small (0.036 MJ/L) that we can barely see the purple bar! The red, dashed line is the ARPA-E energy density goal for storing methane in sponge-like nanoporous materials (12.5 MJ/L).
Researchers are looking for alternative strategies to increase the energy density of a tank filled with NG because of these practical difficulties with LNG and CNG. One idea, and the focus of this article, is to make a material that acts as a sponge for methane. We then put this material inside the fuel tank and hope that it will attract so many methane molecules that we can achieve an energy density as high as CNG, but using a lower pressure. Because the storage pressure of methane stored in sponge-like materials can be lower than the pressure needed to store CNG, the fuel tanks can be thinner, cheaper, and made in any shape to more easily fit in the vehicle. In addition, the compressors to achieve this lower pressure are cheaper than those for CNG, so we may be able to refill our tanks at home, using the same gas we are already using for cooking and heating.
The materials that are the most promising sponges are called Nanoporous materials. Figure 3 shows an example of such a material. A nanoporous material is a structure with pores or cages with a diameter of around a nanometer. A human hair is about 80,000 nm thick; a nano-sized pore is so much smaller that only molecules can fit inside. A methane molecule has a diameter of 0.3 nm, so methane molecules can fit comfortably in the pores. A methane molecule is attracted to the walls of the porous material. As a result, methane molecules stick to the interior surface of the solid material. This process of molecules sticking to the interior surface of the material is called Adsorption. To get an idea of how many methane molecules a nanoporous material can adsorb, consider if we could unravel and flatten the surface of the walls of these pores: a single gram of these nanoporous materials has the surface area of more than a football field!

- Figure 3 - Example of a nanoporous material, Cu-BTC.
- The top figures show a nanoporous material, a Metal-organic framework (MOF) called Cu-BTC [2]. The color is blue due to the copper content in Cu-BTC. By putting this material inside the fuel tank, we can achieve a higher energy density because this material behaves as a sponge for natural gas molecules. The bottom figure shows the molecular structure of Cu-BTC. The spheres represent atoms, and the sticks show how the atoms are bonded to each other; different colors are used for different elements (orange: copper, red: oxygen, gray: carbon, white: hydrogen). The walls of the hole-like pores in this material form an interior surface to which gas molecules stick, endowing it with its sponge-like behavior. The diameter of these pores is ~0.7 nm.
A US government agency called Advanced Research Projects Agency-Energy (ARPA-E), has started a multi-million dollar program to pay for research aimed to find a material for NG storage for use in vehicles. In this program, ARPA-E set the goal that a nanoporous material should achieve an energy density of 12.5 MJ/L (see red, dashed line in Figure 2). This energy density goal is 340 times that of NG at room temperature and atmospheric pressure. A material with these properties would allow the use of lighter, thinner storage tanks and cheaper compression equipment. Researchers all over the world are trying to discover new materials that meet the methane storage goal set by ARPA-E.
Finding the Best Nanoporous Materials
An exciting aspect of advanced nanoporous materials is that chemists can design them at the molecular level and thereby tune their pores to improve their performance. Chemists can synthesize millions of different possible materials by mixing together different molecular building blocks (see Figure 4).
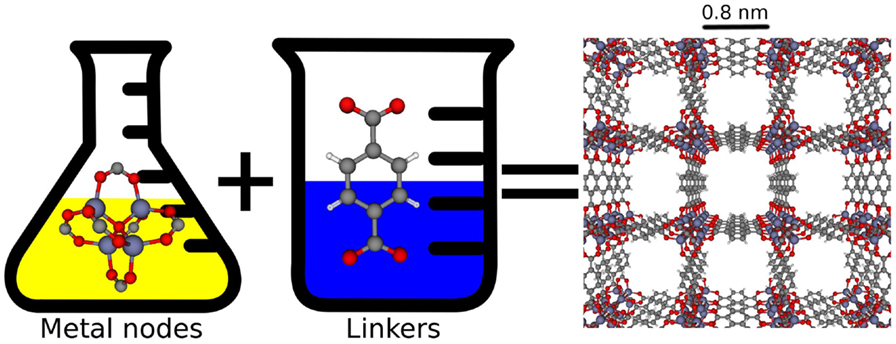
- Figure 4 - Chemical tunability of advanced nanoporous materials.
- On the right is the structure of a metal-organic framework (MOF) called IRMOF-1 [3]. IRMOF-1 is made in the laboratory by combining two different molecular building blocks: metal nodes and organic linkers. These linkers and nodes assemble themselves in solution to form the repeating nanoporous crystal structure of IRMOF-1. By changing the linkers and metal nodes, millions of different metal-organic frameworks can be created (Image concept by Katie Deeg).
In a laboratory, it takes a few weeks to synthesize and test a new material. It would take too long to synthesize millions of different materials and test all of them to see which adsorbs the most NG. This gives us important research questions: out of the millions of possibilities, how can researchers know which combination of molecular building blocks will yield a material that meets the ARPA-E’s storage capacity goal? How do we even know that this goal is possible to reach? There are surely limits to how much NG a material can possibly store.
Making and Testing Materials on Computers
Researchers have also been working on a method to make models of materials on a computer. By snapping together different molecular building blocks, much like they were Lego blocks or K’NEX, researchers can make computer models of these materials. As making model materials on a computer goes much faster than making real materials in the laboratory, many model materials can be made.
Once we make a material on a computer, we can run Computer simulations of methane adsorbing into the pores of the material. These computer simulations resemble a flight simulator for molecules; the algorithm inserts, deletes, and moves around methane molecules inside the pores of the material to explore the most favorable configurations. With molecular simulations, we can predict how many methane molecules a given material will adsorb on the basis of the computer-generated structures.
Researchers have constructed over 650,000 different nanoporous materials on computers so far. They have done this by choosing different molecular building blocks and combining them according to rules based on what is known from the laboratory about how to synthesize these materials. Using a molecular simulation computer code that we wrote [4], we simulated methane adsorption and thus predicted how much methane each of these 650,000 nanoporous materials adsorbs.
Out of our database of over 650,000 materials, the structure that we predicted to achieve the highest methane energy density is shown in Figure 5. Our simulations predict that this top material can achieve a methane energy density of 7.8 MJ/L. We hope that this prediction will motivate the synthesis and testing of this computer-generated [4] structure. Still, this structure achieves only 62% of the ARPA-E storage goal of 12.5 MJ/L. Since the best material in our database is quite far from meeting the ARPA-E storage goal, it seems to be very unlikely that the ARPA-E storage goal can be reached.
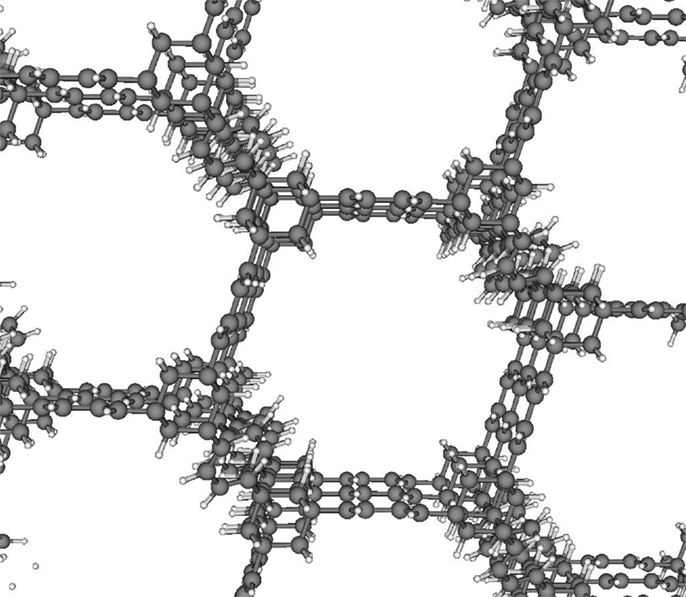
- Figure 5 - Top structure.
- The structure that achieves the highest predicted energy density of methane – 7.8 MJ/L – is shown. The gray spheres are carbon atoms; the white spheres are hydrogen atoms. This is a computer-generated structure that has not been synthesized [5].
The record holders for the highest methane energy density achieved in the laboratory so far are Cu-BTC (Figure 3) and IRMOF-1 (Figure 4), at 7.4 MJ/L [6]. Compared to the top material in our database, achieving an energy density of 7.8 MJ/L, our findings further suggest that there is not much room for improvement upon current materials.
Conclusion
Our work illustrates how we can build computer models of materials and use computer simulations of methane adsorbing into the pores to rapidly and cost-effectively identify the most promising nanoporous materials to store NG. By evaluating such a large number of materials (650,000), which is impractical in the laboratory, we were able to quickly come to the conclusion that the ARPA-E storage goal is unlikely to be met.
Can we now conclude that it is impossible to find a material that meets the ARPA-E goal? First of all, it is important to realize that we can only make computer models of materials that we currently understand from laboratory experiments. However, in the future, chemists could invent completely new classes of materials that are able to reach the storage goal.
Even though we did not find a nanoporous material that meets the ARPA-E methane storage goal, it is not a waste of time to study NG storage with nanoporous materials. Instead, the results suggest that we should think about using the current best nanoporous materials. A material that can achieve an energy density of 8 MJ/L is still a big improvement over using an empty tank at the same pressure, which has an energy density of only 2.5 MJ/L. Packing the fuel tank with nanoporous materials thus allows us to store three times the amount of NG into the tank than without it. A slightly larger tank would be needed to get the same driving distance as CNG, but this might be good enough.
Original Source Article
This article is the Young Minds version of a Perspective we have published in Energy and Environmental Science [6]. Our simulated data is available here: https://materialsproject.org/#search/porous
Glossary
Energy density (of a fuel): ↑ the amount of energy that can be extracted from one volume of fuel by burning it. The energy density determines how long a vehicle can drive with a full tank of fuel. Units: energy [mega Joules (MJ)] per volume [liter (L)], so MJ/L.
Liquefied natural gas (LNG): ↑ natural gas in liquid form, at a temperature of −162°C (−260°F) and atmospheric pressure.
Compressed natural gas (CNG): ↑ natural gas compressed to 200–250 times atmospheric pressure and at room temperature so it remains in its gaseous form.
Nanoporous material: ↑ a material that has small pores, <100 nm in size.
Adsorption: ↑ the process whereby molecules adhere to a surface. In the case of nanoporous materials, the walls of the pores form the surface to which gas molecules adsorb.
Metal-organic framework (MOF): ↑ a kind of nanoporous material in which metal nodes or clusters are combined with organic molecules called linkers to form the structure of the material.
Computer simulation: ↑ running a computer program that is designed to imitate and reproduce the behavior of a certain system. Here, our computer program imitates methane molecules entering, leaving, and moving in the pores of a nanoporous material.
References
[1] ↑ Makal, T., Li, J. R., Lu, W., and Zhou, H. C. 2012. Methane storage in advanced porous materials. Chem. Soc. Rev. 41:7761–79. doi: 10.1039/C2CS35251F
[2] ↑ Chui, S. S. Y., Lo, S. M. F., Charmant, J. P., Orpen, A. G., and Williams, I. D. 1999. A chemically functionalizable nanoporous material [Cu3(TMA)2(H2O)3]. Science 283(5405):1148–50. doi: 10.1126/science.283.5405.1148
[3] ↑ Eddaoudi, M., Kim, J., Rosi, N., Vodak, D., Wachter, J., O’Keeffe, M., et al. 2002. Systematic design of pore size and functionality in isoreticular MOFs and their application in methane storage. Science 295(5554):469–72. doi: 10.1126/science.1067208
[4] ↑ Kim, J., Martin, R. L., Rübel, O., Haranczyk, M., and Smit, B. 2012. High-throughput characterization of porous materials using graphics processing units. J. Chem. Theory Comput. 8(5):1684–93. doi: 10.1021/ct200787v
[5] ↑ Martin, R. L., Simon, C. M., Smit, B., and Haranczyk, M. 2014. In silico design of porous polymer networks: high-throughput screening for methane storage materials. J. Am. Chem. Soc. 136(13):5006–22. doi: 10.1021/ja4123939
[6] ↑ Simon, C. M., Kim, J., Gomez-Gualdron, D., Camp, J., Chung, Y., Martin, R. L., et al. 2015. The materials genome in action: identifying the performance limits to methane storage. Energy Environ. Sci. 8(4):1190–9. doi: 10.1039/C4EE03515A
