ملخص
تتغذى بعض الحيوانات من خلال اصطياد غيرها، ويُطلق على أي حيوان ضمن هذه الفئة اسم ''المفترس''. أما الحيوانات التي يتم اصطيادها وأكلها، فاسمها ''الفريسة''. برأيك ماذا سيحدث لو دخل مفترس إلى نظام بيئي عاشت فيه الفريسة سابقًا غير خائفة من اصطيادها؟ هل سيأكل المفترس الجديد كل الفرائس إلى أن تنقرض؟ في الواقع، ستدهشك العلاقة بين المفترس والفريسة إلى حد أكبر من ذلك. في هذا المقال، سنوضح شكل العلاقة بين المفترس والفريسة على امتداد الزمن وكيف يمكن للعلماء توقع تعدادات هذه الحيوانات في المستقبل، وكل ذلك باستخدام العمليات الرياضية الأساسية مثل الجمع والطرح والضرب.
لماذا علينا دراسة تعدادات الحيوانات؟
يحتاج العلماء إلى جمع المعلومات حتى يتسنى لهم فهم كيفية حماية البيئة والحيوانات التي تعيش في ظلها. ويستخدمون في بعض الأحيان الرياضيات لاختبار صحة نظرياتهم بشأن الحيوانات أو لمجرد محاولة توقع المستقبل.
يُطلق على هذه العملية اسم النمذجة الرياضية. ومن خلال نمذجة (وضع نماذج) للعلاقة بين المفترس والفريسة، يمكن للعلماء فهم كيفية تغير تعداد هذه الحيوانات على امتداد الزمن، كما تتسنى لهم معرفة متى يكون الحيوان معرضًا لخطر الانقراض. للنجاح في وضع نموذج رياضي، علينا جمع البيانات من البيئة المحيطة. في هذا المقال، سنبين كيفية استخدام بعض العمليات الرياضية الأساسية، مثل الجمع والطرح والضرب، لوضع نماذج للعلاقات التي يتم رصدها بين المفترس والفريسة في البيئة البرية.
البيانات هي أول ما نحتاجه!
الخطوة الأولى لتنفيذ نماذج جيدة هي جمع بيانات جيدة. ولنمذجة العلاقة بين المفترس والفريسة، سنستخدم بيانات التعدادات (سجلات بأعداد الحيوانات الموجودة) التي جمعتها شركة قامت على اصطياد الحيوانات المفترسة والفرائس على حد سواء للحصول على فرائها في القرنين التاسع عشر والعشرين. وهذه الشركة هي هدسن باي وقد أنشأت سجلات سنوية بأعداد الفراء التي جمعتها من حيوانات الوشق الثلجي والأرانب البرية الثلجية. يعرض شكل 1 البيانات التي تملكها الشركة حول عدد فراء هذه الحيوانات. نستنتج من هذا العدد تعدادات هذه الحيوانات، كما يمكننا من خلاله تصوّر العلاقة بين المفترس والفريسة بشكل عملي. ففي بعض السنوات مثل 1927، كان عدد حيوانات الوشق (المفترسة) أكبر من عدد الأرانب البرية (الفرائس)، بينما نجد في سنوات أخرى، مثل 1932 أن عدد الأرانب البرية كان أكبر من عدد حيوانات الوشق.
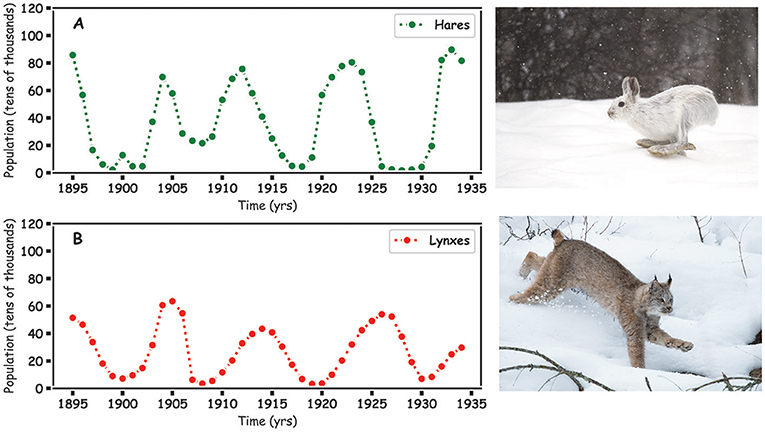
- شكل 1 - (A) عدد فراء الأرانب البرية التي تم جمعها (عشرات الآلاف) على امتداد الزمن.
- (B) عدد فراء حيوانات الوشق التي تم جمعها (عشرات الآلاف) على امتداد الزمن، بناءً على بيانات شركة هدسن باي في الفترة من 1895 إلى 1935.1
مدلول بيانات شركة هدسن باي
إن الارتفاع والانخفاض في التعدادات المسجلة للأرانب البرية وحيوانات الوشق على امتداد الزمن يدل على وجود علاقة بين الحيوانين، وهذا مفهوم لأن الوشق يلتهم الأرنب البري. في شكل 1، هل يمكنك رؤية أن تعدادات حيوانات الوشق والأرانب البرية تنخفض وترتفع في الوقت نفسه تقريبًا؟
عندما يزيد عدد حيوانات الوشق، فإنها تلتهم المزيد من الأرانب البرية، ما يؤدي إلى انخفاض تعدادها. وعندما يقل تعداد الأرانب البرية، لن تجد حيوانات الوشق ما يكفي من الغذاء، مما سيؤدي بدوره إلى انخفاض تعدادها، فيزيد تعداد الأرانب البرية مرة أخرى، وهكذا تستمر هذه الدورة من الارتفاع والانخفاض في التعدادات. في حالة التوازن بين تعدادات الحيوانات المفترسة والفرائس، فإنها ستنخفض وترتفع على امتداد الزمن، بينما تطارد بعضها البعض في دورة الحياة. السؤال الذي يطرحه هنا عالم الرياضيات هو: ''هل يمكنني شرح هذا الأمر باستخدام الجمع والطرح والضرب، وهل يمكنني توقع التعدادات في المستقبل؟''
شرح العلاقة من خلال النماذج الرياضية
يستخدم علماء الرياضيات المعادلات التفاضلية والبيانات لوصف ما يرصدونه في العالم. وقد وُصفت العلاقة بين المفترس والفريسة لأول مرة باستخدام المعادلات التفاضلية، وقام بهذا المجهود عالمان هما ''لوتكا'' [1] و''فولتيرا'' [2]. فقد أرادا الاستعانة بالرياضيات لشرح الارتفاع والانخفاض الملحوظين في العلاقة العامة بين المفترس والفريسة.
تبدو المعادلات أحيانًا شديدة التعقيد، ولكننا ننظر إليها على أنها مجرد وسيلة لوصف مدى وسبب تغير التعدادات. وقد أثبت عالم رياضيات مشهور اسمه ''ليونهارت أويلر'' (1707-1783) أنه يمكن صياغة المعادلات التفاضلية كعمليات جمع وطرح، بالإضافة إلى القليل من عمليات الضرب. ومن خلال المعادلات التفاضلية، يمكن وضع نموذج لتعدادات الوشق (المفترس) والأرنب البري (الفريسة) باستخدام بيانات شركة هدسن باي. نستخدم البيانات الأصلية بواسطة طرق رياضية [3] من أجل تقدير قيم معدّل النمو (rgrowth) ومعدل الوفيات (rdeath) ومعدل الافتراس (reaten) ومعدل الغذاء المطلوب (rfood)، ومن خلال ذلك يمكننا توقع تعدادات حيوانات الوشق والأرانب البرية.
نمذجة تعداد الأرانب البرية الثلجية
عندما يصيغ علماء الرياضيات المعادلات، يتأملون العالم المحيط بهم. والآن لنفكر فيما يتعرض له تعداد الأرانب البرية على امتداد الزمن. إذا انعدم وجود حيوانات الوشق، يمكن حساب تعداد الأرانب البرية في المستقبل (HF) بجمع تعداد الأرانب البرية الحالي (HC) مع حاصل طرح الوفيات من المواليد، أي معدل النمو (rgrowth). سيعتمد عدد المواليد والوفيات على عدد الأرانب البرية الحية الآن، وبالتالي سنضرب rgrowth في HC (شكل 2A).

- شكل 2 - (A) المعادلات المُستخدمة لتوقع تعداد الأرانب البرية في المستقبل في حال انعدام وجود حيوانات الوشق، وتدل حلولها على نمو أسي.
- (B) المعادلات المستخدمة لتوقع تعداد حيوانات الوشق في المستقبل في حال انعدام وجود الأرانب البرية، وتدل حلولها على اضمحلال أسي. (C) معادلات تعدادات الأرانب البرية وحيوانات الوشق في حالة تفاعلها مع بعضها. نرى في الحلول أن تعدادات الأرانب البرية وحيوانات الوشق متقلبة وغير ثابتة على حد سواء.
والآن لنستخدم بيانات شركة هدسن باي ونضع الأرقام في المعادلة. بما أن البيانات تبدأ في عام 1895 حيث كان تعداد الأرانب البرية 85، فإن HC = 85 أرنبًا بريًا. ويكون معدل نمو تعداد الأرانب البرية كالتالي: rgrowth = 0.9 في العام. وبما أن قيمة rgrowth موجبة، فنحن نتوقع أن يزيد التعداد في المستقبل. وهذا يعطينا تعداد الأرانب البرية لاحقًا (HF) في عام 1896:
HF = HC + (rgrowth × HC)
HF = 85 + (0.9 × 85) =161.5.
نتوقع من ذلك أن تعداد الأرانب البرية المستقبلي سيكون 161.5. وإذا استمر هذا النمو في التعداد، ستكون الأرانب البرية موجودة في العالم كله، وهذا ما يُسمى بالنمو الأسي (شكل 2A).
نمذجة تعداد حيوانات الوشق الثلجي
لنتناول الآن ما يحدث لتعداد حيوانات الوشق على امتداد الزمن. إذا اختفت الأرانب البرية، لن تجد حيوانات الوشق ما تقتات عليه، وبالتالي سينخفض تعدادها. سنستخدم عملية الطرح لوضع نموذج لهذا الأمر. العدد المستقبلي لحيوانات الوشق (LF) يساوي العدد الحالي لحيوانات الوشق (LC) مطروحًا منه حاصل ضرب معدل الوفيات rdeath في العدد الحالي لحيوانات الوشق (شكل 2B).
في عام 1895، كان تعداد حيوانات الوشق يساوي 51، وعند توفيق البيانات، يكون معدل الوفيات كالتالي: rdeath = 0.25. بذلك يكون ناتج المعادلة:
LF = LC – (rdeath × LC)
LF = 51 – (0.25 × 51) = 38.25.
من خلال حساباتنا، نتوقع أن يصل تعداد حيوانات الوشق في عام 1896 إلى 38.25. وهذا اسمه اضمحلال أسي، وإذا استمر في الحدوث، فستنقرض حيوانات الوشق (شكل 2B).
نمذجة التفاعل بين الأرانب البرية وحيوانات الوشق
عرفنا أن تعداد الأرانب البرية يزيد وتعداد حيوانات الوشق ينخفض، كلاً على حدة. ولكن ما الذي نعرفه حول شكل التفاعل بينهما؟ تأكل حيوانات الوشق الأرانب البرية، فينخفض تعدادها، ولذا سنستخدم عملية الطرح لنمذجة هذه العلاقة. نحتاج إلى مصطلح للتعبير عن معدل الافتراس وهو reaten، وتعتمد قيمته على التعدادين الحاليين لكل من حيوانات الوشق (المفترسة) والأرانب البرية (الفرائس) الحية. سنضرب إذًا reaten في LC و HC.
باتباع المنطق نفسه، تتغذى حيوانات الوشق على الأرانب البرية، لذا نستخدم عملية الجمع في معادلة حيوانات الوشق ونضرب التعداد الحالي للأرانب البرية في التعداد الحالي لحيوانات الوشق في معدل الغذاء المطلوب rfood (شكل 2B).
ولا تتغير القيم التالية: HC = 85 أرنبًا بريًا، وrgrowth = 0.9 وLC = 51 حيوان وشق، وrdeath = 0.25. بناءً على البيانات، نجد أن معدل الافتراس (reaten) يساوي 0.024 ومعدل الغذاء المطلوب (rfood) يساوي 0.005. وبوضع هذه الأرقام في المعادلة لتوقع عدد الأرانب البرية في المستقبل، نحصل على:
HF = HC + (rgrowth × HC) – (reaten × LC × HC)
HF = 85 + (0.9 × 85) – (0.024 × 85 × 51) = 59.24
أما معادلة توقع عدد حيوانات الوشق في المستقبل، فتكون كالتالي:
LF = LC – (rdeath × LC) + (rfood × LC × HC)
LF = 51 – (0.25 × 51) + (0.005 × 51 × 85) = 59.925.
يتوقع النموذج الخاص بنا (كلتا المعادلتين السابقتين) انخفاضًا في تعداد الأرانب البرية وارتفاعًا في تعداد حيوانات الوشق في عام 1896، كما هو مبين في شكل 3 من خلال السهمين الأخضر والأحمر.
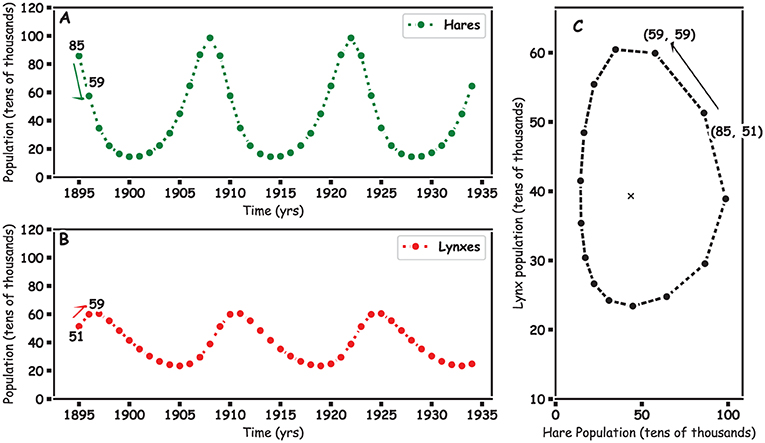
- شكل 3 - أُعدت نماذج لتعدادات الأرانب البرية وحيوانات الوشق باستخدام المعادلات وبيانات شركة هدسن باي التي جُمعت في الفترة من 1895 إلى 1935.
- (A) نموذج تعداد الأرانب البرية. (B) نموذج تعداد حيوانات الوشق. يعرض هذان المخططان الارتفاع والانخفاض المرصودين في البيانات الحقيقية في شكل 1. (C) مدى التغير في تعداد حيوانات الوشق عند المقارنة مع تعدادات مختلفة للأرانب البرية. يشير رمز x إلى متوسط تعداد حيوانات الوشق والأرانب البرية، وهو المركز الذي يدور حوله التعدادان. تشير الأسهم والأرقام إلى الحسابات المستندة إلى البيانات من العام 1895 إلى 1896.2
ولتوقع التغيرات التي ستطرأ على التعدادين في العام التالي وهو 1897، سنضع قيمتي HF وLF محل HC وLC في المعادلتين الجديدتين. وفي كل مرة نقوم بهذا، نحصل على قيم جديدة، وكل قيمة تمثل نقطة في الرسوم البيانية في شكل 3.
التمثيل البياني للعلاقة بين المفترس والفريسة
باستخدام المعادلات السابقة وبعض التعلميات البرمجية على الكمبيوتر [4]، يمكننا محاكاة تعدادي الأرانب البرية وحيوانات الوشق وإعداد بياناتنا التي توضح مدى تطور العلاقة بين المفترس والفريسة بمرور الزمن (شكل 3).
يمكن أيضًا توضيح العلاقة بين نوعين من خلال إعداد مخططات تظهر مدى تغير تعداد الأرانب البرية (شكل 3C) وتعداد حيوانات الوشق (المحور الصادي) بسبب بعضهما البعض (الشكل 3C). يشير الرمز x في المنتصف إلى متوسط تعداد الأرانب البرية (39) وتعداد حيوانات الوشق (45)، ويُعرف أيضًا باسم نقطة التوازن. وتدور تعدادات الأرانب البرية وحيوانات الوشق (مع كل ارتفاع وانخفاض لها) في فلك هذا المتوسط، مما يعطينا مخططًا لدورة الحياة. يشبه الأمر قليلاً دوران الأرض حول الشمس. فالتعدادات تستمر في الدوران، ما يمثل ارتفاعها وانخفاضها بمرور الزمن. وفي النظام البيئي المتوازن، مثل النظام الذي تمت نمذجته هنا، يظل مسار الدوران مستقرًا، ولكن إذا بدأ في الاتساع أو التقلص، قد تكون هذه علامة مبكرة على حدوث تغير.
حدث مثال على هذا التغير في عام 1995 عندما أعيدت الذئاب إلى متنزه يلوستون الوطني. فقد أدى ذلك إلى بعض الآثار غير المتوقعة على النظام البيئي المحيط.3 بناءً على هذه الملاحظات المدهشة والعمليات الرياضية المشابهة لما استخدمناه هنا، طوّر ''جودمان'' وزملاؤه لعبة كمبيوتر لبناء نظام بيئي متوازن.4
عدم دقة النماذج
عندما يحاول علماء الرياضيات وصف شيء معقد، يحاولون تبسيط الأمور، تمامًا كالمعادلات المبينة هنا أيضًا. معنى التبسيط أن التوقعات وعمليات المحاكاة لا تتبع بشكل تام البيانات الأصلية. إليك بعض المعلومات التي أغفلناها في نموذجنا:
- لا تتعرض الأرانب البرية الثلجية للافتراس من حيوانات الوشق فقط.
- لا تصطاد حيوانات الوشق الثلجي الأرانب البرية الثلجية فحسب، بل تصطاد أيضًا الأسماك والسناجب.
- في نموذجنا، لا ينفد الطعام لدى الأرانب البرية الثلجية، ولكن هذا الأمر ليس صحيحًا في الشتاء.
- ماذا عن صائدي الفراء من البشر الذين يطاردون حيوانات الوشق والأرانب البرية على حد سواء؟
حتى تنطبق المعادلات على كل المواقف الأخرى، علينا تضمين معادلات إضافية وإجراء المزيد من عمليات الجمع والطرح. وإذا أتيح لدينا كل البيانات، يمكننا نمذجة التعدادات المستقبلية بشكل ممتاز. صحيح أن علماء الرياضيات يلجئون إلى التبسيط، ولكن جهودهم في نمذجة تعدادات الأرانب البرية وحيوانات الوشق تستحق التقدير.
ما الاستخدامات المحتملة الأخرى لهذا النموذج؟
إذا بدلت كلمتي ''الوشق الثلجي'' إلى ''القرش'' و''الأرنب البري الثلجي'' إلى ''الأسماك'' في هذا النموذج، تظل تنطبق المعادلات الرياضية في وجود البيانات المناسبة [2]، بل ويمكنك استخدام المعادلات نفسها وتغيير كلمة ''الوشق'' إلى ''كائن الزومبي'' و''الأرنب البري'' إلى ''الإنسان''. ويمكن توسيع نطاق العلاقة بين المفترس والفريسة لتتجاوز عالم الحيوانات واستخدامها في نمذجة كيفية تفاعل الشركات وكيفية حدوث التفاعلات الكيميائية وكيفية انتشار الفيروسات. يمكنك قراءة المزيد حول استخدام الرياضيات لتوقع انتشار الفيروسات في مقال آخر نُشر على موقع فرونتيرز للعقول الشابة من خلال النقر هنا [5].
الملخص
لوضع نماذج للعالم الواقعي، يحتاج علماء الرياضيات أولاً إلى بيانات جيدة. ومعنى هذا أن جمع المعلومات من البيئة المحيطة في غاية الأهمية للعلماء ودعاة حماية البيئة وصائدي الفراء. وباستخدام البيانات، يمكننا رصد أنماط في العلاقات، ثم استخدام الرياضيات لإعادة إنشاء هذه الأنماط وتوقع البيانات المستقبلية، ما يتيح لنا تمثيل وتوقع مستقبل هذه العلاقات. ويمكن أن تساعدنا هذه التوقعات في الحفاظ على توازن الأنظمة البيئية. نأمل أن يكون هذا المقال قد ساعدك على إدراك أن العمليات الرياضية البسيطة مثل الجمع والطرح والضرب والتفكير الذكي هما كل ما نحتاجه لنمذجة وتوقع تعدادات المفترسات والفرائس وغير ذلك الكثير.
إقرار
قام مجلس البحوث الأيرلندي بتمويل هذا المقال (GOIPG/2020/943).
مسرد للمصطلحات
المعادلات التفاضلية (Differential Equations): ↑ معادلات تصف مدى تغير التعدادات على امتداد الزمن أو تشرح العديد من العمليات الأخرى، بما في ذلك آلية تحليق الطائرة المروحية أو كيفية دوران الكواكب حول نجم ما أو طريقة تدفق الدم في أوردتنا.
التقديرية (Estimate): ↑ قيمة قريبة بما يكفي من الإجابة الصحيحة، ويتم التوصل إليها في العادة بناءً على بعض المعلومات التي لديك بشأن النظام أو من خلال إجراء عملية حسابية.
معدّل النمو (Growth Rate): ↑ معدل النمو هو زيادة تعداد الأرانب البرية عند انعدام وجود أي حيوانات مفترسة. ويمكن تقديره من البيانات بطرح عدد المواليد من الوفيات.
معدل الوفيات (Death Rate): ↑ هو انخفاض تعداد حيوانات الوشق على امتداد الزمن نتيجة انعدام الغذاء. ويمكن التوصل إليه من خلال طرح عدد الوفيات من المواليد.
معدل الافتراس (Eat Rate): ↑ هو عدد الأرانب البرية التي اصطادتها والتهمتها حيوانات الوشق.
معدل الغذاء المطلوب (Food Rate): ↑ هو عدد الأرانب البرية التي تحتاج حيوانات الوشق إلى التهامها لتبقى على قيد الحياة.
النمو الأسي (Exponential Growth): ↑ نمو يتسم بالثبات والسرعة.
نقطة التوازن (Equilibrium Point): ↑ نقطة التوازن في التعدادين. عندما يكون النظام في حالة توازن، نصفه بأنه مستقر.
إقرار تضارب المصالح
يعلن المؤلفون أن البحث قد أُجري في غياب أي علاقات تجارية أو مالية يمكن تفسيرها على أنها تضارب محتمل في المصالح.
الحواشي
1. ↑يمكن العثور على رابط نسخة متحركة من الشكل هنا
2. ↑يمكن العثور على رابط إلى نسخة متحركة من الشكل هنا
3. ↑يمكنك المشاهدة هنا: Sustainable Human 2014
4. ↑يمكن اللعب على هذا الرابط: https://ecobuildergame.org
المراجع
[1] ↑ Lotka, A. J. 1920. Analytical note on certain rhythmic relations in organic systems. Proc Natl Acad Sci USA. 6:410–5.
[2] ↑ Volterra, V. 1926. Fluctuations in the abundance of a species considered mathematically. Nature. 118:558–60.
[3] ↑ de Silva, B. M., Champion, K., Quade, M., Loiseau, J. C., Kutz, J. N., and Brunton, S. L. 2020. PySINDy: a python package for the sparse identification of nonlinear dynamics from data. arXiv Preprint arXiv:2004.08424.
[4] ↑ Butler, J. S., and Brady, R. M. 2020. Predator Prey Code for Young-Minds. GitHub. Available online at: https://github.com/john-s-butler-dit/Predator-Prey-for-Young-Minds
[5] ↑ Brooks, H. Z., Kanjanasaratool, U., Kureh, Y. H., and Mason. P. 2021. Disease detectives: using mathematics to forecast the spread of infectious diseases. Front Young Minds. 9:577741. doi: 10.3389/frym.2020.577741
