תַקצִיר
נניח שאתם בדרך לבית הספר ומגיעים לתחנת אוטובוס. כמה זמן תצטרכו לחכות לאוטובוס הבא שיגיע? באופן מפתיע, זהו זמן רב יותר – ייתכן שהרבה יותר ארוך – ממה שהייתם מנחשים מתוך התבוננות בלוח הזמנים של האוטובוס. לתופעה הזו, שנקראת פָּרָדוֹקְס זְמַן הַהַמְתָּנָה, יש מקור מתמטי טהור. במאמר זה נחקור את התופעה, נסביר מדוע היא מתרחשת ונדון בכמה מהשלכותיה (מעבר לאפשרות של איחור לבית הספר).
כמה זמן תצטרכו לחכות לאוטובוס הבא?
נניח שאתם גרים בעיר ולוקחים אוטובוס כדי להגיע לבית הספר. מאחר שאוטובוסים מגיעים לעיתים קרובות בשכונתכם, אולי אינכם צריכים להקדיש תשומת לב מיוחדת ללוח הזמנים של האוטובוס. ייתכן שאתם פשוט הולכים לתחנת האוטובוס הקרובה, ועולים על האוטובוס הבא (ראו איור 1A). אולם, אם אתם מגיעים לתחנה ואין לכם מושג מתי יגיע האוטובוס הבא, כמה זמן תצטרכו להמתין לו?
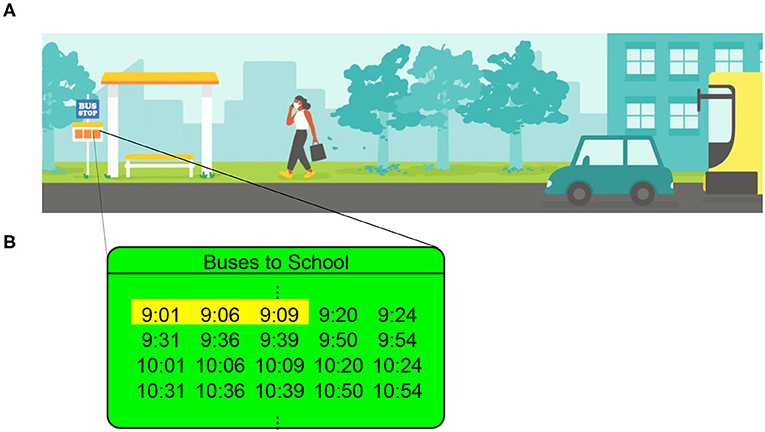
- איור 1 - שיעור זמן ההמתנה.
- (A) אתם מגיעים לתחנת האוטובוס כדי להמתין לאוטובוס הבא. (B) אתם מסתכלים על לוח הזמנים ורואים שישנם 10 אוטובוסים במהלך כל שעה. זה ממוצע של אוטובוס אחד בכל 6 דקות. שלושת האוטובוסים הראשונים אחרי השעה 9:00 מיועדים להגיע בשעות 9:01, 9:06 ו-9:09 (מודגשים בצהוב בלוח הזמנים שבאיור). הזמנים שבין-אירועים, כלומר הזמנים שבין אוטובוסים עוקבים, הם 5 דקות (בין האוטובוסים הראשון והשני), ו-3 דקות (בין האוטובוסים השני והשלישי). [פאנל A צויר על ידי Iris Leung].
נניח ש-10 אוטובוסים מגיעים במהלך כל שעה (ראו איור 1B), כך שאוטובוס אחד מגיע כל 6 דקות בממוצע. אם האוטובוס האחרון עוזב ממש לפני שאתם מגיעים לתחנה, ייתכן שתצטרכו להמתין 5 או 6 דקות לאוטובוס הבא. אם האוטובוס האחרון עוזב כמה דקות לפני שאתם מגיעים לתחנה, ייתכן שהאוטובוס הבא יגיע עוד דקה בלבד, או אולי 4 דקות, או אולי 2 דקות? ניחוש מושכל עבור ''זמן ההמתנה'' הוא 3 דקות – מחצית הזמן בין אוטובוסים בממוצע. אך ההנמקה הזו אינה נכונה. למעשה, עליכם לחכות יותר מ-3 דקות. זמן ההמתנה הצפוי שלכם יכול להיות אפילו ארוך יותר מ-6 דקות. התופעה הזו נקראת פרדוקס זמן ההמתנה [2 ,1]. פרדוקס הוא משהו שנדמה כבלתי הגיוני, אך למעשה מתברר כנכון. אנשים רבים חושבים כי פרדוקס זמן ההמתנה הוא פרדוקס מאחר שזמן ההמתנה הטיפוסי בתחנת האוטובוס ארוך ממחצית פרק הזמן שבין הַגָּעַת אוטובוסים (שהוא 3 דקות בדוגמה לעיל). פרדוקס זמן ההמתנה הוא תופעה מתמטית, ואין לה קשר לאוטובוסים. מהי תופעה זו וכיצד היא מתעתעת בנו? המשיכו לקרוא כדי לגלות!
מדוע פרדוקס זמן ההמתנה מתרחש?
כדי להבין זאת, התבוננו בלוח הזמנים של האוטובוס באיור 2A. בלוח הזמנים הזה, שהוא פשוט יותר מלוח הזמנים שבאיור 1, אוטובוסים מגיעים במרווחים של 4 דקות או של 12 דקות. בלוח הזמנים המקורי של האוטובוס, באיור 1B, יש זמנים שנראים לא עקביים, וישנם מרווחים שונים בין זְמַנֵּי הַגָּעַת האוטובוס. באופן כללי, כשסיטואציה נראית מורכבת, כדאי לְפַשֵּׁט אותה לפני שמבצעים הנמקה מתמטית – אנשים העוסקים בתחום המתמטיקה עושים זאת כל הזמן. פרדוקס זמן ההמתנה מתרחש בלוח הזמן המפושט של האוטובוס, וההפשטה מקלה על ההבנה של מה מתרחש.
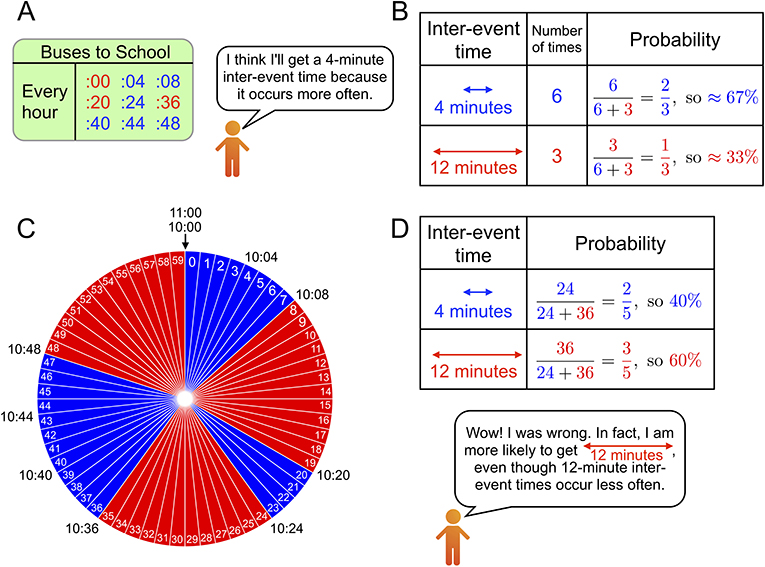
- איור 2 - השוואה בין ניחוש נאיבי של זמן המתנה ממוצע לבין זמן ההמתנה הממוצע בפועל.
- (A) לוח זמנים מפושט של אוטובוס. (B) ניחוש נאיבי לגבי ההסתברויות של קבלת זמנים שבין-אירועים באורכים של 4 דקות ושל 12 דקות. ניחוש זה מתבסס על ההנחה השגויה שלפיה זמן של 4 דקות סביר יותר מזמן של 12 דקות מאחר שהוא מתרחש לעיתים תכופות יותר. (C) הַצָּגַת זמנים שבין-אירועים לאורך שעה אחת בתור דיאגרמת עוגה יכולה לסייע לנו להבין מדוע זה לא נכון. (D) ההסתברות המעשית של קבלת זמנים בין-אירועים באורך 12 דקות גדולה יותר מההסתברות של קבלת זמנים בין-אירועים באורך 4 דקות מאחר שישנן 36 חתיכות אדומות לעומת 24 חתיכות כחולות בלבד בדיאגרמת העוגה ב-(C).
רעיון מרכזי שעלינו להביא בחשבון הוא ה הזמן שבין-אירועים, שהוא הזמן שבין שני אוטובוסים עוקבים. לוח הזמנים שבאיור 2A מצביע על כך שבכל שעה שישה אוטובוסים מגיעים מייד לאחר זמן בין-אירועים של 4 דקות (בכחול), ושלושה אוטובוסים מגיעים מייד אחרי זמן בין-אירועים של 12 דקות (באדום). בתרחיש שלנו, היזכרו בכך שהגעתם לתחנת האוטובוס בלי לדעת מתי יגיע האוטובוס הבא. בשפה של תורת ההסתברות, אנו אומרים שאתם מגיעים לתחנת האוטובוס בזמן שנבחר אופן אחיד באקראי. האם אתם חושבים שסביר יותר לחוות זמן בין-אירועים של 4 דקות או של 12 דקות? אם אתם מקבלים זמן המתנה של 4 דקות, לא תמתינו זמן רב לאוטובוס הבא. אך אם אתם מקבלים זמן המתנה של 12 דקות, אתם עשויים להמתין זמן רב. כפי שציינו לעיל, שישה זמנים בין-אירועים הם באורך של 4 דקות, ושלושה זמנים בין-אירועים הם באורך של 12 דקות.
ניתוח המקרה לדוגמה
חשבו על זה כך: אולי סביר שתקבלו זמן בין-אירועים של 4 דקות מאחר שישנם שישה כאלה בכל שעה, אולם זמנים בין-אירועים של 12 דקות מתרחשים רק שלוש פעמים בשעה. הראשון מתרחש בהסתברות של 6/(6 + 3) = 2/3, שזה בערך 0.67, ולכן המצב הזה מתרחש 67% מהזמן (ראו איור 2B). השני מתרחש בהסתברות של 3/(6 + 3) = 1/3, ולכן המצב הזה מתרחש כ-33% מהזמן. לרוע המזל, זוהי תקוות שווא. הגעה לתחנת האוטובוס באופן אחיד באקראי היא כמו סיבוב של גלגל עם המספרים 0 עד 59 על כל ''פיסה'' של הגלגל (כך שישנן 60 פיסות בסך הכול), עצירתו עם אצבעכם והתבוננות בחתיכה שבה האצבע נוגעת. אם אצבעכם מצביעה על 33, זה אומר שתגיעו לתחנת האוטובוס ב-10:33. במקרה הזה, תצטרכו להמתין 3 דקות לאוטובוס הבא, אשר מגיע ב-10:36. הגלגל מספק דרך לסייע לנו להבין את הכוונה ב''אחידות באקראי''. כל דקה על הגלגל צבועה, כאשר כחול מתייחס לזמן בין-אירועים של 4 דקות, ואדום מתייחס לזמן של 12 דקות. באיור 2C, אנו רואים שישנן 24 דקות כחולות ו-36 דקות אדומות. מהתמונה הזו, ניתן גם לראות שיש לנו סבירות גדולה יותר לקבל זמן בין-אירועים של 12 דקות (מתרחש בהסתברות של 0.6) ביחס לזמן של 4 דקות (מתרחש בהסתברות של 0.4) (ראו איור 2D).
אף על פי שרק שליש מתוך תשעת הזמנים שבין-אירועים (אם כן ישנהּ הסתברות של 1/3 בקבלת אחד) הם באורך של 12 דקות, עדיין סביר יותר (בפרט, ההסתברות היא 0.6) לקבל אחד מאלה מאשר אחד מהזמנים בין-אירועים שאורכם 4 דקות. התשובה לכך טמונה בעובדה פשוטה: זמן ארוך בין-אירועים הוא ארוך, וזמן קצר הוא קצר. זמן ארוך בין-אירועים תופס 12 מספרים בגלגל המשחק, אך הזמן הקצר תופס רק 4 מספרים. שלושת הזמנים הארוכים שבין-אירועים מכסים 12 × 3 = 36 מתוך 60 הדקות. בניגוד לכך, ששת הזמנים הקצרים יחד מכסים רק 4 × 6 = 24 דקות. כתוצאה מכך, נדירותו של זמן בין-אירועים בלוח הזמנים של האוטובוס לא מורה על כך שנדיר לפגוש את אותו הזמן בין-אירועים. על ידי ביצוע חישובים מסוימים עם לוח הזמנים של האוטובוס באיור 2A, אנו רואים שהניחוש הנאיבי עבור כמות הזמן שאתם צריכים לצפות להמתין (מחצית הממוצע של הזמן שבין-אירועים) הוא 3 דקות ו-20 שניות, אך זמן ההמתנה הממוצע המעשי הוא 4 דקות ו-24 שניות. בלוח הזמנים באיור 1B, הניחוש הנאיבי עבור זמן ההמתנה הממוצע הוא 3 דקות, וזמן ההמתנה הממוצע בפועל הוא 3 דקות ו-40 שניות. נניח שכל הזמנים שבין-אירועים אורכים 6 דקות, כלומר שהאוטובוסים מגיעים כל 6 דקות בדיוק. במקרה הזה, כבר אין פרדוקס זמן המתנה, מאחר שהניחוש הנאיבי וזמן ההמתנה הממוצע בפועל אורכים שניהם 3 דקות. כדי שפרדוקס זמן ההמתנה יתרחש, נדרש שתהיה לנו תערובת של לפחות שני זמנים בין-אירועים, כמו למשל 4 דקות ו-12 דקות.
יישומים והרחבות
פרדוקס זמן ההמתנה תָּקֵף להרבה יותר מאשר זמני המתנה לאוטובוס. זמנים בין- אירועים הם בעלי חשיבות בסיטואציות רבות. חשבו על ''אירוע'' של שיחה עם חֲבֵרָה לכיתה בבית הספר. הזמנים שבין-אירועים הם כמות הזמן שבין שיחות עם חברי הכיתה (ראו איור 3A). זמן אחד בין-אירועים יכול להיות 2 דקות, והזמן הבא יכול להיות 11 דקות. בפעילויות חברתיות, שלא כמו לוחות זמנים של אוטובוסים, לעיתים קרובות ישנהּ שׁוֹנוּת רבה בזמנים שבין-אירועים. באיור 3B, אנו מראים היסטוגרמה של זמנים בין- אירועים עבור תלמידים בבית ספר בצרפת [3]. בהיסטוגרמה, אנו מציינים את הפעמים משמאל לימין בסדר עולה. הגובה של כל עמודה בהיסטוגרמה מצביע על מספר הפעמים שכל זמן בין-אירועים מתרחש. מרבית הזמנים בין-אירועים הם קצרים (כמו למשל 20 או 40 שניות), אך חלק קטן מהם הוא ארוך (כמו למשל בין 200 ל-400 שניות).
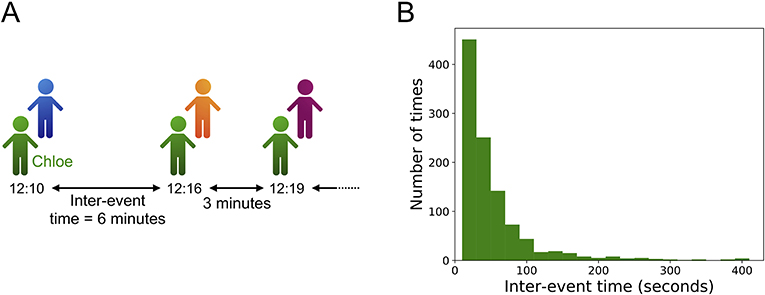
- איור 3 - זמנים בין-אירועים עבור תלמידים שמתחברים בבית הספר.
- (A) הזמנים בין-אירועים עבור תלמידה בשם Chloe. Chloe מדברת עם שלושה תלמידים שונים, בזמנים בין-אירועים של 6 דקות ושל 3 דקות. (B) היסטוגרמה של זמנים בין-אירועים עבור תלמידה בבית הספר בצרפת. הדוגמה הזו מגיעה מסֶט הנתונים ''Primary School'' של פרויקט SocioPatterns [3]. בחרנו את התלמידה עם מספר האירועים הגדול ביותר, וחישבנו את הזמנים שבין-אירועים של התלמידה. העמודות באיור זה מצביעות על מספר הזמנים בין-אירועים שהתרחשו בכל אורך זמן עבור אותה התלמידה. ההיסטוגרמה מראה שישנהּ שׁוֹנוּת גדולה בזמנים שבין-אירועים. מרביתם קצרים, אך חלקם ארוכים מאוד.
בדוגמה של פרדוקס זמן ההמתנה עם אוטובוסים, ראינו שאפילו אם ישנם רק שלושה זמנים ארוכים בין-אירועים מתוך תשעה זמנים בין-אירועים סך הכול, סביר יותר שנקבל את אחד מהזמנים הארוכים מאשר את אחד מהזמנים הקצרים. זוהי דוגמה של דגימה מֻטָּה. דוגמה מפורסמת אחרת של דגימה מוטה היא פרדוקס החברוּת [5 ,4]. לפי פרדוקס זה, לחבריכם יש לרוב יותר חברים מאשר לכם. אך אין סיבה להיות מתוסכלים, מאחר שגם זו תופעה מתמטית טהורה. אם יש לכם 20 חברים בבית הספר, רבים מהם צפויים להיות אנשים פופולריים. לדוגמה, אם לאליס יש חבר אחד בלבד, הסבירות שאתם חברים שלה היא קטנה; סביר יותר שזה מישהו אחר. בניגוד לכך, אם בוב חבר של מחצית התלמידים בבית ספרכם, סביר ביותר שאתם תהיו אחד מחבריו של בוב.
המתנה לאוטובוס הבא וספירת כמות החברים עשויות להיראות לא קשורות זו לזו. אך מנקודת מבט מתמטית, ככל הנראה יהיה לכם חבר אחד כמו בוב מאותה סיבה בסיסית לכך שסביר שתתפסו אוטובוס אחרי זמן ארוך בין-אירועים. נניח שישנם שישה תלמידים שלכל אחד מהם יש 4 חברים, ושלושה תלמידים שלכל אחד מהם יש 12 חברים. אם אתם חברים של תלמיד אחד בלבד מתוך תשעת התלמידים האלה, סביר שחברכם יהיה אדם עם 12 חברים, אף על פי שישנם רק שלושה תלמידים עם 12 חברים מתוך 6 + 3 = 9 תלמידים. המספרים האלה זהים בדיוק לאלה שהשתמשנו בהם באיור 2 כדי להדגים את פרדוקס זמן ההמתנה. זה ממחיש כי לפרדוקס זמן ההמתנה ולפרדוקס החברוּת יש אותו מקור מתמטי. שניהם תוצר של דגימה מוטה.
הֲבָנַת פרדוקס זמן ההמתנה שימושית בסיטואציות רבות, כמו למשל הבנה עד כמה מהר מחלה מתפשטת באוכלוסייה [6]. בקורסים באוניברסיטה ובמחקר מדעי, פרדוקס זמן ההמתנה מופיע לעיתים קרובות בתחומים כמו תורת ההסתברות, תורת התורים וניתוח רשתות. כפי שראינו, מתמטיקה מספקת דרך לְאַחֵד רעיונות שונים ולראות מתי הם קשורים זה לזה, מה שנכון לא רק לגבי פרדוקס זמן ההמתנה ופרדוקס החברות, אלא גם לגבי דברים רבים אחרים.
מילון מונחים
פרדוקס זמן ההמתנה (Waiting-Time Paradox): ↑ תופעה מתמטית שעוסקת בזמנים שנראים בלתי הגיוניים, אך הם למעשה נכונים. בפרדוקס זמן ההמתנה, אם אירוע מתרחש בזמן שאותו אנו בוחרים באופן אחיד באקראי, זמן ההמתנה הממוצע עד לאירוע הבא ארוך יותר ממחצית הזמן שבין-אירועים. פרדוקס זמן ההמתנה נקרא גם ''פרדוקס האוטובוס'' ו''פרדוקס הבקרה''.
זמן בין-אירועים (Inter-Event Time): ↑ כמות הזמן שבין שני אירועים עוקבים, כמו למשל ההגעות של שני אוטובוסים לתחנת האוטובוס, או שתי שיחות של אדם עם אדם אחר.
תורת ההסתברות (Probability Theory): ↑ תחום במתמטיקה שעוסק בנושאים שקשורים ל''הסתברות'', שהיא תיאור מספרי של הסבירות של תוצאה להתרחש. ''התפלגות הסתברותית'' היא פונקציה מתמטית שנותנת את ההסתברויות של כל התוצאות האפשריות של משהו.
אופן אחיד באקראי (Uniformly at Random): ↑ התפלגות הסתברותית שבה לכל תוצאה אפשרית יש סיכוי זהה להתרחש.
היסטוגרמה (Histogram): ↑ דיאגרמה שמראה את השכיחות של פריטים בכמה טווחי מספרים במטרה להשוות את שכיחות הפריטים בכל טווח. היסטוגרמה יכולה להראות למשל ילדים בטווח הגילים 4-0, 9-5, 14-10, וכן הלאה. גובה העמודה עבור טווח הגילים 14-10 שנים, לדוגמה, מצביע על מספר האנשים שהם בטווח גילים זה.
דגימה מוטה (Biased Sampling): ↑ מתרחשת כאשר בוחרים או דּוֹגְמִים פריטים מאוסף של פריטים, כמו למשל זמנים ארוכים בין-אירועים או אדם עם חברים רבים, באופן תכוף יותר ביחס לפריטים אחרים, כתוצאה מכללי הבחירה.
הצהרת ניגוד אינטרסים
המחברים מצהירים כי המחקר נערך בהעדר כל קשר מסחרי או פיננסי שיכול להתפרש כניגוד אינטרסים פוטנציאלי.
תודות
אנו מודים לקוראים הצעירים שלנו - Nia Chiou, Taryn Chiou, Valerie E. Eng, Anthony Jin, Iris Leung, Maple Leung, Ami Masuda ו-Ritvik Mukherjee עבור הערותיהם המועילות הרבות. אנו גם מודים להוריהם ולמורים שלהם Lyndie- Chiou ו- Christina Chow – על שקישרו אותנו לקוראים הצעירים ועודדו את המשוב שלהם. אנו מבקשים להודות גם ל-Iris Leung על שציירה את איור 1A. תודתנו לקורא המעריך ולעורכים שלנו על הצעותיהם המועילות, ול- SocioPatterns collaboration (ראו http://www.sociopatterns.org) על סיפוק הנתונים. NM מודה על התמיכה מ- AFOSR European Office (מענק מספר FA9550-19-1-7024). MAP מודה על התמיכה מהקרן הלאומית למדעים (מענק מספר 1922952) דרך תוכנית Algorithms for Threat Detection (ATD).
מקורות
[1] ↑ Welding, P. I. 1957. The instability of a close-interval service. J. Oper. Res. Soc. 8:133–42. doi: 10.1057/jors.1957.21
[2] ↑ Masuda, N., and Hiraoka, T. 2020. Waiting-time paradox in 1922. Northeast J. Complex Syst. 2:1. doi: 10.22191/nejcs/vol2/iss1/1
[3] ↑ Isella, L., Romano, M., Barrat, A., Cattuto, C., Colizza, V., Van den Broeck, W., et al. 2011. Close encounters in a pediatric ward: Measuring face-to-face proximity and mixing patterns with wearable sensors. PLoS ONE 6:e17144. doi: 10.1371/journal.pone.0017144
[4] ↑ Feld, S. L. 1991. Why your friends have more friends than you do. Am. J. Sociol. 96:1464–77. doi: 10.1086/229693
[5] ↑ Strogatz, S. 2012. Friends You Can Count On. The New York Times. Available online at: https://opinionator.blogs.nytimes.com/2012/09/17/friends-you-can-count-on/
[6] ↑ Karsai, M., Kivelä, M., Pan, R. K., Kaski, K., Kertész, J., Barabási, A. L. et al. 2011. Small but slow world: how network topology and burstiness slow down spreading. Phys. Rev. E 83:025102(R). doi: 10.1103/PhysRevE.83.025102

